はじめに
建築や都市などの空間を考えるうえで、”距離”というのは大事な概念です。どこかへ移動するときには、なるべく短い距離で済ませたいものです。ただ、建物や地形を無視してまっすぐに移動するわけにはいかないので、それらをかわしながら移動する必要があります。移動経路があらかじめネットワーク(道路網、鉄道網、航空路網など)上に限定されていれば、そのネットワーク上の最短路を求めればよいことになります。このように、ネットワーク上の最短路を求めるアルゴリズムとして著名なのがDijkstra法1です。文字通りの距離だけでなく、どのように行けば速いかという時間距離や、安いかという金銭距離も、ネットワークの辺の重みの設定次第で求めることができます。
本稿では、Dijkstra法をPythonを用いて実装します。Dijkstra法は、動的計画法と呼ばれるアルゴリズム設計技法を利用した、非常にエレガントなアルゴリズムです。Dijkstra法がどのように動くのか、その仕組みにも触れながらコードの説明をします。とても勉強になるので、プログラミングにあまり触れてこなかった方にこそ、自分で実装してみることをおすすめします。
Dijkstra法
ネットワーク$ G(V, E) $を考えます。ここに、$ V $はネットワークの頂点、$ E $はネットワークの辺の集合で、$ e \in E $の長さは正とします。Dijkstra法は、ある頂点$ o \in V $から他の頂点までの最短路長を求める問題(単一始点最短路問題)の解法です。それでは、下図のようなネットワークについて、Dijkstra法の動き方について説明しましょう。$ o=0 $とします。
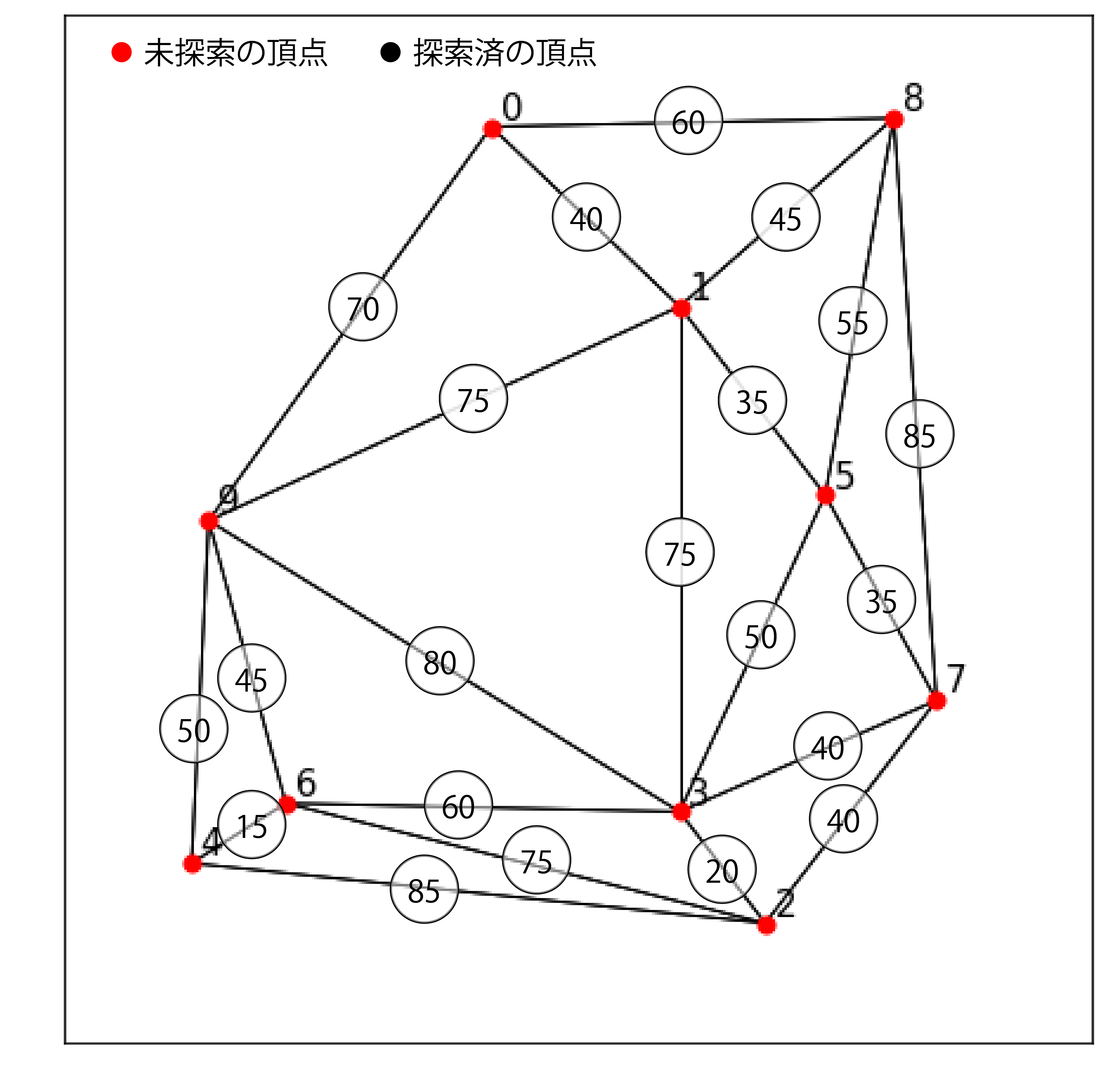
まず、未探索の頂点の集合$ Q $と、$ o $から$ v \in V $までの最短路長を格納しておく関数$ f(o, v) $を用意しておきます。それぞれ、$ Q=V $、$ f(o, v)=\infty $と初期化しておきます。$ o $から$ o $までの最短路長は$ 0 $なので、$ f(o, o)=0 $とします。

続いて、$ v \in Q $で、$ f(o, v) $が最小になる頂点、すなわち、$ o=0 $に接続する頂点の集合
U(0)= \{ 1, 8, 9 \}
を取り出します。この時点で$ o $から$ o $までの最短路長は確定しているので、$ Q $から$ o=0 $を除き探索済とします。$ U(0) $それぞれについて、$ f(0, v) $と$ f(0, 0)+|e(0, v)| $を比較し、$ f(0, v) $が$ f(0, 0)+|e(0, v)| $より大きい場合には、$ f(0, v) = f(0, 0)+|e(0, v)| $と更新します。この段階では、$ f(0, 1) = f(0, 8) = f(0, 9) = \infty $なので、$ U(0) $すべてで更新されます。

次に、$ v \in Q $で、$ f(o, v) $が最小になる頂点を取り出します。この場合、$ v=1 $です。$ v=1 $に接続する頂点の集合
U(1)= \{ 3, 5, 8, 9 \}
を取り出します($ v=0 $は探索済なので不要)。この時点で$ o $から$ v=1 $までの最短路長は確定している2ので、$ Q $から$ v=1 $を除き探索済とします。$ U(1) $それぞれについて、$ f(0, v) $と$ f(0, 1)+|e(1, v)| $を比較し、$ f(0, v) $が$ f(0, 1)+|e(1, v)| $より大きい場合には、$ f(0, v) = f(0, 1)+|e(1, v)| $と更新します。$ f(0, 3)=\infty , f(0, 1)+|e(1, 3)|=115 $、$ f(0, 5)=\infty , f(0, 1)+|e(1, 5)|=75 $、$ f(0, 8)=60, f(0, 1)+|e(1, 8)|=85 $、$ f(0, 9)=70, f(0, 1)+|e(1, 9)|=115 $なので、$ f(0, 3), f(0, 5) $が更新されます。

もう少し続けます。$ v \in Q $で、$ f(o, v) $が最小になる頂点は$ v=8 $です。$ v=8 $に接続する頂点の集合
U(8)= \{ 5, 7 \}
を取り出します($ v=0, 1 $は探索済なので不要)。この時点で$ o $から$ v=8 $までの最短路長は確定しているので、$ Q $から$ v=8 $を除き探索済とします。$ U(8) $それぞれについて、$ f(0, v) $と$ f(0, 8)+|e(8, v)| $を比較し、$ f(0, v) $が$ f(0, 8)+|e(8, v)| $より大きい場合には、$ f(0, v) = f(0, 8)+|e(8, v)| $と更新します。$ f(0, 5)=75 , f(0, 8)+|e(8, 5)|=115 $、$ f(0, 7)=\infty, f(0, 8)+|e(8, 7)|=145 $なので、$ f(0, 7) $が更新されます。

以上の操作を、$ Q=\emptyset $になるまで繰り返すと、$ o $から他の頂点までの最短路長がすべて求められます。

プログラムの実装
それでは、Dijkstra法を実際にプログラムしてみましょう。ネットワークのデータ形式は隣接配列です隣接配列です(→詳しくはこちら)。
# coding utf-8
import numpy as np
import heapq
def shortestpath_tree(neiList, nei_edge_len, orient):
"""
this function builds the shortest path tree rooted the orient by Dijkstra method
:param neiList: dictionary, neighborhood list
:param nei_edge_len: dictionary, distance list
:param orient: int, the index of the orient
:return:
"""
node_num = len(neiList)
Q = []
distance = [float("inf")] * node_num
previous_nodes = [-1] * node_num
distance[orient] = 0
for i in range(node_num):
heapq.heappush(Q, (distance[i], i)) # for fast finding of minimum
searched = set()
while len(searched) != node_num:
u = heapq.heappop(Q)
searched.add(u[1])
target_edge = nei_edge_len[u[1]]
for i, length in enumerate(target_edge):
if neiList[u[1]][i] in searched:
pass
else:
possible_min_distance = distance[u[1]] + length
if possible_min_distance < distance[neiList[u[1]][i]]:
distance[neiList[u[1]][i]] = possible_min_distance
previous_nodes[neiList[u[1]][i]] = u[1] # memorize the previous node of u[1] on the shortest path tree
heapq.heappush(Q, (distance[neiList[u[1]][i]], neiList[u[1]][i]))
return previous_nodes
def get_shortestpath(shortest_path_tree, destination):
"""
this func reads the shortest path tree backward
:param shortest_path_tree: list, return of shortestpath_tree()
:param destination: int, the index of the orient
:return:
"""
previous_node = destination
route = []
while previous_node != -1:
route.append(previous_node)
previous_node = shortest_path_tree[previous_node]
return route[::-1]
def get_path_length(path, neiList, nei_edge_len):
"""
this func calculate the total length of the path
:param path: list, return of get_shortestpath()
:param neiList: dictionary, neighborhood list
:param nei_edge_len: dictionary, distance list
:return:
"""
sp_l = 0.0
if len(path) == 1: # the orient and the destination are not connected
sp_l = float("inf")
else:
for i in range(len(path)-1):
start = path[i]
end = path[i+1]
l = nei_edge_len[start][neiList[start].index(end)]
sp_l += l
return sp_l
### network data ###
neiList = {0: [1, 8, 9],
1: [0, 3, 5, 8, 9],
2: [3, 4, 6, 7],
3: [1, 2, 5, 6, 7, 9],
4: [2, 6, 9],
5: [1, 3, 7, 8],
6: [2, 3, 4, 9],
7: [2, 3, 5, 8],
8: [0, 1, 5, 7],
9: [0, 1, 3, 4, 6]}
nei_edge_len = {0: [40, 60, 70],
1: [40, 75, 35, 45, 75],
2: [20, 85, 75, 40],
3: [75, 20, 50, 60, 40, 80],
4: [85, 15, 50],
5: [35, 50, 35, 55],
6: [75, 60, 15, 45],
7: [40, 40, 35, 85],
8: [60, 45, 55, 85],
9: [70, 75, 80, 50, 45]}
if __name__ == "__main__":
### Dijkstra method ###
# the shortest path tree
spt = shortestpath_tree(neiList, nei_edge_len, orient=0)
# the shortest path from 0 to 7
sp = get_shortestpath(spt, destination=7)
print("the shortest path from 0 to 7: ", sp)
# the length of the shortest path from 0 to 7
l = get_path_length(sp, neiList, nei_edge_len)
print("length: ", l)
shortestpath_tree()がDijkstra法の実装になります。少し解説すると、まず、$ f(o, v) $の最小値の検索を早めるためにヒープを用いています。また、返り値はそれぞれの頂点について、最短路のひとつ手前の頂点を格納した配列になります。この配列で目的地から順に頂点を追うことで、最短路を構成できます。この関数がget_shortestpath()です。そして、最短路の辺の長さをひとつずつ足し合わせれば最短路長が得られます。この関数がget_path_length()です。
以下は、実行結果です。
the shortest path from 0 to 7: [0, 1, 5, 7]
length: 110.0
おわりに
本稿では、Dijkstra法を実装しました。モジュールが公開されていたりもするので、自分で書かなくても実用上は問題ないのですが、Dijkstra法はアルゴリズムの何たるかに触れるのにいい題材だと思いますので、ぜひ、自分で書いてみてください。自分で書けると、細かい調整が効きますし、研究ではその方が都合がよいと思います。
一連の記事に関連するコードは、以下にあります。
→関連するコード
ホームページのご案内
建築・都市計画数理に関する私の研究の内容や、研究にまつわるtips等は、個人ホームページにて公開しています。ゆくゆくは、気軽に使える分析ツールも作っていきたいと思っているので、ぜひ覗きに来てください。
→田端祥太の個人ホームページ
参考文献・補注
-
Dijkstra, E. W. 1959. “A Note on Two Problems in Connexion with Graphs.” Numerische Mathematik. 1: 269–271. ↩
-
この点が、動的計画法らしさであり、Dijkstra法のミソです。始点から順番に最短路長を更新していくと、すべてのあり得る経路を列挙して長さを測り、それらを比較する必要がなくなります。Dijkstra法では、幾度となく「$ v \in Q $で、$ f(o, v) $が最小になる頂点を取り出」す操作があります。このとき、$ u \in Q $ \ {$ v $}を経由して$ v $に至る経路が最短路になることはありません。なぜなら、$ f(o, v) $は$ o $の周りから順に更新・確定されているため、$ v \in Q $で、$ f(o, v) $が最小になる頂点$ v $が取り出された段階で、どうあっても$ f(o, v)<f(o, u) $だからです。この論理が成り立つために、$ e \in E $の長さが正である必要があります。 ↩