はじめに
点同士を線で結び図式化することは、関係性を理解する上で有用です。昨今流行りのマインドマップもその一つでしょう。数理の世界では、定められたルールに基づいて点同士を結ぶことで、大量にある点を再現性を持って線で結ぶことを志向します。そのなかでも、距離にもとづいて点同士を直線分で結んだものを近接グラフと言います（近傍グラフ、幾何グラフとも）。
近接グラフは、「近い＝関係が深い」という考え方に基づいており、群れの形成を数理的に扱う際に、単一の群れを記述する方法として用いられたりします。また、筆者が属する建築・都市計画数理というフィールドでも、しばしば登場します。そこでは、「かつての都市においては、手段に乏しかったため、近いところへの移動ほど起こりやすかった」ことに起因する、都市空間に潜在する構造を、近接グラフの形状が浮き彫りにするという考えのもと、道路網形態の解析に用いられたりします。さらに、物理的な距離空間を超えて、データ間の類似度をもとにして構築されることもあり、データのクラスタリングや索引付けに応用されています。
このように、近接グラフの使い道はたくさんあるので、教科書的にそれぞれの定義や性質に関しては多くの情報があるのですが、それらをどうやって構築するのかに関する情報は、筆者が見た限り意外と少ないです。そこで本記事では、近接グラフを構築するプログラムをPythonで実装します。本記事によって、「近接グラフというものがあることは分かり、使ってみたが、どうやって作ったらいいかわからない」という人の役に立てば幸いです。
近接グラフの定義と関係
本記事では、近接グラフとしてドロネー網（Delaunay Triangulations、DT）、ガブリエルグラフ（Gabriel Graph、GG）、相対近傍グラフ（Relative Neighborhood Graph、RNG）、最小全域木（Minimum Spanning Tree、MST）を紹介し、その構築方法を実装します。これらの間には、とても便利な関係があります。それは、
MST \subset RNG \subset GG \subset DT
という関係です。それぞれの近接グラフの定義とともに、順番に説明しましょう。
ドロネー網
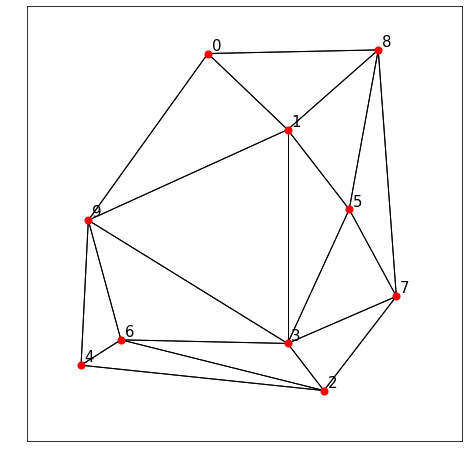ドロネー網は、ドロネー三角形分割の辺からなるグラフです。ドロネー網は、
- 3点の外接円の中に他の点を含まないような、すべての3点に対してそれぞれ三角形として結んだグラフ
- ボロノイ図の双対グラフ
と定義され、これらは同値です。
ガブリエルグラフ
ガブリエルグラフは、
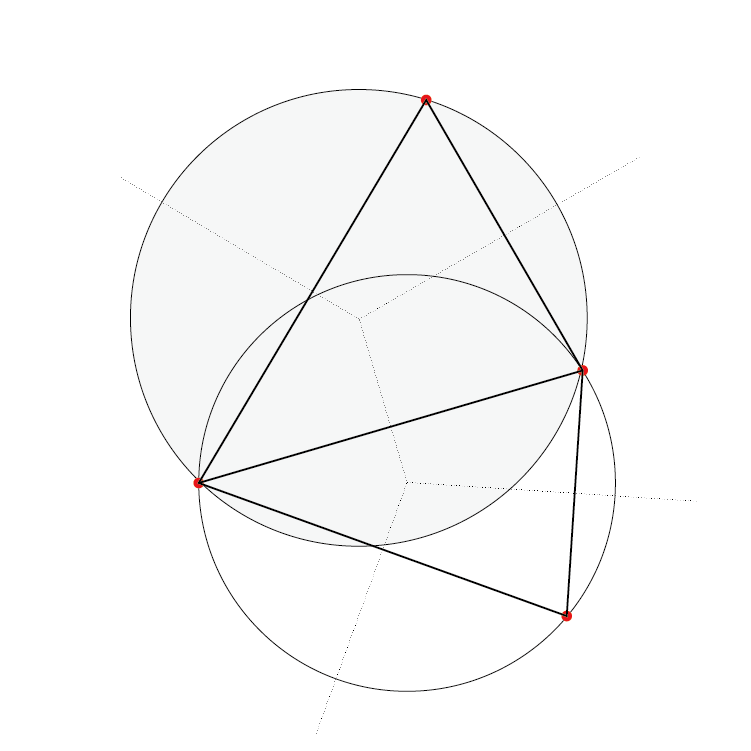
- 2点を結ぶ直線分を直径とする円の中に他の点を含まないような、すべての2点に対してそれらを結んだグラフ
と定義されます。
点$P_i$、$P_j$を結ぶ直線分を直径とする円に他の点が含まれないとき、$P_i$、$P_j$に接したまま円を連続的に変化させて、他の点$P_k$に接するように変形できます。このとき、$P_i$、$P_j$、$P_k$の外接円は中に他の点を含まず、これらの点を結んだ三角形の辺はドロネー網の辺になります。ということは、ガブリエルグラフの辺$P_iP_j$は、ドロネー網の辺でもある、すなわち、$GG \subset DT$となります。
相対近傍グラフ
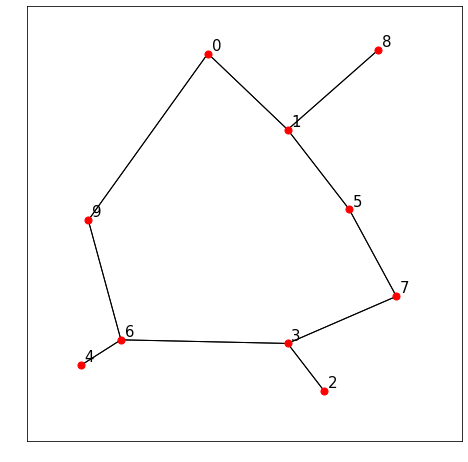相対近傍グラフは、
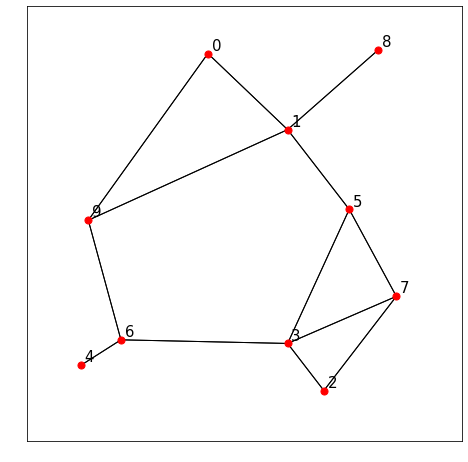
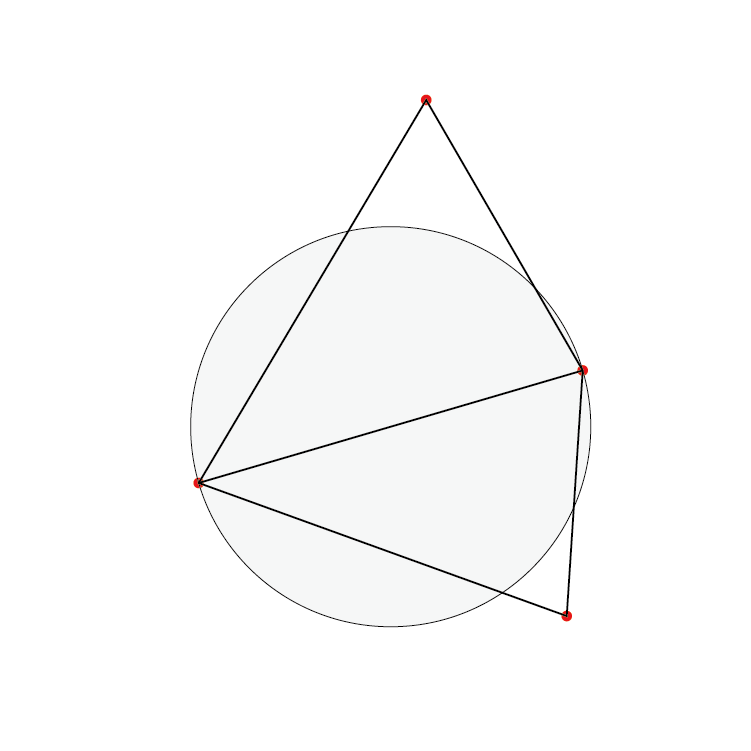
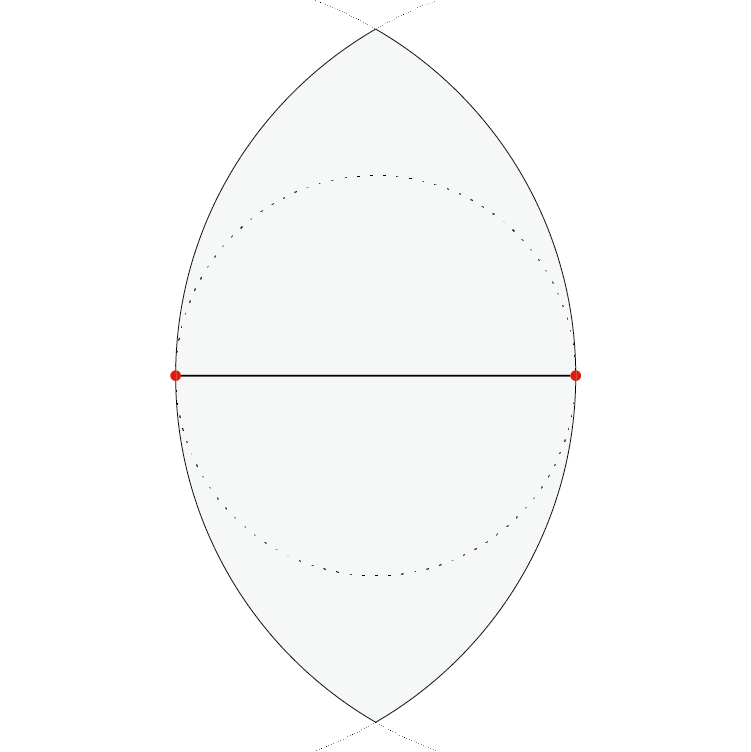
- 2点を結ぶ直線分を半径とし、それぞれの点を中心とする2つの円が重なる領域の中に他の点を含まないような、すべての2点に対してそれらを結んだグラフ
と定義されます。
点$P_i$、$P_j$が結ばれるために他の点が含まれてはいけない領域について、ガブリエルグラフのそれを相対近傍グラフのそれが含んでいるので、$RNG \subset GG$が成立します。
最小全域木
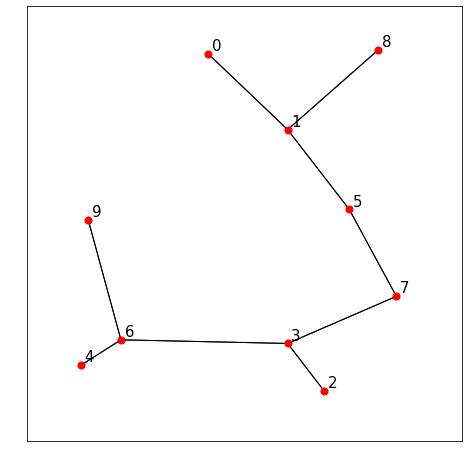最小全域木は、
- 2点を結ぶ直線分を辺とし、与点を連結するグラフの中で辺の総長が最小のもの
と定義されます。「連結する」とは、グラフをたどってどの点にも行けるということです。最小のグラフなので閉路は存在しません。なぜなら、閉路のいずれかの辺を切っても、連結は維持され、かつ、辺の総長を減らすことができるからです。閉路が存在しないグラフを「木」というので、最小全域木という名前になっています。
最小全域木は相対近傍グラフに含まれます。これを確かめるために、「最小全域木が相対近傍グラフに含まれない」と仮定しましょう。この過程に基づくと、最小全域木のある辺$P_iP_j$について、$P_iP_j$を半径とし、それぞれの点を中心とする2つの円が重なる領域の中に、他の点$P_k$があることになります。ここで、$P_iP_j$を切断し、$P_iP_k$を新しくつないで再び与点を連結しなおすことを考えると、$P_iP_j>P_iP_k$であるから、連結しなおしたグラフのほうが最小全域距離も小さくなります。これでは、最小全域木の定義に反するので、仮定は間違いであるということになります。したがって、$MST \subset RNG$が成立します。
プログラムの実装
近傍グラフの定義と、それらの関係について見てきましたが、$MST \subset RNG \subset GG \subset DT$という関係があることから、ドロネー網さえ求めてしまえば、ドロネー網の辺でガブリエルグラフの条件を満たしていないものを削除するだけでガブリエルグラフが構築でき、同様に相対近傍グラフ、最小全域木も構築することができます。これを踏まえて、Pythonで実装したものが以下になります。
# coding utf-8
import numpy as np
import copy
from scipy.spatial import Delaunay
import itertools
import heapq
"""
variable:
points: x-y coordination of points, like [[1.0, 2.5], [-2.7, 9.6], ...]
"""
class Graph:
def __init__(self):
self.adjacentList = None
self.lengthList = None
def getter(self, adjacentList, lengthList):
self.adjacentList = adjacentList
self.lengthList = lengthList
class Proximity_Graph:
def __init__(self, points):
self.points = points
self.DT = Graph()
self.GG = Graph()
self.RNG = Graph()
self.MST = Graph()
def all_activate(self):
self.get_DT()
self.get_GG()
self.get_RNG()
self.get_MST()
def get_DT(self):
if self.DT.adjacentList is None:
DT = Delaunay(self.points)
adjacentList = {}
for p in DT.vertices:
for i, j in itertools.combinations(p, 2):
try:
adjacentList[i].add(j)
except:
adjacentList[i] = {j}
# adjacentList[i].append(j)
try:
adjacentList[j].add(i)
except:
adjacentList[j] = {i}
# adjacentList[j].append(i)
adjacentList = dict(sorted(adjacentList.items()))
for k in adjacentList.keys():
adjacentList[k] = list(adjacentList[k])
lengthList = {}
for i in range(len(adjacentList)):
lens = []
for j in adjacentList[i]:
length = np.linalg.norm(np.array(self.points[i])-np.array(self.points[j]))
lens.append(length)
lengthList[i] = lens
self.DT.getter(adjacentList, lengthList)
return self.DT.adjacentList, self.DT.lengthList
def get_GG(self):
"""
Gabriel Graph:
considering the circle which diameter is the edge between point p and q,
it doesn't have other points than p and q.
FORTRAN 計算幾何プログラミング 杉原厚吉著 岩波書店 p 305
the edges of a Gabriel Graph are those of a Delaunay Triangulation
which cross the corresponding Voronoi edges.
only you have to check is whether r and s is in the circle or not
(r and s is the neighbor of both p and q).
"""
if self.GG.adjacentList is None:
DT_adjacentList, DT_lengthList = self.get_DT()
adjacentList = copy.deepcopy(DT_adjacentList)
lengthList = copy.deepcopy(DT_lengthList)
edges = set()
for k, v in adjacentList.items():
for u in v:
edge = tuple(sorted([k, u]))
edges.add(edge)
edges = list(edges)
for edge in edges:
p, q = edge # 2 end points
neighbors = set(self.DT.adjacentList[p]) & set(self.DT.adjacentList[q])
neighbors = list(neighbors)
invalidity = [np.dot((np.array(self.points[p])-np.array(self.points[r])),
(np.array(self.points[q])-np.array(self.points[r]))) <= 0.0 for r in neighbors]
if any(invalidity):
# delete edge pq
qi = adjacentList[p].index(q)
pi = adjacentList[q].index(p)
adjacentList[p].pop(qi)
lengthList[p].pop(qi)
adjacentList[q].pop(pi)
lengthList[q].pop(pi)
self.GG.getter(adjacentList, lengthList)
return self.GG.adjacentList, self.GG.lengthList
def get_RNG(self):
"""
Relative Neighbor Graphs
a relative neighbor graph consists of the edges which fulfill below,
d(p, q) <= min max{d(p, r), d(q, r)}.
FORTRAN 計算幾何プログラミング 杉原厚吉著 岩波書店 p 308
The Relative Neighborhood Graph of a Finite Planar Set, Toussaint G. T., Pattern Recognition vol. 12, pp. 261-268
"""
if self.RNG.adjacentList is None:
GG_adjacentList, GG_lengthList = self.get_GG()
adjacentList = copy.deepcopy(GG_adjacentList)
lengthList = copy.deepcopy(GG_lengthList)
edges = set()
for k, v in adjacentList.items():
for u in v:
edge = tuple(sorted([k, u]))
edges.add(edge)
edges = list(edges)
nodes = list(adjacentList.keys())
for edge in edges:
p, q = edge
length = lengthList[p][adjacentList[p].index(q)]
invalidity = [max(np.linalg.norm(np.array(self.points[p]) - np.array(self.points[r])),
np.linalg.norm(np.array(self.points[q]) - np.array(self.points[r]))) <= length
for r in nodes if r != p and r != q]
#print(edge)
#print(invalidity)
if any(invalidity):
# delete edge pq
qi = adjacentList[p].index(q)
pi = adjacentList[q].index(p)
adjacentList[p].pop(qi)
lengthList[p].pop(qi)
adjacentList[q].pop(pi)
lengthList[q].pop(pi)
self.RNG.getter(adjacentList, lengthList)
return self.RNG.adjacentList, self.RNG.lengthList
def get_MST(self):
"""
Minimum Spanning Trees
"""
if self.MST.adjacentList is None:
RNG_adjacentList, RNG_lengthList = self.get_RNG()
nodes = list(RNG_adjacentList.keys())
MST = kruskal(RNG_adjacentList, RNG_lengthList, nodes)
adjacentList = {}
lengthList = {}
for edge in MST:
p, q = edge
try:
adjacentList[p].append(q)
lengthList[p].append(RNG_lengthList[p][RNG_adjacentList[p].index(q)])
except KeyError:
adjacentList[p] = [q]
lengthList[p] = [RNG_lengthList[p][RNG_adjacentList[p].index(q)]]
try:
adjacentList[q].append(p)
lengthList[q].append(RNG_lengthList[q][RNG_adjacentList[q].index(p)])
except KeyError:
adjacentList[q] = [p]
lengthList[q] = [RNG_lengthList[q][RNG_adjacentList[q].index(p)]]
self.MST.getter(adjacentList, lengthList)
return self.MST.adjacentList, self.MST.lengthList
### Kruskal algorithm ###
def connection(target, linked_list, s1, s2):
"""
this updates the list of the sets of the points which is connected with each other
:param target: (point1.id, point2.id)
:param linked_list:
:param s1: sub graph which has point1
:param s2: sub graph which has point2
:return:
"""
if len(s1) == 0 and len(s2) == 0: # new sub graph
new_set = {target[0], target[1]}
linked_list.append(new_set)
elif len(s1) > 0 and len(s2) == 0: # point1 is already in a sub graph
linked_list.remove(s1)
s1.add(target[1])
linked_list.append(s1)
elif len(s1) == 0 and len(s2) > 0: # point2 is already in a sub graph
linked_list.remove(s2)
s2.add(target[0])
linked_list.append(s2)
else: # point1 and point2 is in different sub graphs. unite them
linked_list.remove(s1)
linked_list.remove(s2)
new_set = s1 | s2
linked_list.append(new_set)
return linked_list
def kruskal(adjacentList, lengthList, vertices):
"""
this builds the minimum spanning tree of terminals by Kruskal method
:param adjacentList: the adjacent list
:param lengthList: the length list
:param vertices: the list of vertices
:return:
"""
searched = set() # seached points
linked = [] # sets of linked points
mst = [] # branches of minimum spanning tree
mst_size = 0.0
Q = [] # length and a pair of points, which are sorted
t_n = len(vertices) # t_n is terminal number
for node1 in vertices:
for node2 in adjacentList[node1]:
heapq.heappush(Q, (lengthList[node1][adjacentList[node1].index(node2)], node1, node2))
# this is the first step of while
u = heapq.heappop(Q)
new_set = {u[1], u[2]}
linked.append(new_set)
mst.append(tuple(sorted([u[1], u[2]])))
searched.add(u[1])
searched.add(u[2])
c = True
while len(linked) != 1 or c:
u = heapq.heappop(Q)
set1 = set()
set2 = set()
continue_point = False
for s in linked:
if u[1] in s and u[2] in s: # both of u are already searched and linked
continue_point = True
break
else: # each of u must not be in some subgraphs.
if u[1] in s:
set1 = s
elif u[2] in s:
set2 = s
if continue_point:
continue
else:
mst.append(tuple(sorted([u[1], u[2]])))
t = (u[1], u[2])
linked = connection(t, linked, set1, set2)
searched.add(u[1])
searched.add(u[2])
if len(searched) == t_n:
c = False
return tuple(sorted(mst))
入力は与点の2次元座標のリストです。
それぞれのグラフは、隣接配列の形で記憶します（→詳しくはこちら）。それをGraphクラスに格納します。
それぞれの近接グラフはProximity_Graphクラスの中で構築されます。それぞれについて補足の説明をします。
get_DT()
ドロネー図を構築する関数です。アルゴリズムは多数存在していて、なかでも、「3次元凸包を投影する方法」や「与点を逐次的に加え辺を結びなおす方法」が有名でしょう。これらを1から実装するのは少し大変なのですが、Pythonのライブラリにscipy.spatial.Delaunayという便利なものがありますので、こちらを使わせていただきます。referenceを見ますと、どうやら前者のアルゴリズムで動いているようです。
前者のアルゴリズムに関しては、
・『FORTRAN 計算幾何プログラミング』、杉原厚吉著、岩波書店、pp. 11-16
後者のアルゴリズムに関しては、
・『Computational Geometry』、M. de Berg、M. van Kreveld、M. Overmars、O. Schwarzkopf著、Springer、pp. 189-194
・MIT - Delaunay Triangulations
が参考になるかと思います。
get_GG()
ガブリエルグラフを構築する関数です。先述の通り、ドロネー網の辺がガブリエルグラフの条件を満たしているかどうか調べるだけで構築できるので、まず、ドロネー網を先に作ります。
ガブリエルグラフの辺が満たすべき条件とは「その辺を直径とする円の中に他の点を含まない」ことでした。しかし、円の中に含まれるかどうかを、すべての点に対して確かめるのは大変です。そこで、少しドロネー網とガブリエルグラフを眺めてみると、円の中に含まれるかどうかを確かめればいいのは、注目している辺の両端点とドロネー網上で隣接している点だけだとわかります。それをinvalidityという変数に格納しています。
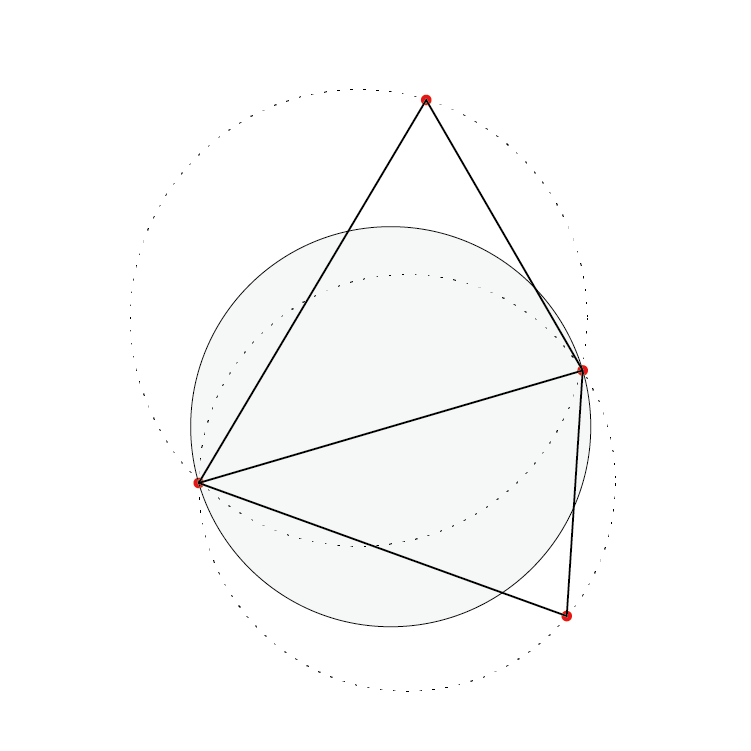
アルゴリズムの参考として、
・『FORTRAN 計算幾何プログラミング』、杉原厚吉著、岩波書店、pp. 303-305
が挙げられます。ここでは、ドロネー網の辺とボロノイ図の辺が交差するかどうかによって、ガブリエルグラフの辺が満たすべき条件を規定しています。
get_RNG()
相対近傍グラフを構築する関数です。先述の通り、ガブリエルグラフの辺が相対近傍グラフの条件を満たしているかどうか調べるだけで構築できるので、まず、ガブリエルグラフを先に作ります。
相対近傍グラフの辺が満たすべき条件を、注目している辺の周りの点についてだけ調べればよい、というような都合のいいことはなく、仕方がないので、すべての点に対して確かめます。
高速なアルゴリズムは、
・Kenneth J. Supowit, The Relative Neighborhood Graph with an Application to Minimum Spanning Trees, Journal of the Association for Computing Machinery, Volume 30, Number 3, 1983, Pages 428-448
・Andrzej Lingas, A linear-time construction of the relative neighborhood graph from the Delaunay triangulation, Computational Geometry, Volume 4, Issue 4, 1994, Pages 199-208
があります。
get_MST()
最小全域木を構築する関数です。先述の通り、相対近傍グラフは最小全域木を含むので、まず、相対近傍グラフを先に作ります。
最小全域木を構築する方法として有名なのがクラスカル法とプリム法です。本稿ではクラスカル法を実装しています。アルゴリズムはすごく単純で、相対近傍グラフの短い辺から、閉路ができないように足していくだけです。クラスカル法は別途kruskal()という関数で実装し、これによって最小全域木の辺の集合を得、改めて隣接配列に整理しています。
デモ
実装したアルゴリズムは、例えば、以下のようにして使うことができます。
points = [[0.4, 0.97], [0.62, 0.76], [0.72, 0.04], [0.62, 0.17], [0.05, 0.11], [0.79, 0.54], [0.16, 0.18], [0.92, 0.3], [0.87, 0.98], [0.07, 0.51]]
pg = Proximity_Graph(points)
pg.get_DT()
pg.get_GG()
pg.get_RNG()
pg.get_MST()
print("\nドロネー網")
print(pg.DT.adjacentList)
print("\nガブリエルグラフ")
print(pg.GG.adjacentList)
print("\n相対近傍グラフ")
print(pg.RNG.adjacentList)
print("\n最小全域木")
print(pg.MST.adjacentList)
出力は以下のようになります。点の座標、番号は先のものと同じです。隣接関係を正しく出力できていることが確認できます。
ドロネー網
{0: [8, 1, 9], 1: [0, 3, 5, 8, 9], 2: [3, 4, 6, 7], 3: [1, 2, 5, 6, 7, 9], 4: [9, 2, 6], 5: [8, 1, 3, 7], 6: [9, 2, 3, 4], 7: [8, 2, 3, 5], 8: [0, 1, 5, 7], 9: [0, 1, 3, 4, 6]}
ガブリエルグラフ
{0: [1, 9], 1: [0, 5, 8, 9], 2: [3, 7], 3: [2, 5, 6, 7], 4: [6], 5: [1, 3, 7], 6: [9, 3, 4], 7: [2, 3, 5], 8: [1], 9: [0, 1, 6]}
相対近傍グラフ
{0: [1, 9], 1: [0, 5, 8], 2: [3], 3: [2, 6, 7], 4: [6], 5: [1, 7], 6: [9, 3, 4], 7: [3, 5], 8: [1], 9: [0, 6]}
最小全域木
{0: [1], 1: [0, 5, 8], 5: [1, 7], 8: [1], 2: [3], 3: [2, 6, 7], 6: [3, 4, 9], 7: [3, 5], 4: [6], 9: [6]}
おわりに
本稿では、近接グラフの構築を実装しました。近接グラフの使い道はたくさんあるので、それらを有効活用したいときの手助けになれば幸いです。
一連の記事に関連するコードは、以下にあります。
→関連するコード
ホームページのご案内
建築・都市計画数理に関する私の研究の内容や、研究にまつわるtips等は、個人ホームページにて公開しています。ゆくゆくは、気軽に使える分析ツールも作っていきたいと思っているので、ぜひ覗きに来てください。
→田端祥太の個人ホームページ