はじめに
GWの連休中ふと思い立って「ゼロから作るDeep LearningーーPythonで学ぶディープラーニングの理論と実装」を手に取り勉強&実装してみたので、感想と自分なりの理解をメモ。
これから本書を手に取って勉強し始める人にとって、理解の手助けや学習コストをどの程度見込めばいいのかの参考になればなと思いますが、時間たった時に自分が見返して思い出すためのメモなので読みづらい部分もあるかもしれません。。。
細かい数式は参考書を見て詳しく追えばいいと思うので、ふわっと「Deep Learningってそういう仕組みなんだ」っていうふうに概要を分かった気になれればいいなと思いながら書いています。
自分は本書を一通り理解し、付属のサンプルコードを少し拡張することで、
"ペイント"で手書きした数字の画像ファイルの数字判別を行うシステムを作ることができました。
(※著作権の問題が絡んできそうなので、ソースコードは公開していません。)
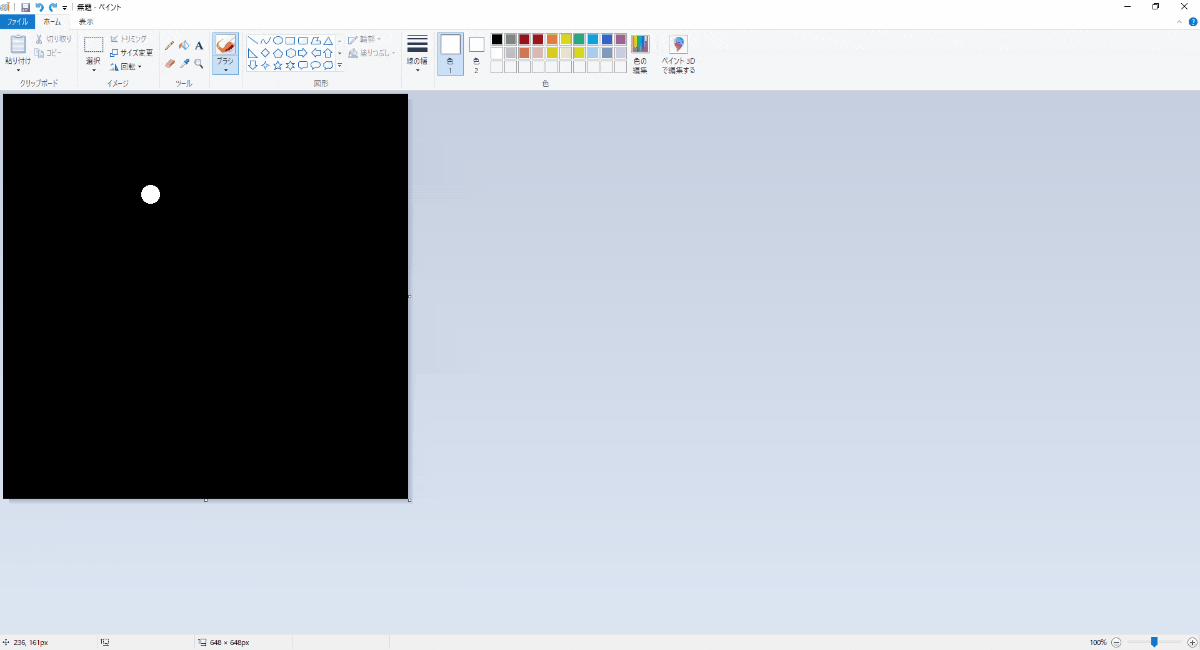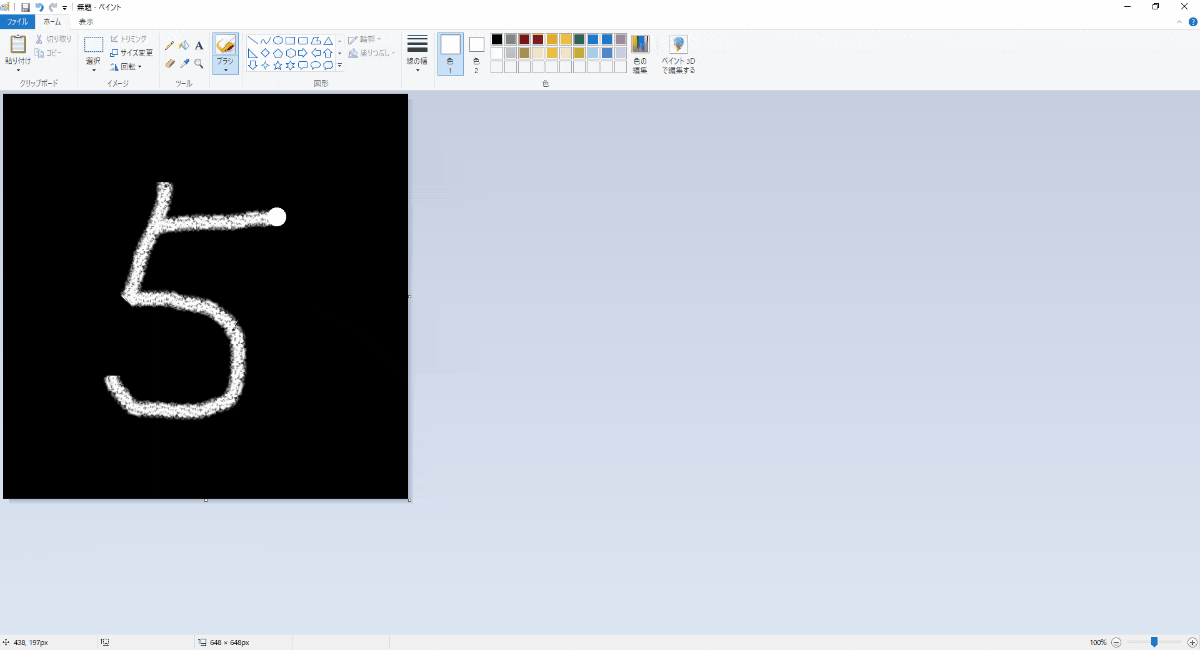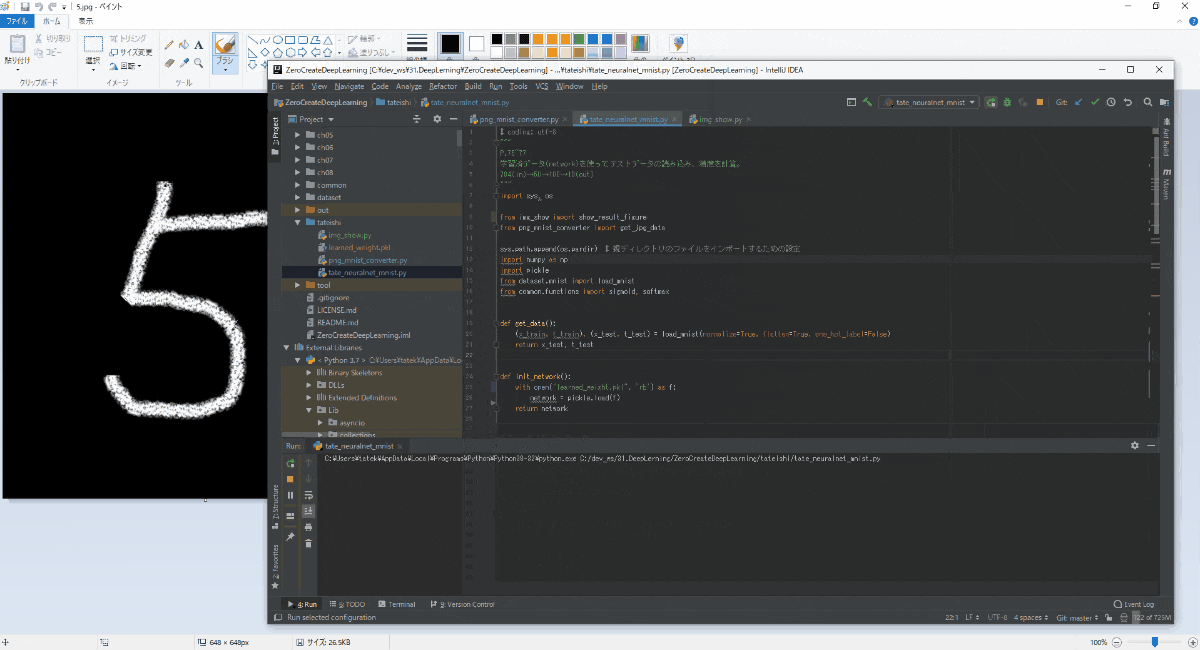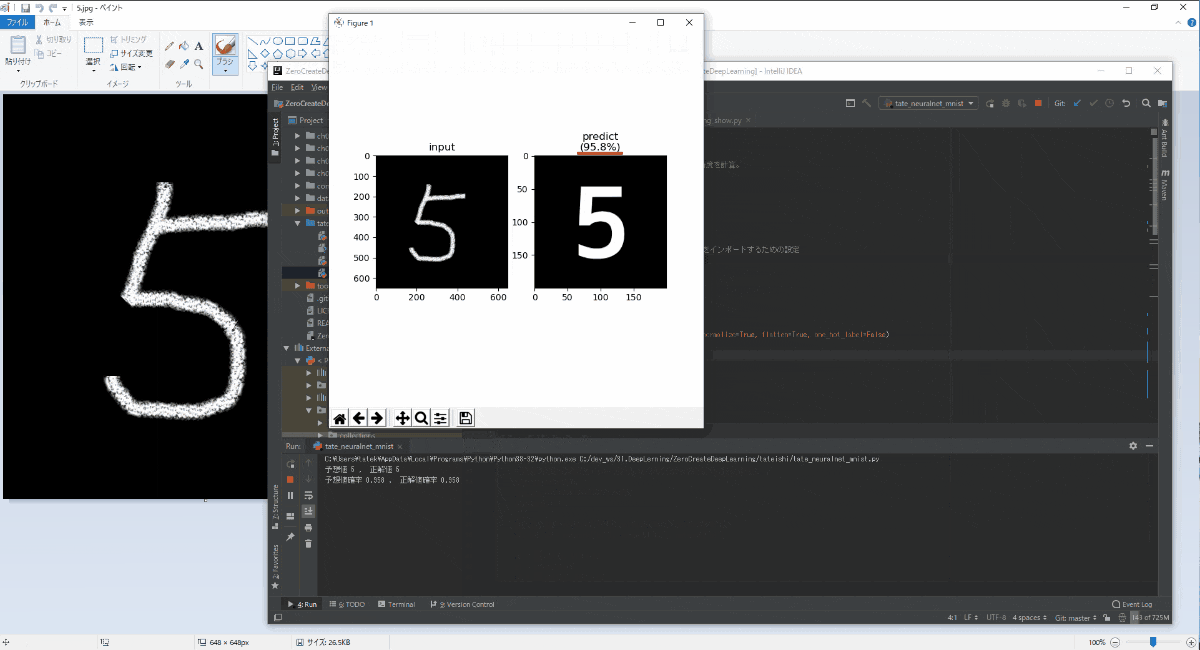
ざっくりDeep Learningについて
Deep Learningは「識別」と「学習」の機能のミックス。
それぞれを理解するためには、「入力値」、「ニューラルネットワークの関数」、「出力値」の3つの関係が重要。
-
「識別」とは、入力値と既知のニューラルネットワークの関数から出力値を求めること。(例: 何の数字かはわからない画像を読み込んで5だと認識する)
-
「学習」とは、正解(出力値)が既知であるテストデータ(入力値)からニューラルネットワークの関数を求めること。(例: 様々な手書きの数字の5の画像を読み込ませて、認識結果が5となるようにニューラルネットワークの関数をアップデートする)
なお、
「識別」の機能では__活性化関数__(2, 3章)、
「学習」の機能では__損失関数__、勾配降下法、__誤差逆伝播法__が重要であり(4, 5章)、
学習精度を高めるための工夫も様々ある(6, 7, 8章)。
「識別」機能について(2,3章)
前述した通り「識別」とは、入力値と既知のニューラルネットワークの関数から出力値を求めること。
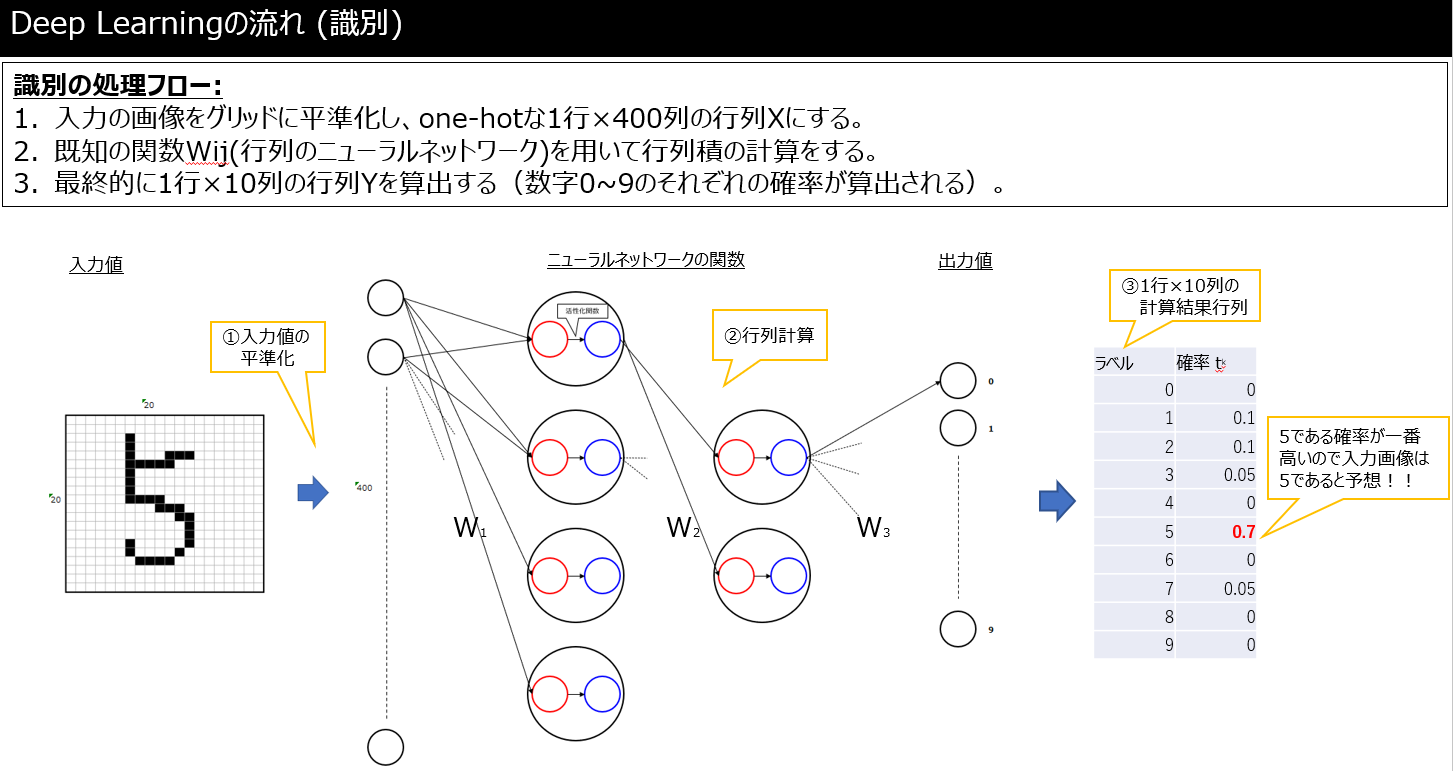
例として、何の数字かはわからない画像を読み込んで5だと認識するするフローについてはこんな感じ(下図も参照)。
- 何の数字かわからないけど読み込む画像について20×20のメッシュに切る(入力値)。
- 「ここのメッシュが黒塗りだったら数字XXの可能性が高い。」といった判断を下すような既知のニューラルネットワークの関数(所謂学習済データ)を用いる。(どうやって関数が定義されているかは「学習」で後述)
- 読み込んだ画像が数字0~9である確率をそれぞれ出す(出力値)。
 |
|---|
ここで大切なのは、この画像は「5だ!」のように断定しているのではなく、「5である確率が70%。なので5と思われる。」のように判断していて、出力値は1行10列の行列となるようにしていることです。
また、__活性化関数__を用いて出力された行列Yの「各要素が正の値になる」かつ「各要素の合計が"1"となる」とするよう工夫しており、代表的な関数としてはsigmoid関数やsoftmax関数がある。
「学習」機能について(4, 5章)
前述した通り「学習」とは、正解(出力値)が既知であるテストデータ(入力値)からニューラルネットワークの関数を求めること。
このニューラルネットワークの関数Wを__損失関数__、勾配降下法、__誤差逆伝播法__を用いて求めます。
 |
|---|
脱線:懐かしい高校数学
y = f(x)という関数において、入力値xと出力値yがわかっていれば、関数f(x)がわかるはず。
f(x) = ax^2 + bx + c
> 例えば2次関数のf(x)であれば、(x,y)の組み合わせが3通りあれば、a,b,cが求まり、f(x)が求まります。
それのちょっと難しくて行列のバージョンを「学習」でやっていると考えればよいわけです。
(高校数学が懐かしい:relaxed:)。
__損失関数__
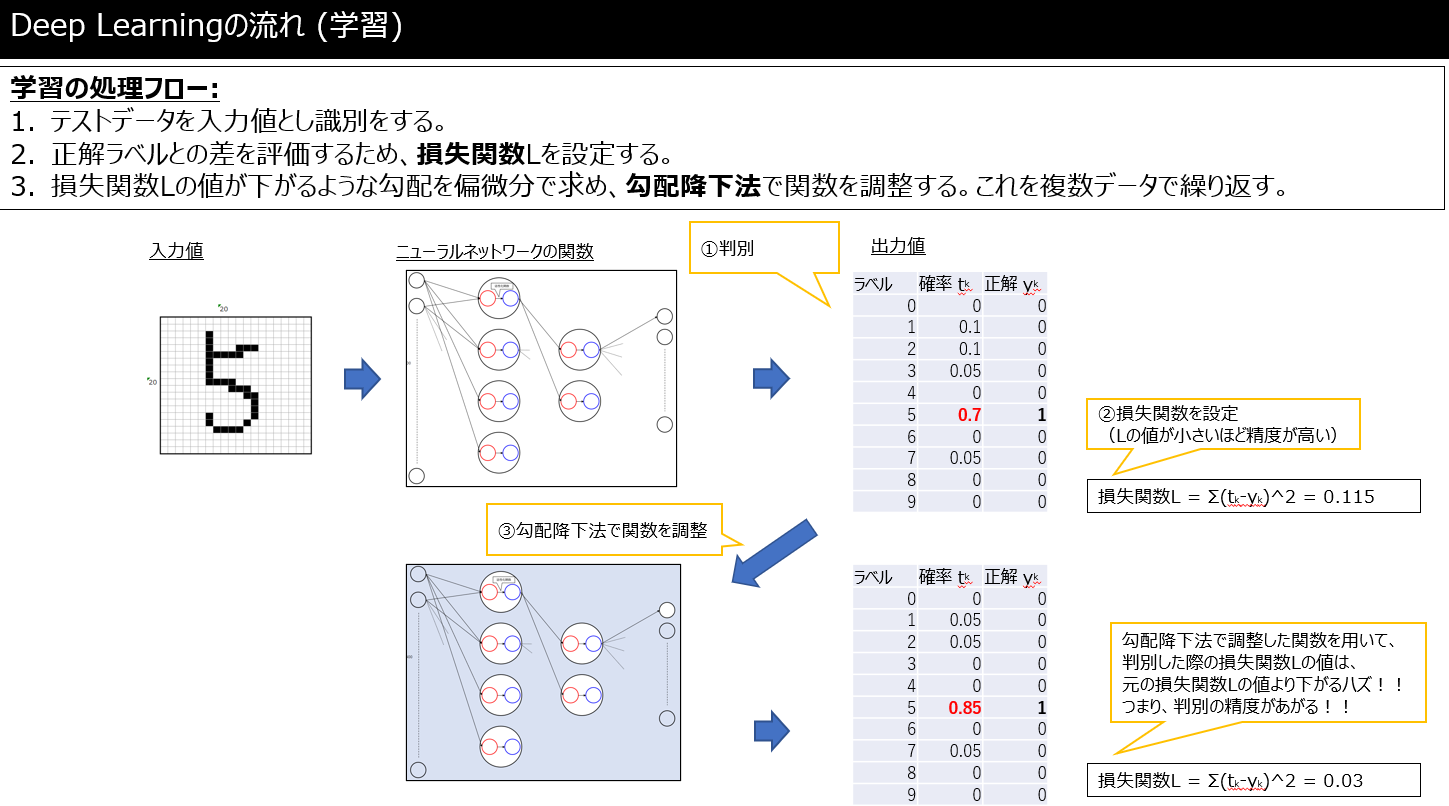
上の「Deep Learningの流れ(学習)」の図について、
- ニューラルネットワークの関数Aを用いると数字"5"である確率が0.7であった
- ニューラルネットワークの関数Bを用いると数字"5"である確率が0.85であった
といった場合に、どちらのニューラルネットワークの関数の方が__どの程度__優秀なのかを評価するための指標が損失関数Lです。
損失関数Lはエントロピー誤差とか2乗和誤差とかいろいろありますが、2乗和誤差の数式はコレ↓。
```math
L = \sum (X_{出力値}-X_{正解値})^2\\
ここで例えば、数字の画像を読み込んだ時の2~5の確率(出力値)が以下だった場合、それぞれのニューラルネットワークA,Bの損失関数Lは0.34, 0.14でニューラルネットワークの関数Bが優秀だとわかる。

また、当たり前ですが損失関数Lが0に近ければ近いほど正確に識別できているということであり、そのニューラルネットワーク関数Wを求めることが「学習」において重要ということです。
で、損失関数Lの値を小さくさせて(勾配降下法)関数Wを再計算します。
勾配降下法
現在の場所から勾配方向に一定の距離だけ進んだ場所のf(x)を求め、またその点から勾配方向に一定の距離ΔXだけ進んだ・・・というのを繰り返すことで極小値を求める手法。
2次元(下左図)であれば、X>極大値の任意の点(x,f(x))から始まれば、最終的に勾配法により極小値に落ち着く(勾配が0となる点が極小値)。
二乗和誤差の損失関数Lが3次元の場合(下左図)でも同様で、任意の点での勾配を求めて、勾配方向にΔXだけ進めるという操作を繰り返せば極小値にたどり着く。

n次元行列であっても偏微分することで極小値に向かう勾配が求まるので、勾配方向Δxだけずらしたものを出力値の行列Yとし、元の行列Xと子の行列Yからニューラルネットワークの関数Wを計算しなおすことで「学習」できる。
誤差逆伝播法
割愛。
まぁ偏微分と行列の特徴を抑えた計算が楽な手法。
学習精度を高めるための工夫(6, 7, 8章)
割愛。
減衰振動微分方程式とかも出てきて、ここから先はディープな世界です。。。
まとめ
今までの数学人生で遭遇したステージボスが全員集合して襲い掛かってきた感が凄いです。
どういうことかというと、
- 偏微分方程式(数ⅢC)
- n次元行列の行列積や転置(大学数学)
- 減衰振動微分方程式(院試)
など昔大学受験や大学在学中に苦労して勉強したなぁという内容のオンパレードで、Deep Learningについて学習する前にこれらを軽く思い出す必要がありました。
なのでプログラミングは強いけど、行列計算とか偏微分方程式はちょっと・・・という人には、やや学習コストが高くつく印象です。
ここまで読んでいただきありがとうございました。![]()