切断正規分布に従う乱数生成(Implement of Truncated Normal Distributiotion Random)

乱数に偏りを持たせたい場合、
例えば、
『能力値が平均的な物が多く出現するようなガチャを作りたい』
といった時は、中央を平均値とした正規乱数を作ればほぼ解決です。(ググれば結構出てくる)

では、『能力値が上位20%ぐらいに偏ったガチャを作りたい』
といった場合はどうでしょう。

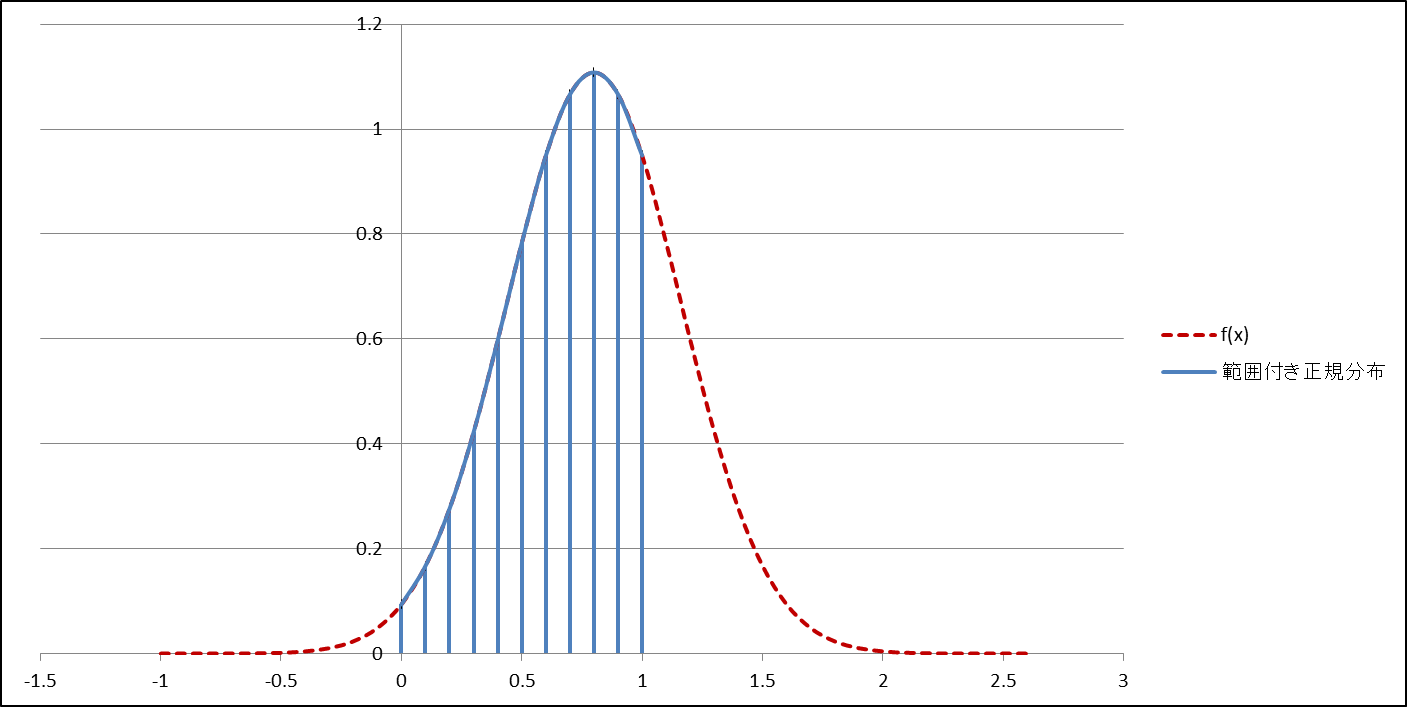
グラフは平均0.8 分散0.36の正規分布のグラフですが、
つまりは青い部分だけに分布するような乱数が欲しいわけです。
普通の正規分布だと、分散を大きくすればそれだけ点線部分の分布も多くなってきてしまいます。

範囲内のみを採用するという手もありますが、
分散が大きくなるほど、実装側では収束や処理時間の保証が難しくなってきます。

そこで今回は、範囲付きの正規分布、「切断正規分布」を用いて乱数を生成していきます。
https://ja.wikipedia.org/wiki/%E5%88%87%E6%96%AD%E6%AD%A3%E8%A6%8F%E5%88%86%E5%B8%83

これをC/C++での実装を解説しているサイトとか調べてもほとんど出てこなかったので、作りました。
ちなみにこの機能はC++11以上の環境では、既に搭載されていますし、
R言語など、GPLならばソースコードもあります。

なので、C++11なんて使える環境じゃないし、GPLなんて使えるか
っていう状況や、乱数は自前で行きたい人の参考になればと...
(多分R言語の手法とは違うはずです)
細かく説明を書いていますが、正規分布、正規乱数、一様乱数については理解しているものとします。

自分は数学のプロでも統計のプロでもないので、そこらへんの知識が浅いのはご容赦ください。

(訂正)
C++11の標準ライブラリでは正規乱数の範囲指定ができませんでした。訂正いたします。

切断正規分布の乱数の実現

切断正規分布は、正規分布に範囲をつけただけではありません。
範囲外の分が範囲内に計上されているはずなので、正規分布とは少し違ってくるのです。

Wikipediaを見ても・・・、何やら難しい式が書いてあって詳しい事はよく分かりませんが、
乱数は逆関数法を用いて導出することができます。
どうやら切断正規分布の乱数の定義は次のようになっているようです。

x = \phi^{-1}(\phi(\alpha) + U\times(\phi(\beta) - \phi(\alpha) )\sigma + \mu \\
(\alpha = \frac{a - \mu}{\sigma},\quad \beta = \frac{b - \mu}{\sigma})

a, bはそれぞれ切断正規分布の下限と上限、σは分散、μは平均となります。
Uは一様乱数、Φは標準正規分布の累積分布関数です。
(標準正規分布は、平均が0、分散が1の正規分布のことです。)
これを解けば乱数は実現できそうです。

標準正規分布の累積分布関数(CDF)

導出方法

標準正規分布の累積分布関数(Cumulative Distribution Function 略:CDF)
Φ(x)は、確率密度関数(Probability Density Function 略:PDF)のxまで累積です。
つまり、PDFをφとすると、

\phi(x) = \int_{-\infty}^{x}\varphi(t)dt

このように表すことができます。
これを実現することでCDFは作れます。

しかしこのままでは、不定積分ですので解くのは少し難しそうです。
ところが、標準正規分布の場合
x = 0の時、
Φ(0)=0.5となることが分かっています。

そのため、CDFの不定積分は、

\phi(x) = \begin{cases}
0.5 - \int_{x}^{0}\varphi(t)dt & ( x < 0 )\\
0.5 & ( x = 0 )\\
0.5 + \int_{0}^{x}\varphi(t)dt & ( x > 0 )
\end{cases}

このような定積分の式で表すことができます。
これで求めることが出来そうです。

標準正規分布の確率密度関数(PDF)の実装

標準正規分布のPDFは

\varphi(x) = \frac{e^{-\frac{x^{2}}{2}}}{\sqrt{2\pi}}

このように定義されています。

では実際これをプログラムで表現すると、

float StandardNormalPDF( float x )
{
    return expf( -0.5f * ( x * x ) ) / sqrtf( 2.0f * M_PI );
}

このようになります。

ガウス求積

定積分の近似計算のために、今回はガウス求積(ガウス・ルジャンドルの公式)を利用します。

詳しい原理は割愛しますが、今回の場合に当てはめると、φの定積分は、

\int_{a}^{b}\varphi(x)dx \approx \frac{b-a}{2}\sum_{i=1}^{n}w_{i}\varphi(\frac{b-a}{2}x_{i} + \frac{b+a}{2})

このようなN次の級数に変換できます。
wiはルジャンドル多項式の重み、xiがルジャンドル多項式の根です。
これらはそれぞれ定数として事前に定義しておくことができます。

/// ガウスノード(根)
static const float GaussNodeX[] =
{
    -9.931285e-1f,
    -9.639719e-1f,
    -9.122344e-1f,
    -8.391169e-1f,
    -7.463319e-1f,
    -6.360536e-1f,
    -5.108670e-1f,
    -3.737060e-1f,
    -2.277858e-1f,
    -7.652652e-2f,
     7.652652e-2f,
     2.277858e-1f,
     3.737060e-1f,
     5.108670e-1f,
     6.360536e-1f,
     7.463319e-1f,
     8.391169e-1f,
     9.122344e-1f,
     9.639719e-1f,
     9.931285e-1f,
};
/// ガウスノード(重み)
static const float GaussNodeW[] =
{
    1.761400e-2f,
    4.060142e-2f,
    6.267204e-2f,
    8.327674e-2f,
    1.019301e-1f,
    1.181945e-1f,
    1.316886e-1f,
    1.420961e-1f,
    1.491729e-1f,
    1.527533e-1f,
    1.527533e-1f,
    1.491729e-1f,
    1.420961e-1f,
    1.316886e-1f,
    1.181945e-1f,
    1.019301e-1f,
    8.327674e-2f,
    6.267204e-2f,
    4.060142e-2f,
    1.761400e-2f,
};

今回は最大で20次までとします。
ガウス求積をプログラムで表現すると次のようになります。

float GetGaussianIntegral( float a, float b, float( *func )( float ), uint32_t degree = 20 )
{
    if( func == NULL ){
        DEBUG_ASSERT( false, "[%s]求積できません\n", __FUNCTION__ );
        return 0.0f;
    }
    float center = ( b - a ) * 0.5f;
    float integral = 0.0f;
    const uint32_t N = ( degree <= NUMBEROF( GaussNodeW ) && degree <= NUMBEROF( GaussNodeX ) ) ? degree : static_cast<uint32_t>( fminf( NUMBEROF( GaussNodeW ), NUMBEROF( GaussNodeX ) ) );
    for( uint32_t i = 0; i < N; ++i ){
        integral += GaussNodeW[i] * func( ( center * GaussNodeX[i] ) + ( ( b + a ) * 0.5f ) );
    }
    return center * integral;
}

DEBUG_ASSERTはassert, NUMBEROFは配列の要素数を表すマクロです。
被積分関数を関数ポインタで引数にしていますが、そこは臨機応変に・・・。

Nを大きくすればするほど精度は高くなります。
ただし、標準正規分布のPDFにおいて発生するかどうかは未確認ですが、
Nを大きくすると、ルンゲ現象が発生し、まったく信頼できる値ではなくなってしまいます。
今回は大丈夫ですが、万能ではないようです。

CDFの実現

不定積分も、PDFも導出することができるようになったので、改めてCDFをプログラムで表すと次のようになります。

float StandardNormalCDF( float x )
{
    float ORIGINAL_POINT = 0.5f;
    if( x > 0.0f ){
        return ORIGINAL_POINT + GetGaussianIntegral( 0.0f, x, StandardNormalPDF, 20 );
    }
    else if( x < 0.0f ){
        return ORIGINAL_POINT - GetGaussianIntegral( x, 0.0f, StandardNormalPDF, 20 );
    }
    return ORIGINAL_POINT;
}

標準正規分布の逆累積分布関数

相補累積分布関数(CCDF)

定義に出現してきたΦ^-1は、CDFの逆関数(逆累積分布関数)です。
これを求めるためには、標準正規分布の相補累積分布関数(Complementary Cumulative Distribution Function 略:CCDF)を利用します。

CCDFはCDFとの合計が1となるような関数のことです。
つまり、CDFをF(x)、 CCDFをG(x)とすると、次のような関係が成り立ちます。

p = F(x)\\
F(x) + G(x) = 1\\
x = F^{-1}(p) = G^{-1}(1-p)

また、正規分布の累積分布関数のグラフを見ると、

グラフは、(x, Φ(x)) = (0, 0.5)を中心として、上下左右対称となっていることが分かります。
つまり、xが負の場合のCDFの値は正方向のCCDFの値と同等となっているのです。
よって、

p = F(x) = G(-x)\\
x = F^{-1}(p) = -G^{-1}(p)

このような関係が成り立ちます。

逆累積分布関数は、CCDFの逆関数によって表すこともできるようです。

CCDFの有理近似公式

Abramowitz and Stegunによると、

p = G(x_{p})

で表される標準正規分布のCCDFにおいて、
0 < p ≦ 0.5
ならば、

x_{p} = t - \frac{c_{0} + c_{1}t + c_{2}t^2}{1 + d_1t + d_2t^2 + d_3t^3} + \epsilon(p)\\
t = \sqrt{log\frac{1}{p^2}}\\
c_0 = 2.515517 \quad c_1 = 0.802853 \quad c_2 = 0.010328\\
d_1 = 1.432788 \quad d_2 = 0.189269 \quad d_3 = 0.001308\\
|\epsilon(p)| < 4.5 \times 10^{-4}

このように表すことができると言います。
ここで、誤差であるε(p)は、10^-4と、非常に小さい値となりほぼ無視できるので、
これを使うことで、CCDFの逆関数の有理近似を得ることができます。

これをプログラムで表すと次のようになります。

float GetRationalApproximation( float p )
{
    const float c[] = { 2.515517f, 0.802853f, 0.010328f };
    const float d[] = { 1.432788f, 0.189269f, 0.001308f };
    float t = sqrtf( -2.0f * logf( p ) );
    //  ホーナー法によって公式を最適化
    return t - ( ( c[2] * t + c[1] ) * t + c[0] ) / ( ( ( d[2] * t + d[1] ) * t + d[0] ) * t + 1.0f );
}

多項式は、ホーナー法によって変形することで計算回数を減らします。

逆CDFの実現

前述の近似公式には、適用される範囲があります。
0 < p ≦ 0.5
です。
実際のpが取りうる範囲は0 < p < 1ですので、0.5 < p < 1の場合を求める必要があります。
0 < p < 1なので、p > 0.5の場合は、p'=1-pとすれば、0 < p' ≦ 0.5となり公式に当てはめることが可能となります。
そこで、前述のCDFとCCDFの関係から、CDFの逆関数は次のように表すことができます。

x = \begin{cases}
-G^{-1}(p) & ( 0 < p \leq 0.5 )\\
G^{-1}(1 - p) & ( 0.5 < p < 1 )
\end{cases}

この関係から、有理近似公式に当てはめることで、逆CDFを実現できます。
これらを踏まえた上で、逆CDFをプログラムで表現すると次のようになります。

float StandardNormalCDFInverse( float x )
{
    if( x <= 0.0f ){
        DEBUG_ASSERT( false, "[%s]求められません\n", __FUNCTION__ );
        return -FLT_MAX;
    }
    else if( x >= 1.0f ){
        DEBUG_ASSERT( false, "[%s]求められません\n", __FUNCTION__ );
        return FLT_MAX;
    }
    return ( x < 0.5f ) ? -1.0f * GetRationalApproximation( x ) : GetRationalApproximation( 1.0f - x );
}

グラフを見ると分かりますが、x≦0やx≧1では、結果は±∞に発散してしまいますので注意。

切断正規分布の乱数の実装

必要な要素が全て揃いましたので

x = \phi^{-1}(\phi(\alpha) + U\times(\phi(\beta) - \phi(\alpha) )\sigma + \mu \\
(\alpha = \frac{a - \mu}{\sigma},\quad \beta = \frac{b - \mu}{\sigma})

この定義をプログラムで表してみましょう。

float RandTruncatedNormal( float a, float b, float mu, float sigma )
{
    float alpha = ( a - mu ) / sigma;
    float beta = ( b - mu ) / sigma;
    return StandardNormalCDFInverse( StandardNormalCDF( alpha ) + ( RandF() * ( StandardNormalCDF( beta ) - StandardNormalCDF( alpha ) ) ) ) * sigma + mu;
}

実際は例外処理などが含まれますが、ここでは省略しています。(a, b, sigmaの値が異常なケースなど)

RandF()は0 < u < 1の範囲の一様乱数を取得する関数です。
色々な方法があると思いますが、自分はXorshiftで作っています。
Xorshiftの実装方法はググればすぐ出てくるのでここでは書きません。

結果

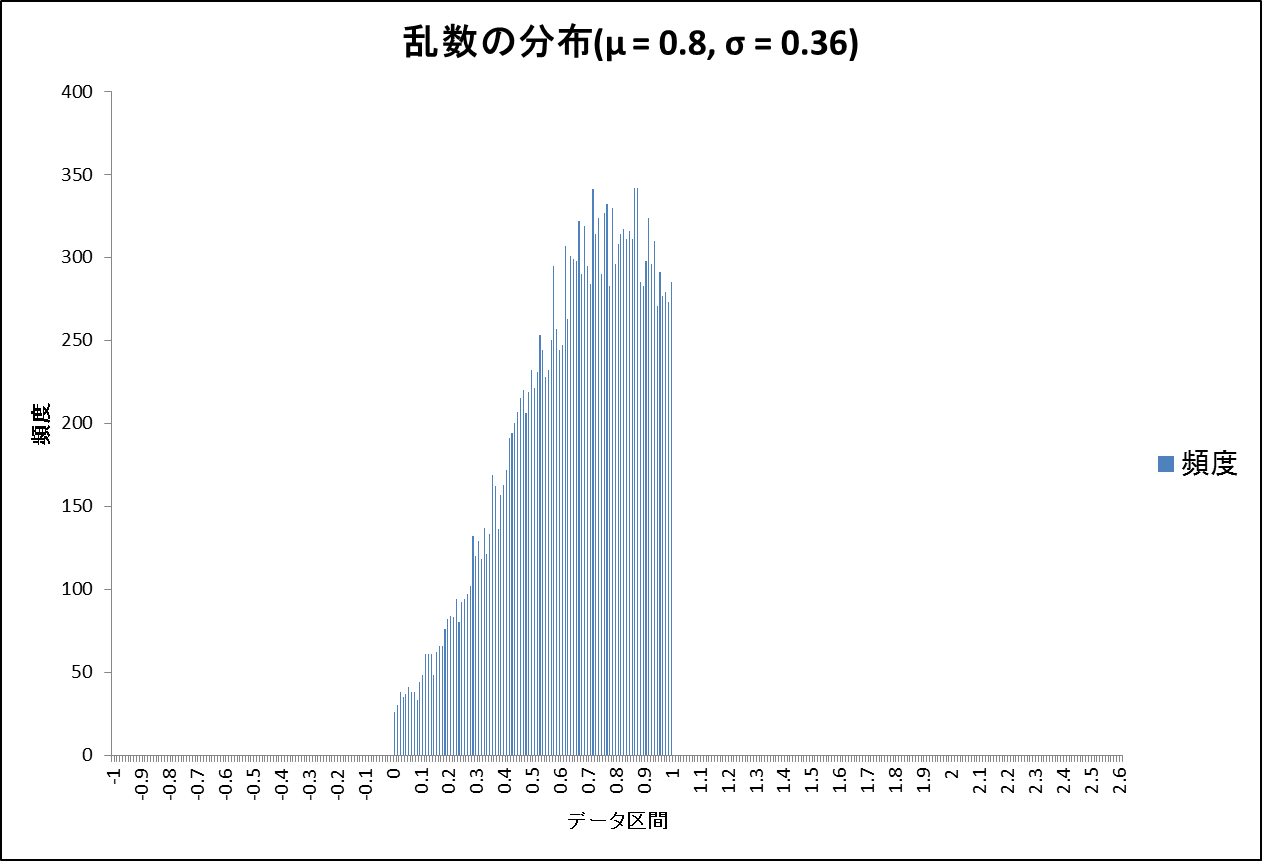
下限を0、上限を1、平均を0.8、分散を0.36として
乱数生成を20000回行った時の乱数の分布は次のようになりました。

0から1の区間に限定され、0.8付近が最も多くなる正規分布曲線となっていることが分かります。
少しデコボコしていますが、これぐらいならガチャのようなケースでは問題なさそうです。
処理時間もかなり短いです。(実測はしていませんが)

今回はゲームのような高いリアルタイム性を想定し、高速さも意識していますが、
速度よりも精度を重視したい場合などは、
ガウス求積の次数を大きくしたり、floatではなくdoubleを使ったり、Xorshiftではなくメルセンヌツイスタを使ったりと、
色々と応用が利きます。

参考サイト

• Truncated normal distribution - Wikipedia
• Normal distribution - Wikipedia
• 正規分布の確率計算：C++/Linuxプログラム
• ガウス･ルジャンドル積分
• Normal distribution inverse