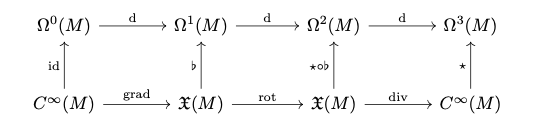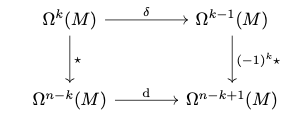Hodge starを目指して

\def\pdv#1#2{\frac{\partial #1}{\partial #2}}
\def\dd#1{\mathrm{d}#1}
\def\sgn{\mathrm{sgn}}
\def\vbud#1#2#3{#1^{#2}{}_{#3}}
\def\vbdu#1#2#3{#1_{#2}{}^{#3}}
\def\onf#1{\hat{\theta}^{#1}}
\def\abs#1{\lvert #1 \rvert}
\def\pair#1#2{\langle #1,\, #2 \rangle}

この記事は 理物 Advent Calendar 2022 の14日目の記事です。

はじめに

こんばんは，物理学科3年の T.T. です．微分形式を布教すべく記事を書こうと思い立ったのですが，話したい内容に辿り着くまでに必要な準備が思っていたより遥かに多く，午前中に投稿するつもりが気がついたら夜になってしまいました．
この記事の到達目標は，外微分とHodge starを利用して一般曲線座標（必ずしも直交していない）におけるスカラー関数の勾配，ラプラシアン，およびベクトル場の回転，発散を積の微分や連鎖律を使うことなく求める方法を紹介することですが，テンソル場，および微分形式の構成法についても軽く触れてあります．できるだけ全体像が掴みやすいような構成にしたつもりですが，その代償として数学的厳密性が完全に犠牲となっておりますので，話半分程度に流し読みする程度に扱ってやってください．きっちりと議論したい方には，参考文献 で紹介する Lee (2012) をお勧めします．

微分幾何学の基本的なあれこれ

本記事で扱う多様体は全て $C^\infty$ 多様体とします．多様体 $M$ 上の $C^\infty$ 級関数（$f\colon M \to \mathbb{R}$ という形をしているもの）全体の集合を $C^\infty(M)$，$M$ 上のベクトル場全体の集合を $\mathfrak{X}(M)$ と書きます．また，多様体 $M$ の局所座標系（またはチャート）を $(U,\, \varphi) = (U;\, x^1,\, \dots,\, x^{\dim M})$ などと書き，1点 $p \in M$ における接空間 (tangent space) を $T_p M$ と書きます．$T_pM$ は

    v \colon C^\infty(M) \longrightarrow \mathbb{R}

という形をした写像のうち$\forall f,\, g \in C^\infty(M),\; \forall \lambda \in \mathbb{R}$ に対して

1. 線型性を充たす：

    v(f + g) = v(f) + v(g),\quad v(\lambda f) = \lambda v(f)

1. Leibniz則を充たす：

 v(fg) = v(f)\, g(p) + f(p)\, v(g)

ようなもの全体の集合で，和とスカラー倍がそれぞれ

    (v+w)(f) := v(f) + w(f),\quad (\lambda v)(f) := \lambda v(f)

と定義された $\mathbb{R}$ ベクトル空間です．

$p \in U$ なるチャート $(U,\, \varphi) = (U;\, x^1,\, \dots ,\, x^d)$ を取ったとき，$T_p M$ の基底

    \left(\pdv{}{x^1}\right)_p,\; \left(\pdv{}{x^2}\right)_p ,\, \dots,\, \left(\pdv{}{x^d}\right)_p

のことを自然基底と呼びます．正確には

    \left(\pdv{}{x^\mu}\right)_p \colon C^\infty(M) \longrightarrow \mathbb{R},\; f \longmapsto \pdv{}{x^\mu}(f \circ \varphi^{-1})(\varphi(p))

ということなのですが，かえってわかりにくくなってしまうので原則

    \pdv{}{x^\mu},\quad \partial_\mu

などと略記します．

また，なんの断りもなくEinsteinの規約を用いることがあります．これは，上付きの添字と下付きの添字が揃っていたら和をとると言うものです：

A_\mu B^\mu := \sum_{\mu} A_\mu B^\mu

ベクトル解析に現れるベクトル場

突然ですが，3次元極座標系を考えます．

\boldsymbol{r}(r,\, \theta,\, \phi) 
=
\begin{bmatrix}
    r \sin \theta \cos \phi \\
    r \sin \theta \sin \phi \\
    r \cos \theta
\end{bmatrix}

古典力学や古典電磁気学などで登場するベクトル場というと，3次元極座標系に対応する正規直交基底

\boldsymbol{e}_r = 
\begin{bmatrix}
    \sin \theta \cos \phi \\
    \sin \theta \sin \phi \\
    \cos \theta
\end{bmatrix}, \quad
\boldsymbol{e}_\theta = 
\begin{bmatrix}
    \cos \theta \cos \phi \\
    \cos \theta \sin \phi \\
    -\sin \theta
\end{bmatrix}, \quad
\boldsymbol{e}_\phi = 
\begin{bmatrix}
    -\sin \phi \\
    \cos \phi \\
    0
\end{bmatrix}

をとって，

    \boldsymbol{F} = F^r \boldsymbol{e}_r + F^\theta \boldsymbol{e}_\theta + F^\phi \boldsymbol{e}_\phi

と成分表示したものを指すことが多いと思います．3次元空間 $\mathbb{R}^3$ の各点 $p \in \mathbb{R}^3$ に3次元ベクトル空間 $T_p \mathbb{R}^3 = \mathbb{R}^3$ が生えていて，$\boldsymbol{F} \in T_p\mathbb{R}^3$ となっているイメージです．こうすると3次元空間に具体的に絵を書くことができるので分かりやすい気がします．

ところで，$\boldsymbol{e}_{r},, \boldsymbol{e}_{\theta},\, \boldsymbol{e}_{\phi}$ を観察すると

    \frac{\partial \boldsymbol{r}}{\partial r} = \boldsymbol{e}_r,\quad
    \frac{\partial \boldsymbol{r}}{\partial \theta} = r\boldsymbol{e}_\theta,\quad
    \frac{\partial \boldsymbol{r}}{\partial \phi} = r \sin\theta \boldsymbol{e}_\phi

の関係があることがわかります．空間内の一点 $p = (r,\, \theta,\, \phi)$ を固定すると $r$ とか $r \sin \theta$ は定数と思えるので，点 $p$ におけるベクトル空間 $T_p\mathbb{R}^3$ の基底には $\frac{\partial \boldsymbol{r}}{\partial r},\, \frac{\partial \boldsymbol{r}}{\partial \theta},\, \frac{\partial \boldsymbol{r}}{\partial \phi}$ を採用しても良いはずです．このとき，ひとまず $\tilde{F}^r := F^r,\; \tilde{F}^\theta := F^r/r,\; \tilde{F}^r := F^r/r\sin\theta$ とおくと

    \boldsymbol{F} = 
    \tilde{F}^r \frac{\partial \boldsymbol{r}}{\partial r} + 
    \tilde{F}^\theta \frac{\partial \boldsymbol{r}}{\partial \theta} + 
    \tilde{F}^\phi \frac{\partial \boldsymbol{r}}{\partial \phi}

と書けます．とっても多様体の接空間の自然基底に似ていますね．実際，連鎖律から $\forall f \in C^\infty(\mathbb{R}_+\times S^2)$ に対する自然基底の作用は

\begin{align}
\frac{\partial}{\partial r} (f) &= \frac{\partial \boldsymbol{r}}{\partial r} \cdot  \frac{\partial f}{\partial \boldsymbol{r}} \\
\frac{\partial}{\partial \theta} (f) &= \frac{\partial \boldsymbol{r}}{\partial \theta} \cdot  \frac{\partial f}{\partial \boldsymbol{r}} \\
\frac{\partial}{\partial \phi} (f) &= \frac{\partial \boldsymbol{r}}{\partial \phi} \cdot  \frac{\partial f}{\partial \boldsymbol{r}}
\end{align}

と書けるので，$\frac{\partial}{\partial r}$ と $\frac{\partial \boldsymbol{r}}{\partial r}$，$\frac{\partial}{\partial \theta}$ と $\frac{\partial \boldsymbol{r}}{\partial \theta}$，$\frac{\partial}{\partial \phi}$ と $\frac{\partial \boldsymbol{r}}{\partial \phi}$ を同一視できます．つまり，我々が古典論でベクトル場と呼んでいたものは左 $C^\infty \bigl(\mathbb{R}_+\times S^2\bigr)$ 加群 $\mathfrak{X} \bigl(\mathbb{R}_+\times S^2\bigr)$ の元

    \boldsymbol{F} = \tilde{F}^r \frac{\partial}{\partial r} + 
    \tilde{F}^\theta \frac{\partial}{\partial \theta} + 
    \tilde{F}^\phi \frac{\partial}{\partial \phi} 
    \in \mathfrak{X} \bigl(\mathbb{R}_+\times S^2\bigr)

だったのです（先程は多様体上の一点 $p$ に固定していましたが，$p$ を $\mathbb{R}_+\times S^2$ 全域で動かすと $\tilde{F}^r,\, \tilde{F}^\theta,\, \tilde{F}^\phi \in C^\infty \bigl(\mathbb{R}_+\times S^2\bigr)$ になります）．

Euclid空間への埋め込み

先述の事柄を抽象的に見てみましょう．まずEuclid空間 $\mathbb{R}^3$ 内の「位置ベクトル」 $\boldsymbol{r}(r,\, \theta,\, \phi)$ がありましたが，これは次のような写像であると考えられます：

    \boldsymbol{r} \colon \mathbb{R}_+ \times S^2 \longrightarrow \mathbb{R}^3

より直接的に言うと，先程書き下した位置ベクトル $\boldsymbol{r}(r,\, \theta,\, \phi)$ は多様体 $\mathbb{R}_+ \times S^2$ の局所座標系を $(U,\, \varphi)$，多様体 $\mathbb{R}^3$ の局所座標系を $(V,\, \psi)$ とおいた時に写像

    \psi \circ \boldsymbol{r} \circ \varphi^{-1} \colon \mathbb{R}^3 \longrightarrow \mathbb{R}^3,\; (r,\, \theta,\, \phi) \longmapsto (x,\, y,\, z)

を与えていたことになります．表面的には単に $\mathbb{R}^3 \longrightarrow \mathbb{R}^3$ の対応になっているため，背景にある $\mathbb{R}_+ \times S^2 \longrightarrow \mathbb{R}^3$ の対応を意識しなくても色々と計算できていたわけです．しかし，$\mathbb{R}^3 \longrightarrow \mathbb{R}^3$ の対応は座標系の取り方に大きく依存する，i.e. 関数 $\psi \circ \boldsymbol{r} \circ \varphi^{-1}$ は多様体の局所座標系の取り方によってその具体形を変えてしまい全然共変じゃないので，物理的にも幾何学的にも嬉しくないです．だから $\boldsymbol{r} \colon \mathbb{R}_+ \times S^2 \longrightarrow \mathbb{R}^3$ を考えてみよう，ということになります．

さて，写像 $\boldsymbol{r} \colon \mathbb{R}_+ \times S^2 \longrightarrow \mathbb{R}^3$ は多様体の埋め込み (embedding) と呼ばれる $C^\infty$ 写像¹の一例です．連続写像なので，多様体の各点 $p \in \mathbb{R}_+ \times S^2$ において微分写像 (differential map) と呼ばれる準同型

    \boldsymbol{r}_* \colon T_p\bigl(\mathbb{R}_+ \times S^2\bigr) \longrightarrow T_{\boldsymbol{r}(p)}\mathbb{R}^3,\; 
    v \longmapsto \bigl(\, f \mapsto v( f \circ \boldsymbol{r}) \,\bigr)

を自然に誘導します．

... なんだかややこしくなってきたので微分写像を座標表示してみましょう．$v \in T_p\bigl(\mathbb{R}_+ \times S^2\bigr)$ なので，自然基底で

    v = v^r \frac{\partial}{\partial r} + v^\theta \frac{\partial}{\partial \theta} + v^\phi \frac{\partial}{\partial \phi}

と展開します．$\boldsymbol{r}_* v = w \in T_{\boldsymbol{r}(p)}\mathbb{R}^3$ についても同様に

    w = w^x \frac{\partial}{\partial x} + w^y \frac{\partial}{\partial y} + w^x \frac{\partial}{\partial z}

と展開すると，$\forall f \in C^{\infty}\bigl(\mathbb{R}^3)$ に対して

\begin{align}
    &w^x \frac{\partial(f \circ \psi^{-1})}{\partial x} + w^y \frac{\partial(f \circ \psi^{-1})}{\partial y} + w^x \frac{\partial(f \circ \psi^{-1})}{\partial z} \\
    =\; &v^r \frac{\partial(f \circ \boldsymbol{r} \circ \varphi^{-1})}{\partial r} + v^\theta \frac{\partial(f \circ \boldsymbol{r} \circ \varphi^{-1})}{\partial \theta} + v^\phi \frac{\partial(f \circ \boldsymbol{r} \circ \varphi^{-1})}{\partial \phi}
\end{align}

$f$ は任意だったので，例えば $f = x$ などと選ぶと $f \circ \psi^{-1} = x,\; f \circ \boldsymbol{r} \circ \varphi^{-1} = x(r,\,\theta,\, \phi)$ となり

w^x = 
\begin{bmatrix}
    \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} & \frac{\partial x}{\partial\phi}
\end{bmatrix}
\begin{bmatrix}
    v^r \\
    v^\theta \\
    v^\phi
\end{bmatrix}

で，$f = y,, z$ についても同様に計算すると，自然基底で展開した係数の変換則が

\begin{bmatrix}
    w^x \\
    w^y \\
    w^z
\end{bmatrix}
= 
\begin{bmatrix}
    \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} & \frac{\partial x}{\partial\phi} \\
\frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} & \frac{\partial y}{\partial\phi} \\
\frac{\partial z}{\partial r} & \frac{\partial z}{\partial \theta} & \frac{\partial z}{\partial\phi}
\end{bmatrix}
\begin{bmatrix}
    v^r \\
    v^\theta \\
    v^\phi
\end{bmatrix}

であることがわかります．i.e. 微分写像 $\boldsymbol{r}_* \colon T_p\bigl(\mathbb{R}_+ \times S^2\bigr) \longrightarrow T_{\boldsymbol{r}(p)}\mathbb{R}^3,\;
v \longmapsto \bigl(\, f \mapsto v( f \circ \boldsymbol{r}) \,\bigr)$ はJacobi行列を表現行列とする線型写像なのです．

まとめると，$C^\infty$ 級の連続写像

    \boldsymbol{r} \colon \mathbb{R}_+ \times S^2 \longrightarrow \mathbb{R}^3

から加群の準同型

    \boldsymbol{r}_* \colon T_p \bigl( \mathbb{R}_+ \times S^2 \bigr)
    \longrightarrow T_p(\mathbb{R}^3)

が自然に構成されました²．

余接空間の構成

接空間 $T_p\bigl(\mathbb{R}_+ \times S^2\bigr)$ はベクトル空間なので，その双対ベクトル空間 $T_p^*\bigl(\mathbb{R}_+ \times S^2\bigr)$ を考えることができます．このベクトル空間には余接空間 (cotangent space) という名前がついています．

    T_p^*\bigl(\mathbb{R}_+ \times S^2\bigr) := 
    \bigl\{ \, \omega \colon T_p \bigl(\mathbb{R}_+ \times S^2\bigr) \longrightarrow \mathbb{R} \bigm| 線型写像 \bigr\}

双対ベクトル空間 $T_p^*\bigl(\mathbb{R}_+ \times S^2\bigr)$ の基底として

    \mathrm{d}x^\mu(\partial_\nu) = \delta^\mu_\nu

を充たす3つの線型写像 $\mathrm{d}r,\, \mathrm{d}\theta,\, \mathrm{d}\phi$ を選ぶことができます（双対基底; dual basis）．それらしい記号を使っていますが，ここまではただ余接空間の基底を文字で置いただけです．

$\forall \omega \in T_p^*\bigl(\mathbb{R}_+ \times S^2\bigr)$ は線型写像なので $\forall v = v^\mu \partial_\mu \in T_p \bigl( \mathbb{R}_+ \times S^2 \bigr)$ に作用させると

   \omega(v) = v^\mu \omega(\partial_\mu) 
   = \omega(\partial_\mu)\mathrm{d} x^\nu(v) 
   = \bigl(\omega(\partial_\mu) \mathrm{d}x^\nu \bigr)(v)

かつ $\omega(\partial_\mu) \in \mathbb{R}$ なので $\omega$ が $\mathrm{d}x^\mu$ >で展開されたことになりますし，$a_\mu \mathrm{d}x^\mu = 0$ が成り立つならば

   a_\mu = a_\nu \delta_\mu^\nu
   = a_\nu \mathrm{d} x^\nu (\partial_\mu)
   = \bigl( a_\nu \mathrm{d} x^\nu\bigr)(\partial_\mu) = 0

となるので $\lbrace \mathrm{d} x^\nu \rbrace_{\nu = 1,2,3}$ は線型独立です．

具体的に双対基底 $\mathrm{d}r,\, \mathrm{d}\theta,\, \mathrm{d}\phi$ を構成するには，関数 $f \in C^\infty \bigl( \mathbb{R}_+ \times S^2 \bigr)$ の微分 (differential of $f$) を

    (\mathrm{d}f)_p \colon  T_p \bigl( \mathbb{R}_+ \times S^2 \bigr) \longrightarrow \mathbb{R},\; v \longmapsto v(f)

として定義すると良いです．$(\mathrm{d}f)_p \in T_p^* \bigl( \mathbb{R}_+ \times S^2 \bigr) $ となっていることがポイントです．

座標関数 $x^\mu \in C^\infty \bigl( \mathbb{R}_+ \times S^2 \bigr)$ の微分は

    (\mathrm{d}x^\mu)_p (\partial_\nu)= \frac{\partial x^\mu}{\partial x^\nu} = \delta^\mu_\nu 

となり，$(\mathrm{d}x^\mu)_p$ が余接空間の双対基底になっていることがわかりました．

テンソル場の構成

記号がややこしくなってきたのと，一般の $C^\infty$ 多様体に関して全く同様に議論できるので，以降では今まで $\mathbb{R}_+ \times S^2$ と書いていたところを一般の $d$ 次元 $C^\infty$ 多様体 $M$ に書き換えます．

多様体 $M$ 上の点 $p$ における $(r,\, s)$ 型テンソル空間 $\mathcal{T}^r_s(T_p M)$ を次のように定義できます：

\begin{align}
    \mathcal{T}^r_s(M) &:= \bigl\{ \, \alpha \colon \underbrace{T^*_pM \times \cdots \times T^*_pM}_{r} \times \underbrace{T_pM \times \cdots \times T_pM}_{s} \to \mathbb{R} \\
&\quad \bigm| \alpha\; は各変数について線型な多重線型写像 \, \bigr\}
\end{align}

この背景には加群上のテンソル積の普遍性があるのですが，実用上は上の定義で十分な気がします．

$\mathcal{T}^r_s(T_p M)$ 自身もベクトル空間なので，基底を構成しましょう．そのためには勝手な $r$ 個の接ベクトル $v_i \in T_p M$ と $s$ 個のコベクトル $\omega_i \in T^*_p M$ から $\mathcal{T}^r_s(T_pM)$ の元を作る方法（テンソル積）を次のように構成します：

作りたい $\mathcal{T}^r_s(T_p M)$ の元は勝手な $r$ 個のコベクトル $\alpha_i \in T^*_p M$ と $s$ 個の接ベクトル $w_i \in T_p M$ を引数にもつ写像です．これを記号として

v_1 \otimes \cdots \otimes v_r \otimes \omega_1 \otimes \cdots \otimes \omega_s \in \mathcal{T}^r_s(T_pM)

と書き，

\begin{align}
&\bigl( v_1 \otimes \cdots \otimes v_r \otimes \omega_1 \otimes \cdots \otimes \omega_s \bigr)\bigl(\alpha_1,\, \dots ,\, \alpha_r;\; w_1,\, \dots ,\, w_s \bigr) \\
&:= \prod_{i = 1}^r \prod_{j=1}^s \alpha_i(v_i) \omega_j(w_j)
\end{align}

で定義します．右辺はただの実数になっているのでこれで良いです．

$\mathcal{T}^r_s(T_p M)$ の基底は

    \mathcal{B} = \bigl\{ \partial_{\mu_1} \otimes \cdots \otimes \partial_{\mu_r} \otimes \mathrm{d} x^{\nu_1} \otimes \cdots \otimes \mathrm{d} x^{\nu_s} \bigm| 1 \le \mu_a,\, \nu_b \le d \bigr\}

です．

まず $\forall T_p \in \mathcal{T}_s^r(T_p M)$ が $\mathcal{B}$ の元の線形結合で書けることを示します．全部で $d^{r+s}$ 通りある全ての添字の組み合わせ $(\mu_a,\, \nu_b )$ に対して実数

T^{\mu_1\dots\mu_r}{}_{\nu_1\dots\nu_s} := T_p\bigl(\mathrm{d}x^{\mu_1}, \,\dots,\, \mathrm{d} x^{\mu_r},\, \partial_{\nu_1},\, \dots, \partial_{\nu_s}\bigr)

を定めることができます．示すべきは

T_p = T^{\mu_1\dots\mu_r}{}_{\nu_1\dots\nu_s} \partial_{\mu_1} \otimes \cdots \otimes \partial_{\mu_r} \otimes \dd{x^{\nu_1}} \otimes \cdots \otimes \mathrm{d} x^{\nu_s}

です．実際，勝手な $r$ 個のコベクトル $\alpha_i \in T^*_p M$ と $s$ 個の接ベクトル $w_i \in T_p M$ に対して

\begin{align}
  &T^{\mu_1\dots\mu_r}{}_{\nu_1\dots\nu_s} \partial_{\mu_1} \otimes \cdots \otimes \partial_{\mu_r} \otimes \dd{x^{\nu_1}} \otimes \cdots \otimes \mathrm{d} x^{\nu_s}(\alpha_1,\, \dots,\, \alpha_r;\; w_1,\, \dots ,\, w_s) \\
&= T^{\mu_1\dots\mu_r}{}_{\nu_1\dots\nu_s} \alpha_1(\partial_{\mu_1}) \cdots \alpha_r(\partial_{\mu_r}) \dd{x^{\nu_1}}(w_1) \cdots \dd{x^{\nu_s}}(w_s) \\
&= T^{\mu_1\dots\mu_r}{}_{\nu_1\dots\nu_s} \alpha_1{}_{\mu_1} \cdots \alpha_r{}_{\mu_r} w_1{}^{\nu_1} \cdots w_s{}^{\nu_s}
\end{align}

一方，左辺は多重線型性から

\begin{align}
  &T_p(\alpha_1,\, \dots,\, \alpha_r;\; w_1,\, \dots ,\, w_s) \\
  &= T_p(\alpha_1{}_{\mu_1} \dd{x^{\mu_1}},\, \dots,\, \alpha_r{}_{\mu_r} \dd{x^{\mu_r}};\; w_1{}^{\nu_1} \partial_{\nu_1},\, \dots ,\, w_s{}^{\nu_s}\partial_{\nu_s})\\
  &= T^{\mu_1\dots\mu_r}{}_{\nu_1\dots\nu_s} \alpha_1{}_{\mu_1} \cdots \alpha_r{}_{\mu_r} w_1{}^{\nu_1} \cdots w_s{}^{\nu_s}
\end{align} 

なので示せました．

次に，$\mathcal{B}$ が線型独立であることを示します．先程と同様の記号を使って

T^{\mu_1\dots\mu_r}{}_{\nu_1\dots\nu_s} \partial_{\mu_1} \otimes \cdots \otimes \partial_{\mu_r} \otimes \dd{x^{\nu_1}} \otimes \cdots \otimes \mathrm{d} x^{\nu_s} = 0

を仮定し，左辺の多重線型写像の引数に $\dd{x^{\kappa_a}},\; \partial_{\lambda_b}$ を代入することで，全ての添字の組み合わせに対して

 T^{\kappa_1\dots \kappa_r}{}_{\lambda_1\dots\lambda_s} = 0

とわかります．i.e. $\mathcal{B}$ は線型独立です．

多様体の各点 $p \in M$ において テンソル空間 $\mathcal{T}^r_s(T_p M)$ を構成できました．これらを多様体 $M$ 全域にわたって「なめらかに繋ぎ合わせる」とテンソル場 (tensor field) $\mathfrak{T}^r_s(M)$ の完成です．「なめらかに繋ぎ合わせる」と言うのは，

T_p = T^{\mu_1\dots\mu_r}{}_{\nu_1\dots\nu_s}(p) \partial_{\mu_1} \otimes \cdots \otimes \partial_{\mu_r} \otimes \dd{x^{\nu_1}} \otimes \cdots \otimes \mathrm{d} x^{\nu_s} \in \mathcal{T}^r_s(T_pM)

の $p$ を動かした時に展開係数から自然に定まる $d^{r+s}$ 個の関数

T^{\mu_1\dots\mu_r}{}_{\nu_1\dots\nu_s} \colon M \longrightarrow \mathbb{R},\; p \longmapsto  T^{\mu_1\dots\mu_r}{}_{\nu_1\dots\nu_s}(p) 

が $C^\infty$ 級になると言うことです．

「なめらかに繋ぎ合わせる」操作は，ベクトル束 (vector bundle)

T^r_s TM := \coprod_{p \in M} T^r_s(T_pM)

の切断 (section) をとることに相当します．記号としては

    \mathfrak{T}^r_s(M) = \Gamma \bigl( T^r_s TM \bigr) 

とか書くことが多いと思います．$\Gamma \bigl( T^r_s TM \bigr)$ は無限次元 $\mathbb{R}$ ベクトル空間であると同時に左 $C^\infty(M)$ 加群でもあります．

Riemann計量を求める

ここで，Riemann計量 (Riemannian metric) $g$ を $(0,\, 2)$ 型テンソル場であって
各点 $p \in M$ において

    g_p \colon T_p M \times T_p M \longrightarrow \mathbb{R}

が正定値内積の公理を充たすものと定義します：

1. $g_p$ は双線型写像である．
2. $\forall u,, v \in T_p^*M,\; g_p(u,\, v) = g_p(v,\, u)$
3. $\forall u \in T_p^*M,\; g_p(u,\, u) \ge 0$ かつ等号成立は $u = 0$ のときのみ

成分表示すると

g = g_{\mu\nu} \dd{x^\mu} \otimes \dd{x^\nu}

になります．
内積の公理 2 から，$d \times d$ 個の $C^\infty$ 関数を成分に持つ行列 $\bigl[g_{\mu\nu} \bigr]_{1 \le \mu,, \nu \le d}$ は対称行列になります：

 g_{\mu\nu} = g_{\nu\mu}

一般相対論で登場する計量との関係は，微小変位を表すベクトル場 $\dd{s} = \dd{y^\mu} \partial_\mu \in \mathfrak{X}(M)$ （この $\dd{y^\mu}$ は無限小変位を表すもので，コベクトルではないです．また，無限小変位と言っても多様体上の点を動かすものではないことに注意です）のノルムの二乗

\begin{align}
    \dd{s}^2 &= g(\dd{y^\mu} \partial_\mu,\; \dd{y^\nu} \partial_\nu) \\
    &= g_{\kappa\lambda} \dd{y^\mu} \dd{y^\nu} (\dd{x^\kappa} \otimes \dd{x^\lambda})(\partial_\mu,\, \partial_\nu) \\
    &= g_{\kappa\lambda} \dd{y^\mu} \dd{y^\nu} \dd{x^\kappa}(\partial_\mu) \dd{x^\lambda}(\partial_\nu) \\
    &= g_{\mu\nu} \dd{y^\mu}\dd{y^\nu}
\end{align}

で明かでしょう．

さて，いま2つのRiemann多様体 $(M,\, g),\; (N,\, h)$ があって，うち $h = h_{\mu\nu} \dd{y^\mu} \otimes \dd{y^{\nu}}$ の成分 $[h_{\mu\nu}]$ が分かっている状況を考えます．
この状態で $C^\infty$ 級のはめ込み (immersion)

f \colon M \to N

が与えられたら，$g = g_{\mu\nu} \dd{x^\mu} \otimes \dd{x^\nu}$ の具体形を計算できることを確認します．
まず $p \in M$ を一つ固定し，$p \in U \subset M$ なる $M$ のチャート $(U;\, x^1,\, \dots ,\, x^m)$ および $f(p) \in V \subset N$ なる $N$ のチャート $(V;\, y^1,\, \dots ,\, y^n)$ をとります．$M$ と $N$ の次元が違っても良いです．

h_{f(p)} \colon T_{f(p)} N \times  T_{f(p)} N \longrightarrow \mathbb{R}

は与えられているので，これを元に

g_p \colon T_pM \times T_pM \longrightarrow \mathbb{R}

を構成するには $T_p M$ と $T_{f(p)} N$ を繋ぐ都合の良い連続写像が欲しいです．幸にして，先程定義した $f$ の微分写像はちょうどこの要件を充していますね．つまり，

g_p \colon T_pM \times T_pM \longrightarrow \mathbb{R},\; (u,\, v) \longmapsto h_{f(p)} \bigl( f_*(u),\, f_*(v) \bigr) 

とすれば良いでしょう．$f \colon M \to N$ が $C^\infty$ 級のはめ込みなので，このようにして構成した $g$ は正定値内積の公理を充します．

誘導計量 $g = f_* h$ は，テンソル場の引き戻し (pullback) と呼ばれるものの一例です．多様体上のテンソル場の引き戻しは位相空間の圏から加群の圏への反変関手です．

$g_p$ を成分表示してみます：

\begin{align}
    &g_{\mu\nu}(p) = g_p(\partial_\mu,\, \partial_\nu) \\
    &= h_{f(p)} \left( f_*\biggl(\pdv{}{x^\mu}\biggr),\, f_*\biggl(\pdv{}{x^\nu}\biggr) \right) \\
    &= h_{f(p)} \left( \pdv{y^{\kappa}}{x^{\mu}} \pdv{}{y^\kappa},\, \pdv{y^{\lambda}}{x^{\nu}} \pdv{}{y^\lambda} \right) \\
    &= h_{\kappa\lambda} \bigl( f(p) \bigr)  \pdv{y^{\kappa}}{x^{\mu}} \bigl( f(p) \bigr) \pdv{y^{\lambda}}{x^{\nu}} \bigl( f(p) \bigr)
\end{align} 

とくにEuclid空間 $(\mathbb{R}^d,\, \delta)$ へのはめ込み $\boldsymbol{r} \colon M \longrightarrow \mathbb{R}^d$ が与えられた場合，計算は劇的に簡単になります．Euclid空間の計量の成分は $\delta_{\mu\nu}$ であり，$\pdv{y^{\nu}}{x^{\mu}} \bigl( f(p) \bigr)$ は単に $\pdv{\boldsymbol{r}}{x^\mu}$ の第 $\nu$ 成分なので，単に

    g_{\mu\nu} = \pdv{\boldsymbol{r}}{x^\mu} \cdot \pdv{\boldsymbol{r}}{x^\nu}

を計算すれば良いからです（この $\cdot$ はEuclid内積です）．一般相対論の教科書でたまに計量テンソルの定義として見かける式ですね．

3次元極座標の計量

冒頭で用意した，3次元極座標 $(r,\, \theta,\, \phi)$ の計量を誘導計量の方法を用いて計算して見ましょう．はめ込みは

    \boldsymbol{r}(r,\, \theta,\, \phi) 
= \begin{bmatrix}
    x(r,\, \theta,\, \phi) \\
    y(r,\, \theta,\, \phi) \\
    z(r,\, \theta,\, \phi)
\end{bmatrix} 
=
\begin{bmatrix}
    r \sin \theta \cos \phi \\
    r \sin \theta \sin \phi \\
    r \cos \theta
\end{bmatrix} 

だったので，

\pdv{\boldsymbol{r}}{r} = 
\begin{bmatrix}
    \sin \theta \cos \phi \\
    \sin \theta \sin \phi \\
    \cos \theta
\end{bmatrix}, \quad
\pdv{\boldsymbol{r}}{\theta} = 
\begin{bmatrix}
    r\cos \theta \cos \phi \\
    r\cos \theta \sin \phi \\
    -r\sin \theta
\end{bmatrix}, \quad
\pdv{\boldsymbol{r}}{\phi} = 
\begin{bmatrix}
    -r \sin \phi \\
    r \cos \phi \\
    0
\end{bmatrix}

です．故に

\begin{align}
    g_{11} &= \pdv{\boldsymbol{r}}{r} \cdot \pdv{\boldsymbol{r}}{r} = 1, \\
    g_{22} &= \pdv{\boldsymbol{r}}{\theta} \cdot \pdv{\boldsymbol{r}}{\theta} = r^2, \\
    g_{33} &= \pdv{\boldsymbol{r}}{\phi} \cdot \pdv{\boldsymbol{r}}{\phi} = r^2 \sin^2 \theta, \\
    g_{\mu\nu} &= 0\quad (\mu \neq \nu)
\end{align} 

と求まりました．なお，関数の微分を用いて

\begin{align}
    \boldsymbol{r}_* h &= (\dd{x(r,\, \theta,\, \phi)})^2 + (\dd{y(r,\, \theta,\, \phi)})^2 + (\dd{z(r,\, \theta,\, \phi)})^2 \\
    &= (\sin \theta \cos \phi \dd{r} + r \cos \theta \cos \phi \dd{\theta} - r \sin \theta \sin \phi \dd{\phi})^2 \\
    &\quad + (\sin \theta \sin \phi \dd{r} + r \cos \theta \sin \phi \dd{\theta} + r \sin \theta \cos \phi \dd{\phi})^2 \\
    &\quad + (\cos \theta \dd{r} - r \sin \theta \dd{\theta} )^2 \\
    &= (\dd{r})^2 + r^2 (\dd{\theta})^2 + r^2 \sin^2 \theta (\dd{\phi})^2
\end{align}

と計算することもできます．どちらを用いるかはお好みでどうぞ．

一般の直交曲線座標の場合

多様体 $M$（$\mathrm{dim} M \le d$）の $d$ 次元Euclid空間への $C^\infty$ 級のはめ込み

\boldsymbol{r} \colon M \longrightarrow \mathbb{R}^d,\; (x^1,\, \dots ,\, x^{\mathrm{dim} M}) \longmapsto \boldsymbol{r}(x^1,\, \dots ,\, x^{\mathrm{dim} M})

が与えられたとしましょう．もし

\pdv{\boldsymbol{r}}{x^\mu} \cdot \pdv{\boldsymbol{r}}{x^\nu} = h_{(\mu)}^2 \delta_{\mu\nu}

と直交していることがわかった場合，計量の成分表示は

    [g_{\mu\nu}] = \mathrm{diag} \bigl( h_{(1)}^2,\, h_{(2)}^2 ,\, \dots ,\, h_{(\mathrm{dim}M)}^2 \bigr) 

になることがわかります．$h_{(\mu)}$ はスケール因子 (scale factor) と呼ばれ，Euclidノルムの意味で

    h_{(\mu)} = \lvert\pdv{\boldsymbol{r}}{x^\mu}\rvert

とすれば計算できます．先程の3次元極座標の場合

    h_{(1)} = 1,\; h_{(2)} = r,\; h_{(3)} = r\sin\theta

でした．他にも円筒座標 $(\rho,\, \phi,\, z)$ なら

    h_{(1)} = 1,\; h_{(2)} = \rho,\; h_{(3)} = 1

です．

球面の計量

順番が逆な気もしますが，多様体の次元が違う場合の例として球面の計量も計算しておきましょう．
はめ込みは

\boldsymbol{r}(\theta,\, \phi) = 
\begin{bmatrix}
    \sin \theta \cos \phi \\
    \sin \theta \sin \phi \\
    \cos \theta
\end{bmatrix} 

ですから

\pdv{\boldsymbol{r}}{\theta} =
\begin{bmatrix}
    \cos\theta  \cos \phi \\
    \cos\theta  \sin \phi \\
    -\sin\theta 
\end{bmatrix} ,\quad
\pdv{\boldsymbol{r}}{\phi} =
\begin{bmatrix}
    \sin\theta \sin \phi \\
    -\sin\theta \cos \phi \\
    0
\end{bmatrix} 

であり，即座に

g = \dd{\theta} \otimes \dd{\theta} + \sin^2 \theta \dd{\phi} \otimes \dd{\phi}

と求まります．

添字の上げ下げ

Riemann計量が与えられて嬉しいことは，無限次元ベクトル空間である接バンドル $\boldsymbol{TM}$ と余接バンドル $\boldsymbol{T^*M}$ がベクトル空間として同型になることです．実際，多様体の各点 $p \in M$ において

\hat{g}_p \colon T_pM \longrightarrow T_p^*M,\; v \longmapsto \bigl( \, u \mapsto g_p(v,\, u) \, \bigr) 

として接空間 $T_pM$ から余接空間 $T_p^*(M)$ への準同型を構成すると，これは全単射なので同型になっています．

$\hat{g}_p$ が線型写像であることは明らかです．全単射であることは，Riemann計量が充たす正定値内積の公理3（正定値性）から従います．
実際， $\forall v_1,\, v_2 \in T_pM$ に対して

\begin{align}
   v_1 - v_2 \neq 0 \quad &\Longrightarrow \quad (\hat{g}_p(v_1) - \hat{g}_p(v_2))(v_1 - v_2) = g_p(v_1 - v_2,\, v_1- v_2) > 0 \\
   &\Longrightarrow \quad \hat{g}_p(v_1) - \hat{g}_p(v_2) \neq 0
\end{align}

なので単射です．全射であることは有限次元の多様体を考えているので $\mathrm{dim} T_pM = \mathrm{dim} T^*_pM$ となり，証明が完了しました．

$\hat{g}_p$ を成分表示してみます．$u = \hat{g}_p(v),\, u = u_\mu \dd{x^\mu},\, v = v^\nu \partial_\nu$ とおくと

u_\mu = g_{\mu\nu} v^\nu

です．i.e. $\hat{g}_p$ は計量 $[g_{\mu\nu}]$ を表現行列とする線型写像なのです．特に添字を一つ下げる働きをすることから，

\flat \colon T_pM \longrightarrow T^*_pM

と書くことがあります（音楽同型; musical isomorphism³）．逆写像は

\sharp \colon T^*_pM \longrightarrow T_pM

で，計量 $[g_{\mu\nu}]$ の逆行列 $[g^{\mu\nu}]$ （共役計量とか言います）を表現行列とする線型写像です．

微分形式

いよいよ主人公となる微分形式 (differential form) を定義します．微分形式は座標に依存しない形で定義できるので，添字の苦しみを味わうことなく多様体上で微積分できるようになります（この記事ではそこまで行けませんが...）．物理との対応で言うと，共変性の概念との相性も良いです．

外積代数

まず，$n < \infty$ 次元多様体 $M$ 上の一点 $p \in M$ を固定して，$p$ を含むチャート $(U;,\, x^1,\, \dots,\, x^n)$ をとります．そして，余接空間 $T^*_p M$ を素材にして次のような性質を持った，外積代数 (exterio algebra) と呼ばれる多元環 $\left( \bigwedge^\bullet (T_pM),\, +,\, \wedge \right)$ を構成します：

1. $\mathbb{R}$ 上 $T^*_p M$ の元によって生成される．
2. 単位元 $1$ を持つ
3. 任意の $x,\, y \in V$ に対して以下の関係式が成り立つ：

\begin{align}
    x \wedge y = - y \wedge x
\end{align}

$\forall x \in T^*_p M$の次数を $1$ とおくことで，$\bigwedge^\bullet (T_p^*M)$ の単項式の次数が定義されます．次数が $k$ の単項式の $\mathbb{R}$ 係数線型結合全体の集合を $\bigwedge^k (T_p M)$ と書くと，ベクトル空間の直和として

\begin{align}
	\bigwedge^\bullet (T_p^*M) = \bigoplus_{k=0}^\infty \bigwedge^k (T_p^*)
\end{align}

と書けます．なお，$\bigwedge^0(T_p^*M) = \mathbb{R}$ と約束します．定義からすぐわかることは，

\bigwedge^1(T_p^*M) \cong T_p^*M

となることです．この意味で余接空間 $T_p^*M$ の元のことをコベクトル以外に1-形式 (1-form) と呼びます．

$\bigwedge^k (T_p^*M)$ はベクトル空間なので，基底を構成します．
$\dd{x^{\mu_1}} \wedge \cdots \wedge \dd{x^{\mu_k}}$ の形をした単項式のうち，互いに線形独立なものである．定義の性質3より，添字の組 $(\mu_1,\, \dots ,\, \mu_k)$ の中に互いに等しいものがあると $0$ になり，かつ，添字の順番を並べ替えただけの項は線形独立になりません．以上の考察から，
$\bigwedge^k (T_p^*M)$ の基底として

\begin{align}
		\mathcal{E} := \bigl\{\, \dd{x^{\mu_1}} \wedge \cdots \wedge \dd{x^{\mu_k}} \bigm| 1 \le \mu_1 < \cdots < \mu_k \le n \, \bigr\}
\end{align}

をとることができます．このとき $\mathcal{E}$ の要素数を数えることで

\dim \bigwedge^k (T_p^*M) =
\begin{pmatrix}
 n \\
 k
\end{pmatrix}

とわかります．
さらに二項定理から，$\dim \bigwedge^\bullet (T_p^*M) = 2^n$ です．また，$k > n$ のとき $\bigwedge^k (T_p^*M) = { 0 }$ です．

交代形式

$k$-形式を定義したはいいものの，上述の定義はいささか抽象的でいまいち多様体と結びつきません．しかし，実は $\bigwedge^k(T_p^*M)$ は $(0,\, k)$ 型テンソル空間の部分空間のうち，
交代形式 (alternating form) と呼ばれるものになっています．

$r$ 次の交代形式とは，$(0,\, r)$ 型テンソル $ \omega \in \mathcal{T}_r^0 (T_p M)$ であって，任意の置換
$\sigma \in \mathfrak{S}_r$ に対して

\begin{align}
		\omega \bigl[ X_{ \sigma(1) },\, \dots ,\, X_{ \sigma(r) } \bigr] = \mathrm{sgn}\, \sigma\; \omega \bigl[ X_1,\, \dots ,\, X_r \bigr],\quad X_i \in T_pM
\end{align}

となるもののことです．

$r$ 次の交代形式全体の集合を $A^r(T_p M)$ と書いて，字数の異なる交代形式を全て集めてできるベクトル空間

\begin{align}
	A^\bullet (T_pM) := \bigoplus_{r = 0}^\infty A^r(T_pM)
\end{align}

を考えます．ただし $A^0(T_p M) = \mathbb{R}$ と定義します．交代性より $k > n$ のとき $A^k(T_p M) = { 0 }$ になります．
ここで，ベクトル空間の同型

\bigwedge^\bullet(T_p^*M) \cong A^\bullet (T_pM)

を与える同型写像を具体的に構成してみましょう．

写像 $ \iota \colon \bigwedge^\bullet (T_p^*M) \to A^\bullet(T_p M)$ を以下のように定義する：

まず，写像 $ \iota_k \colon \bigwedge^k (T_p^*M) \to A^k(T_pM)$ の $ \omega = \alpha_1 \wedge \cdots \wedge \alpha_k\in \bigwedge^k (T_p^*M) \; ( \alpha_i \in T_p^*M )$ への作用を

\begin{align}
  	\iota_k( \omega )[X_1,\, \dots ,\, X_k] := \det \bigl(\, \alpha_i [X_j] \, \bigr)
  \end{align}

と定義する．$\forall \omega \in \bigwedge^\bullet (T_p M)^*$ に対する $ \iota $ の作用は $ \iota_k $ の作用を線形に拡張する．

このとき，$ \iota $ が求めるべき同型写像である．

各 $ \iota_k $ が同型写像であることを示せば良いですが，$\bigwedge^k (T_p^*M)$ の基底を

 \begin{align} 
 	\bigl\{\, e^{i_1} \wedge \cdots \wedge e^{i_k} \bigm| 1 \le i_1 < \cdots < i_k \le n \,\bigr\}
 \end{align}

ととれるので，

\bigl\{\, \iota_k \bigl( \dd{x^{i_1}} \wedge \cdots \wedge \dd{x^{i_k}} \bigr) \bigm| 1 \le i_1 < \cdots < i_k \le n \,\bigr\} \subset A^k(T_pM)

が $A^k(T_pM)$ の基底を成すことを示せばよいです．
以下では入力がめんどくさいので $\dd{x^{i_l}}$ を $e^{i_l}$ と略記します（実はこの節の議論は純粋に代数的で， $T_pM$ に限らず一般のベクトル空間 $V$ に対して成り立ちます）．

ある $\lambda_{i_1 \dots i_k} \in \mathbb{R}$ に対して

\begin{align} 
	\sum_{1 \le i_1 < \cdots < i_k \le n}\lambda_{i_1 \dots i_k} \iota_k \bigl( e^{i_1} \wedge \cdots \wedge e^{i_k}\bigr) = 0 \in A^k(T_pM)
\end{align}

ならば，

\begin{align} 
	0 &= \sum_{1 \le i_1 < \cdots < i_k \le n} \lambda_{i_1 \dots i_k} \iota_k \bigl( e^{i_1} \wedge \cdots \wedge e^{i_k} \bigr) [e_{j_1}, \dots ,\, e_{j_k}] \\
	&= \sum_{1 \le i_1 < \cdots < i_k \le n} \lambda_{i_1 \dots i_k} \det \bigl( e^{i_l}[e_{j_m}] \bigr) \\
	&= \sum_{1 \le i_1 < \cdots < i_k \le n} \lambda_{i_1 \dots i_k} \det \bigl( \delta^{i_l}_{j_m} \bigr) \\
	&= \lambda_{j_1 \dots j_k} 
\end{align}

なので線形独立です．

次に $\forall \omega \in A^k(T_p M)$ を一つとります．このとき $\omega_{i_1 \dots i_k} := \omega[e_{i_1},\, \dots ,\, e_{i_k}]$ とおいて

\begin{align} 
	\tilde{\omega} := \sum_{1 \le i_1 < \cdots < i_k \le n} \omega_{i_1 \dots i_k} e^{i_1} \wedge \cdots \wedge e^{i_k} \in \bigwedge^k(T_p^*M)
\end{align}

と定義すると

\begin{align} 
	\iota_k(\tilde{\omega}) = \sum_{1 \le i_1 < \cdots < i_k \le n} \omega_{i_1 \dots i_k} \iota_k \bigl( e^{i_1}\wedge \cdots \wedge e^{i_k} \bigr) = \omega
\end{align}

なので $\iota_k$ は全射です．従って $\iota_k \colon \bigwedge^\bullet(T_p^*M) \xrightarrow{\cong} A^k(T_pM)$ です．

上の方法で構成した $\iota_k$ は定数倍しても同型写像を与えます．文献によっては $1/k!$ 倍されていたりするので注意です．

外積代数と交代形式は同型なので，外代数が元々持っていた積演算 $\wedge$ は交代形式においても保存されたままです．つまり，交代形式上にも外積 $\wedge$ が定まります．

$\tilde{\omega} \in \bigwedge^k(T_p^*M),\; \tilde{\eta} \in \bigwedge^l(T_p^*M)$ を与えます．先程定義した同型写像 $\iota \colon \bigwedge^\bullet(T_p^*M) \xrightarrow{\cong} A^\bullet(T_pM)$ による対応を

\begin{align} 
		\tilde{\omega} &\longmapsto \omega := \iota(\tilde{\omega}), \\
		\tilde{\eta} &\longmapsto \omega := \iota(\tilde{\eta}), \\
		\tilde{\omega}\wedge \tilde{\eta} &\longmapsto \omega \wedge \eta := \iota(\tilde{\omega} \wedge \tilde{\eta})
	\end{align}

とおくと， $A^\bullet(T_pM)$ 上の外積 (exterior product) $\wedge \colon A^k(T_p M) \times A^l(T_p M) \to A^{k+l}(T_p M)$ が次のようにして定まります：

\begin{align} 
		&(\omega \wedge \eta)[X_1,\, \dots ,\, X_{k+l}] \\
		&= \frac{1}{k !\, l !} \sum_{\sigma \in \mathfrak{S}_{k+l}} \sgn{\sigma} \omega[X_{\sigma(1)},\, \dots ,\, X_{\sigma(k)}]\, \eta[X_{\sigma(k+1)},\dots ,\, X_{\sigma(k+l)}]
\end{align}

多様体上の微分形式

ややこしかった前節の結果を用いて，局所座標表示に依存しない微分形式の定義を与えることができます：

$M$ を $C^\infty$ 多様体とする．$\omega$ が $M$ 上の $\boldsymbol{k}$-形式 ($k$-form) であるとは，各点 $p \in M$ において $\omega_p \in \bigwedge^k\bigl(T^*_pM\bigr)$ を対応させ，$\omega_p$ が $p$ に関して $C^\infty$ 級であることを言う．

ベクトル束の言葉を使うと，これもまた切断

\begin{align} 
	\Omega^k(M) = \Gamma\left(\coprod_{p \in M} \bigwedge^k\bigl(T^*_pM\bigr)\right)
\end{align}

です．

$(0,\, r)$-階テンソル場としての側面を明らかにしてくれる命題は次のようなものです：

$M$ を $C^\infty$ 多様体とする．$M$ 上の $k$-形式全体の集合 $\Omega^k(M)$ は，

\begin{align} 
  	\bigl\{\, &\tilde{\omega} \colon \mathfrak{X}(M) \times \cdots \times \mathfrak{X}(M) \to C^\infty(M) \\
  	\bigm| \; &\tilde{\omega}\; \text{は}\;C^\infty(M)\;\text{-加群として多重線型かつ交代的}\; \bigr\} 
  \end{align}

と自然に同型である．

つまり，$k$ 個のベクトル場 $X_i \in \mathfrak{X}(M)$ を引数にもち $C^\infty$ 関数を返す何らかの写像 $\mathcal{M}$ を作ったとき，$\mathcal{M}$ が $C^\infty(M)$ 加群の意味で多重線型写像で，かつ引数の入れ替えに関して交代的ならば，$\mathcal{M}$ のことを $k$-形式と同一視できます．

微分形式の演算

外積

$k$-形式と $l$-形式の外積

\begin{align} 
	\wedge \colon \Omega^k(M) \to \Omega^l(M),\; (\omega,\, \eta) \mapsto \omega \wedge \eta
\end{align}

は，各点 $p \in M$ で

\begin{align} 
	(\omega \wedge \eta)_p := \omega_p \wedge \eta_p \in A^{k+l}(T_p M)
\end{align}

と定義される双線型写像です．

外積の基本的な性質は

1. $\eta \wedge \omega = (-1)^{kl} \omega \wedge \eta$
2. 任意のベクトル場 $X_1,, \dots ,, X_{k+l} \in \mathfrak{X}(M)$ に対して

\begin{align} 
	&(\omega \wedge \eta)(X_1,\, \dots ,\, X_{k+l}) \\
	&= \frac{1}{k !\, l !} \sum_{\sigma \in \mathfrak{S}_{k+l}} \sgn{\sigma} \omega(X_{\sigma(1)},\, \dots ,\, X_{\sigma(k)})\, \eta(X_{\sigma(k+1)},\dots ,\, X_{\sigma(k+l)})
\end{align}

です．

外微分

超重要です．まず座標表示に依存する形で定義します．

$M$ のチャート $(U;\, x^i)$ を与えます．$k$-形式 $\omega \in \Omega^k(M)$ の座標表示が

\begin{align} 
	\omega = \omega_{i_1 \cdots i_k} \dd{x^{i_1}} \wedge \cdots \wedge \dd{x^{i_k}} 
\end{align}

と与えられたとき，外微分 (exterior differention)

\begin{align} 
		\dd{} \colon \Omega^k(M) \to \Omega^{k+1}(M)
\end{align}

は次のように定義さます：

\begin{align} 
		\dd{\omega} := \pdv{\omega_{i_1 \cdots i_k}}{x^{j}} \dd{x^{j}} \wedge \dd{x^{i_1}} \wedge \cdots \wedge \dd{x^{i_k}} 
\end{align}

実は，$k$-形式 $\omega \in \Omega^k(M)$ の外微分は任意のベクトル場 $X_1,\, \dots ,\, X_{k+1} \in \mathfrak{X} (M)$ に対して

	\begin{align} 
		\dd{\omega} (X_1,\, \dots ,\, X_{k+1}) = &\sum_{i=1}^{k+1} (-1)^{i+1} X_i \bigl( \omega(X_1,\, \dots ,\, \hat{X_i},\, \dots,\, X_{k+1}) \bigr) \\
		&+ \sum_{i < j} (-1)^{i+j} \omega \bigl( [X_i,\, X_j],\, X_1,\, \dots ,\, \hat{X_i},\, \dots ,\, \hat{X_j},\, \dots ,\, X_{k+1} \bigr) 
	\end{align}

と書けます．ただし $\hat{X_i}$ は $X_i$ を省くことを意味します.

また，$[X,\,Y]$ はLie括弧積と呼ばれる $\mathfrak{X}(M)$ 上の二項演算で，以下のように定義されます：

\begin{align} 
 [X,\,Y]f := X(Yf) - Y(Xf)
\end{align}

この表式は座標に依存しない，理論的においしい表示です（ただ，この表示を使って計算をするのは難しいと思います）．

外微分の基本性質は

\dd{} \circ \dd{} = 0

1. $\omega \in \Omega^k(M)$ のとき

\dd{(\omega \wedge \eta)} = \dd{\omega} \wedge \eta + (-1)^k \omega \wedge \dd{\eta}

です．性質 2 は通常の微分のLeibniz則と $(-1)^k$ の因子だけずれています．このことを指して「外微分は反微分である」などと言うことことがあります．また，性質 1 は $C^\infty(M)$ 加群 $\Omega^q(M)$ と加群の準同型 $\dd{} \colon \Omega^q(M) \to \Omega^{q+1}(M)$ の組の系列

    \cdots \xrightarrow{\dd{}} \Omega^{q-1}(M) \xrightarrow{\dd{}} \Omega^{q}(M) \xrightarrow{\dd{}} \Omega^{q+1}(M) \xrightarrow{\dd{}} \cdots

がコチェイン複体 (cochain complex) を成すことを意味します．このコチェイン複体はde Rham複体 (de Rham complex) と呼ばれ代数トポロジーで登場しますが，ここでは深入りしません．

引き戻し

誘導計量のところでチラッと言いました．二つの $C^\infty$ 多様体 $M,\, N$ の間に $C^\infty$ 写像

f \colon M \longrightarrow N

があるとき，微分写像は

f_* \colon T_pM \longrightarrow T_{f(p)}N,\; v \longmapsto \bigl( \, g \mapsto v(g \circ f)\, \bigr)

と言う準同型として定義されました．これを $C^\infty$ 級に繋ぐことでベクトル場同士の間の準同型

f_* \colon \mathfrak{X}(M) \longrightarrow \mathfrak{X}(N),\; X \longmapsto \Bigl( \, q \mapsto \bigl(\, g \mapsto X_{f^{-1}(q)}(g \circ f) \bigr)\, \Bigr)

が得られます（ベクトル場 $X \in \mathfrak{X}(N)$ は $N$ 上の点 $q$ を引数に持ち，接ベクトル $X_q \in T_q N$ を返す写像なので，真面目に全部書くとこんなにややこしくなってしまいます）．
共変関手です．

$f_*$ の向きを逆にしたような外積代数同士の対応（準同型です）

f^* \colon \bigwedge^k \bigl(T_{f(p)} N\bigr) \longrightarrow \bigwedge^k \bigl(T_{p} M\bigr),\; \omega \longmapsto \bigl( \, (X_1,\, \dots,\, X_k) \mapsto \omega(f_*X_1,\, \dots ,\, f_*X_k) \bigr) 

が定義できて，これを $\forall p \in M$ について $C^\infty$ 級に繋ぐことで

f^* \colon \Omega^k(N) \longrightarrow \Omega^k(M),\; \omega \longmapsto \bigl( \, (X_1,\, \dots,\, X_k) \mapsto \omega(f_*X_1,\, \dots ,\, f_*X_k) \bigr) 

なる $k$ 形式同士の準同型を作ることができます．これを微分形式の引き戻し (pullback) と言います．反変関手です．

引き戻しの基本性質は

1. $\forall \omega \in \Omega^k(N),\; \forall \eta \in \Omega^l(N)$ に対して

f^*(\omega \wedge \eta) = f^* \omega \wedge f^* \eta

1. $\forall \omega \in \Omega^k(N)$ に対して

\dd{(f^*\omega)} = f^*(\dd{\omega})

です．

微分形式の内積について

本日のメインターゲットであるHodge双対を定義する準備として，$k$-形式の内積を定義しなくてはなりません．いつもの流れと同様，今回もまずは $p \in M$ を一つ固定してその上で定義をし，最後に $p$ を動かして $C^\infty$ 級に繋ぐ，と言う方法でいきます⁴．

まずは1-形式です．

\bigwedge^1(T_p^*M) \cong T_p^*M

を思い出すと，Riemann計量 $\boldsymbol{g}$ の共役計量⁵ $G_p \colon T_p^*M \times T_p^*M \to \mathbb{R}$ のことを1-形式の内積だと見做せます ．

これを記号として

\langle \;,\, \rangle \colon \bigwedge^1(T_p^*M) \times \bigwedge^1(T_p^*M) \longrightarrow \mathbb{R},\; (\omega,\, \eta) \longmapsto G_p(\omega,\, \eta)

と書くことにします．

次は $k$-形式に関して

\langle \;,\,\rangle_k \colon \bigwedge^k(T_p^*M) \times \bigwedge^k(T_p^*M) \longrightarrow \mathbb{R}

を定義しますが，$\bigwedge^k(T_p^*M)$ は $\mathbb{R}$ ベクトル空間なので

\alpha_1 \wedge \cdots \wedge \alpha_k

のような形をした元に対して定義するだけで十分です：

\langle \alpha_1 \wedge \cdots \wedge \alpha_k,\, \beta_1 \wedge \cdots \wedge \beta_k\rangle_k :=
\begin{vmatrix}
    \langle \alpha_1,\, \beta_1 \rangle & \langle \alpha_1,\, \beta_2 \rangle & \cdots &  \langle \alpha_1,\, \beta_k \rangle \\
    \langle \alpha_2,\, \beta_1 \rangle & \langle \alpha_2,\, \beta_2 \rangle & \cdots &  \langle \alpha_2,\, \beta_k \rangle \\
    \vdots & \vdots & \ddots & \vdots \\
    \langle \alpha_k,\, \beta_1 \rangle & \langle \alpha_k,\, \beta_2 \rangle & \cdots &  \langle \alpha_k,\, \beta_k \rangle \\
\end{vmatrix}

ただし，定義の右辺は $k\times k$ 行列の行列式をとることを意味します．あとはこれを $\mathbb{R}$ 線型に拡張するだけです．

多脚場

$\Omega^k(M)$ 上に内積が定義されたので，正規直交基底を作れるようになりました．実際に正規直交基底を構成するには多脚場を用いるのが便利です．

多様体の各点 $p \in M$ において行列 $g_{\mu\nu}$ は実対称行列なので，直交行列を用いて対角化できます．そこからさらにスケール変換を施すことで，Riemann計量は⁶

    g_{\mu\nu} = \mathring{g}_{ab} e^a{}_{\mu} e^b{}_{\nu} \quad \mathring{g}_{ab} = \delta_{ab}

と書けます．この $e^a{}_{\mu}$ のことを多脚場 (verbain) と呼びます．
この分解は双対基底 ${, (\dd{x^\mu})_p , }$ の取り替えに対応していて，具体的には

\begin{align} 
	g_p = g_{\mu\nu} (\dd{x^\mu})_p \otimes (\dd{x^\nu})_p = \mathring{g}_{ab} \bigl( \vbud{e}{a}{\mu} (\dd{x^\mu})_p \bigr) \otimes \bigl( \vbud{e}{b}{\nu} (\dd{x^\nu})_p \bigr)
\end{align}

です．こうして得られた $T^*_pM$ の新しい基底を $\{\, \hat{\theta}^a \, \}$ と書きましょう．

$\{\, \hat{\theta}^a\, \}$ に双対的な $T_pM$ の基底 $\{\, \hat{e}_b\, \}$ を $\hat{\theta}^a \bigl[ \hat{e}_b \bigr] = \delta^a_b$ を充たす接ベクトルとして定義します．自然基底からの基底の取り替えを

\hat{e}_a = E_a{}^\nu \left( \pdv{}{x^\nu} \right)_p

とおくと

\begin{align} 
	\delta^a_b &= \hat{\theta}^a \bigl[ \hat{e}_b \bigr] \\
    &= \vbud{e}{a}{\mu} (\dd{x^\mu})_p \left[ \vbdu{E}{b}{\nu} \left( \pdv{}{x^\nu} \right)_p \right]\\
    &= \vbud{e}{a}{\mu} \vbdu{E}{b}{\nu} (\dd{x^{\mu}})_p \left[ \left( \pdv{}{x^\nu} \right)_p  \right] \\
    &= \vbud{e}{a}{\mu} \vbdu{E}{b}{\nu} \delta^\mu_\nu \\
    &= \vbud{e}{a}{\mu} \vbdu{E}{b}{\mu}
\end{align}

が成り立ち， $[\, \vbud{e}{a}{\mu}\, ]$ と $[\, \vbdu{E}{b}{\nu}\, ]$ は互いに逆行列です．
この事実と $[\, g_{\mu\nu}\, ]$ の逆行列 $[\, g^{\mu\nu}\, ]$ を使うと

\begin{align} 
	\vbdu{E}{a}{\mu} = g^{\mu\nu} \mathring{g}_{ab} \vbud{e}{b}{\nu}
\end{align}

であることがわかります．共役計量に対しては

\begin{align} 
	g^{\mu\nu} = \mathring{g}^{ab} \vbdu{E}{a}{\mu} \vbdu{E}{b}{\nu}
\end{align}

です．

正規直交標構

$\bigl\{ \hat{e}_a \bigr\}$ は正規直交系を成します：

\begin{align} 
	g_p[\hat{e}_a,\, \hat{e}_b] = \vbdu{E}{a}{\mu} \vbdu{E}{b}{\nu} g_p \left[ \pdv{}{x^{\mu}},\, \pdv{}{x^{\nu}} \right] = g_{\mu\nu} \vbdu{E}{a}{\mu} \vbdu{E}{b}{\nu} = \mathring{g}_{ab}.
\end{align}

この意味で $\{\, \hat{e}_a\, \}$ と $\{\, \hat{\theta}^a\, \}$ を正規直交標構 (orthonormal frame) と呼びます．

正規直交標構$\{\, \hat{\theta}^a\, \}$ を用いて $\bigwedge^k(T_p^*M)$ の基底を

\mathcal{O} := \bigl\{ \hat{\theta}^{i_1} \wedge \cdots \wedge \hat{\theta}^{i_k} \bigm| 1 \le i_1 < \cdots < i_k \le n \bigr\}

とすると，$\mathcal{O}$ は正規直交基底になります．

Hodge star

ここまででようやくHodge starを定義する準備が整いました．この節では $M$ を $n$ 次元向き付け可能多様体とします．ここで

\dim \bigwedge^k(T^*_p M) = \dim \bigwedge^{n-k}(T^*_p M)

であったことを思い出しましょう．つまり，これら二つは抽象ベクトル空間として同型です．Hodge starはまさに，多様体の各点 $p$ においてこの同型写像を与えてくれます．

正規直交標構における定義

例の如く，まずは一点 $p \in M$ を固定して，そこで正の向きの正規直交標構⁷ $\onf{1},\, \dots,\, \onf{n} \in T_p^*M$ をとります．微分形式は内在的 (intrinsic) に定義されており，チャートの取り方に依存しないので，正規直交標構を与える特定のチャートにおいてきちんと構成できればそれで十分です．

さて，作りたいのは

\star_p \colon \bigwedge^k(T^*_p M) \xrightarrow{\cong} \bigwedge^{n-k}(T^*_p M)

です．一番端の $k = 0$ の場合から攻めていきます．

$\bigwedge^0(T^*_p M) = \mathbb{R}$ なので正の向きの基底は $1$ で，

    \star_p 1 := \onf{1} \wedge \onf{2} \wedge \cdots \wedge \onf{n}

と定義すれば良いです．$n$-形式 $\star_p 1 \in \bigwedge^n(T^*_p M)$ のことを $M$ の体積要素 (volume element) と呼び，$\mathrm{vol}_M$ と書きます．

一般の $k$ に対しては，

\star_p (\onf{1} \wedge \cdots \wedge \onf{k}) := \left( \prod_{a=1}^k \pair{\onf{a}}{\onf{a}} \right) \onf{k+1} \wedge \cdots \wedge \onf{n}

と定義します．特に

    \prod_{a=1}^k \pair{\onf{a}}{\onf{a}} = \prod_{a=1}^k \mathring{g}^{aa}

とも書けます．Riemann多様体の場合これは常に $1$ なので気にしなくて良いですが，計量の対角成分に $-1$ が並ぶ擬Riemann多様体の場合は注意が必要です．

これが同型写像になっていることを確認します．そのためには $\star_p$ によって $ \bigwedge^k\bigl(T_p^* M\bigr) $ の基底が $ \bigwedge^{n-k}\bigl(T_p^* M \bigr) $ の基底に重複なく移ることを確認すれば良いです．

$\bigwedge^k(T^*_p M)$ の全ての基底は $\star(\theta^{\mu_1} \wedge \cdots \wedge \theta^{\mu_k})$ の形をしていますから，添字集合 $\{1,\, \dots ,\, n\}$ の部分集合（添字が小さい順に並んでいます） $I = \{ \mu_1,\, \dots ,\, \mu_k \}$ の補集合を小さい方から順に並べ>た添字の集合 $J = \{ \nu_1,\, \dots ,\, \nu_{n-k} \mid 1 \le \nu_1 < \cdots < \nu_{n-k} \le n\} $ を考えると

  \begin{align} 
  	\star_p(\theta^{\mu_1} \wedge \cdots \wedge \theta^{\mu_k}) 
= \mathrm{sgn} 
\begin{pmatrix} 1 & \dots & k & k+1 & \dots & n \\ \mu_1 & \dots & \mu_k & \nu_1 & \dots & \nu_{n-k} \end{pmatrix} 
\left(\prod_{a=1}^k \pair{\theta^{\mu_a}}{\theta^{\mu_a}}>\right)\, \theta^{\nu_1} \wedge \cdots \wedge \theta^{\nu_{n-k}}
  \end{align}

となります．添字集合 $I$ が異なるならば $J$ も異なるのでOKです．

基底の変換式はLevi-Civita記号とEinsteinの規約を併用した

	\begin{align} 
		\frac{1}{(n-k)!}\, \pair{\theta^{\mu_1}}{\theta^{\nu_1}} \cdots \pair{\theta^{\mu_k}}{\theta^{\nu_k}}\, \epsilon_{\nu_1 \dots \nu_k\nu_{k+1} \dots \nu_{n}}\, \theta^{\nu_{k+1}} \wedge \cdots \wedge \theta^{\nu_{n}}
	\end{align}

に等しいです⁸．いちいちこのように書くのは大変なので，Levi-Civita記号の添字の上げを $\mathring{g}^{\mu\nu} := \pair{\theta^\mu}{\theta^\nu}$ によって行って次のように略記します：

	\begin{align} 
		\epsilon^{\mu_1 \dots \mu_k}{}_{\nu_{k+1} \dots \nu_{n}} := \, \mathring{g}^{\mu_1\nu_1} \cdots \mathring{g}^{\mu_k\nu_k}\epsilon_{\nu_1 \dots \nu_k\nu_{k+1} \dots \nu_{n}}
	\end{align}

あとは $\star_p$ を $\forall p \in M$ に関して $C^\infty$ 級に繋げてHodge star

\star \colon \Omega^k(M) \longrightarrow \Omega^{n-k}(M)

の完成です．
$C^\infty$ 級に繋げることはあまり自明でないような気がするので一応確認しておきます．

$\forall \omega \in \Omega^k(M)$ を点 $p$ において正規直交標構で表示して

\omega_p = \omega_{\mu_1 \dots \mu_k}(p) \onf{\mu_1} \wedge \cdots \wedge \onf{\mu_k}

だったとすると，先程計算した基底の変換式から

\begin{align}
   \star_p \omega_p &= \omega_{\mu_1 \dots \mu_k}(p) \onf{\mu_1} \wedge \cdots \wedge \onf{\mu_k} \\
   &= \frac{1}{(n-k)!} \omega_{\mu_1 \dots \mu_k}(p) \epsilon^{\mu_1 \dots \mu_k}{}_{\nu_{k+1} \dots \nu_{n}}
   \onf{\nu_{k+1}} \wedge \cdots \wedge \onf{\mu_{n}}
\end{align}

ですが，$\omega$ が $C^\infty$ 切断であることから $\omega_{\mu_1 \dots \mu_k}(p) \in C^\infty(M)$ なので $\star \omega$ も$C^\infty$ 級です．

Hodge star の性質

$\forall f,\, g \in C^\infty(M)$ および $\forall \omega,\, \eta \in \Omega^k(M)$ に対して以下が成立します：

1. $\star (f\omega + g \eta) = f, \star \omega + g, \star \eta$
2. $\star \star \omega = (-1)^{k(n-k)} \omega$
3. $\omega \wedge \star \eta = \eta \wedge \star \omega = \pair{\omega}{\eta} \mathrm{vol}_M$
4. $\pair{\star \omega}{\star \eta} = \pair{\omega}{\eta}$

1 から，$\star$ が $C^\infty$ 加群としても同型写像であることを意味します．2 から

\star^{-1} = (-1)^{k(n-k)} \star

がわかります．ただしこれはRiemann多様体の場合で，計量の指数が $(i,, j)$ であるような擬Riemann多様体の場合は

\star^{-1} = (-1)^{j+k(n-k)} \star

です．
3 をHodge starの定義にすることもあります．先程の定義と 3 は同値です．
4 は $\star$ が $k$-形式の内積を保存することを意味します．これもRiemann多様体の場合限定で，計量の指数が $(i,\, j)$ であるような擬Riemann多様体の場合は

\pair{\star \omega}{\star \eta} = (-1)^j\pair{\omega}{\eta}

となります．

自然基底での表示

微分形式は内在的，i.e. 局所座標によらないなので，前節の定義でも十分ではあります．しかし，やはり双対基底における表示を求めておいた方が実用上便利です．

まずは体積要素を求めましょう．便宜上 $g := \det [g_{\mu\nu}]$ とおいておきます．

2つの正の向きのチャート $(U;\, x^\mu),\; (V;\, y^\nu)$ をとります．このとき

\begin{align}
\dd{x^1} \wedge \cdots \wedge \dd{x^n} &= \left( \pdv{x^1}{y^{\nu_1}} \dd{y^{\nu_1}} \right) \wedge \cdots \wedge \left(\pdv{x^n}{y^{\nu_n}} \dd{y^{\nu_n}} \right) \\
&= \pdv{x^1}{y^{\nu_1}} \cdots \pdv{x^n}{y^{\nu_n}} \epsilon_{\nu_1 \dots \nu_n} \dd{y^1} \wedge \cdots \wedge \dd{y^n} \\
&= \det \left[\pdv{x^\mu}{y^\nu} \right]_{\mu\nu} \dd{y^1} \wedge \cdots \wedge \dd{y^n}
\end{align}

です．ここでチャート $(U;\, x^\mu)$ を正の向きの正規直交標構 $\{\onf{\mu}\}$ に対応するチャートにとります．するとJacobi行列 $\det \left[\pdv{x^\mu}{y^\nu}\right]_{\mu\nu}$ は多脚場 $[\vbud{e}{\mu}{\nu}]$ に等しく，

g = \det \bigl([\vbud{e}{a}{\mu}][\mathring{g}_{ab}][\vbud{e}{b}{\nu}]) = \bigl( \det [\vbud{e}{\mu}{\nu}] \bigr)^2

正の向きのチャートを取っていたので

\sqrt{g}\dd{y^1} \wedge \cdots \wedge \dd{y^n} = \dd{\onf{1}} \wedge \cdots \wedge \dd{\onf{n}} = \mathrm{vol}_M

になります．擬Riemann多様体の場合は $\sqrt{\abs{g}}$ に変えれば良いです．この式は任意の座標系で成り立つので，

\mathrm{vol}_M = \sqrt{\abs{g}}\dd{y^1} \wedge \cdots \wedge \dd{y^n}

のことを不変体積要素とも言います．

次に，Hodge starの性質3 を用いて $k$ 形式の基底

\dd{x^{\mu_1}} \wedge \cdots \wedge \dd{x^{\mu_k}}

に対する $\star$ の作用を計算します．

\begin{align} 
	&(\dd{x^{1}} \wedge \cdots \wedge \dd{x^k}) \wedge \star (\dd{x^1} \wedge \cdots \wedge \dd{x^k}) \\
	&= \det \bigl( \, \pair{\dd{x^\mu}}{\dd{x^\nu}}\, \bigr)_{1 \le \mu,\, \nu \le k} \sqrt{\abs{g}} \dd{x^1} \wedge \cdots \wedge \dd{x^n} \\
	&= \det \bigl( g^{\mu\nu} \bigr)_{1 \le \mu,\, \nu \le k} \sqrt{\abs{g}} \dd{x^1} \wedge \cdots \wedge \dd{x^n}
\end{align}

なので，

\begin{align} 
	&\star (\dd{x^1} \wedge \cdots \wedge \dd{x^k}) \\
    &= \det \bigl( g^{\mu\nu} \bigr)_{1 \le \mu,\, \nu \le k} \sqrt{\abs{g}}\, \dd{x^{k+1}} \wedge \cdots \wedge \dd{x^n} \\
	&= \sqrt{\abs{g}}\, \epsilon_{\mu_1 \dots \mu_k} g^{\mu_1 1} \cdots g^{\mu_k k}\, \dd{x^{k+1}} \wedge \cdots \wedge \dd{x^n} \\
	&= \frac{\sqrt{\abs{g}}}{(n-k)!}\, \epsilon^{1 \dots k}{}_{\nu_{k+1} \dots \nu_{n}} \, \dd{x^{\nu_{k+1}}} \wedge \cdots \wedge \dd{x^{\nu_n}}.
\end{align}

ただし2番目の等号において，添字 $\{ \nu_{k+1},\, \dots \nu_{n}\}$ に関する和をとるようにしたことで重複する項が $(n-k)!$ 個出現するため，$(n-k)!$ で全体を割っています．$\{1,\, \dots ,\, k\}$ の順番を入れ替えることで

\begin{align} 
	\star (\dd{x^{\mu_1}} \wedge \cdots \wedge \dd{x^{\mu_k}}) = \frac{\sqrt{\abs{g}}}{(n-k)!}\, \epsilon^{\mu_1 \dots \mu_k}{}_{\nu_{k+1} \dots \nu_{n}} \, \dd{x^{\nu_{k+1}}} \wedge \cdots \wedge \dd{x^{\nu_n}}
\end{align}

と求まりました．

Hodge star の応用

3次元Riemann多様体 $M$ において，微分形式の外微分とHodge starと音楽同型をうまく組み合わせると，ベクトル解析で頻出の，一般曲線座標系における種々の微分演算子の計算が驚くほど簡単に実行できます．もう積の微分やら連鎖律やらに悩まされる必要はありません．

ベクトル場の勾配・回転・発散

勾配 $\mathrm{grad}$，回転 $\mathrm{rot}$，発散 $\mathrm{div}$ は，微分形式の外微分をHodge star と音楽同型を用いてベクトル場の世界で表現したものに他なりません．音楽同型，外微分，Hodge starはそれぞれ

\begin{align}
    \flat &\colon \mathfrak{X}(M) \longrightarrow \Omega^1(M) \\
    \sharp=\flat^{-1} &\colon \Omega^1(M) \longrightarrow \mathfrak{X}(M) \\
    \dd{} &\colon \Omega^k(M) \longrightarrow \Omega^{k+1}(M) \\
    \star &\colon \Omega^k(M) \longrightarrow \Omega^{3-k}(M)
\end{align}

で，これらを図式にすると

のようになります．まず $\flat$ でベクトル場を微分形式にしてから $\dd{}$ で上がった次数を $\star$ を用いてうまく調節して $\sharp$ でベクトル場に戻ってくるというイメージです． $3-2 = 1$ なのでこれで上手くいきます．従って，ベクトル場 $F \in \mathfrak{X}(M)$ に対して

\begin{align}
\mathrm{grad}\mathop{} F&= (\dd{F})^\sharp\\
\mathrm{rot}\mathop{} F &= (\star \dd{\star(F^\flat)})^\sharp \\
\mathrm{div}\mathop{} F &= \star \dd{} \star F^\flat
\end{align}

を計算すれば求める答えになります．

計算例

円筒座標

円筒座標 $(r,\, \phi,\, z)$ の計量は，前の方で紹介した誘導計量の方法で計算すると $[g_{\mu\nu}] = \mathrm{diag}\mathop{}\bigl( 1,\, r^2,\, 1 \bigr)$ です．双対基底のHodge starを計算すると

\begin{align}
    \star(\dd{r}) &= r \dd{\phi} \wedge \dd{z}, \\
    \star(\dd{\phi}) &= \frac{1}{r} \dd{z} \wedge \dd{r}, \\
    \star(\dd{z}) &= r \dd{r} \wedge \dd{\phi}, \\
    \star(\dd{r} \wedge \dd{\phi}) &= \frac{1}{r} \dd{z}, \\
    \star(\dd{\phi} \wedge \dd{z}) &= \frac{1}{r} \dd{r}, \\
    \star(\dd{z} \wedge \dd{r}) &= r \dd{\phi}
\end{align}

になります．

自然基底がすでに正規直交基底を成しているので，正規直交標構 $\hat{e}_{\mu}$ と自然基底場 $\partial_\mu$ は

\begin{align}
    \partial_r = \hat{e}_r,\; \partial_\phi = r\hat{e}_\phi,\; \partial_z = \hat{e}_z
\end{align}

の関係にあります．

ベクトル解析に登場するベクトル場の成分は，基本的に自然基底 $\partial_\mu$ による表示ではなく正規直交標構による表示です（physical component⁹）

今興味があるのは，スカラー場 $f \in C^\infty(M)$ の勾配および
ベクトル場 $F \in \mathfrak{X}(M)$ の正規直交標構による表示

\begin{align}
    F = F^r \hat{e}_r + F^\phi \hat{e}_\phi + F^z \hat{e}_z = F^r \partial_r + \frac{F^\phi}{r} \partial_\phi + F^z \partial_z
\end{align}

の回転・発散です．

勾配は即座に

\begin{align}
    \mathrm{grad}\mathop{} f &= g^{rr} \pdv{f}{r} \partial_r + g^{\phi\phi} \pdv{f}{\phi} \partial_\phi + g^{zz} \pdv{f}{z} \partial_z \\
    &= \pdv{f}{r} \hat{e}_\phi + \frac{1}{r} \pdv{f}{\theta} \hat{e}_\phi + \pdv{f}{z} \hat{e}{z}
\end{align}

となります．回転は，丁寧に書くと

\begin{align}
    \mathrm{rot}\mathop{} F &= \bigl[ \star\dd{F}^\flat\bigr]^\sharp \\
    &= \left[ \star \dd{\left( g_{rr} F^r \dd{r} + g_{\phi\phi} \frac{F^\phi}{r} \dd{\phi} + g_{zz} F^z \dd{z} \right)}  \right]^\sharp \\
    &= \left[ \star \dd{\left( F^r \dd{r} + r F^\phi \dd{\phi} + F^z \dd{z} \right)}  \right]^\sharp \\
    &= \left[ \star \left( -\pdv{F^r}{\phi} \dd{r} \wedge \dd{\phi} + \pdv{F^r}{z} \dd{z} \wedge \dd{r} \right. \right.\\
    &\qquad + \pdv{(r F^\phi)}{r} \dd{r} \wedge \dd{\phi} - \pdv{(r F^\phi)}{z} \dd{\phi} \wedge \dd{z} \\
    &\qquad \left. \left. + \pdv{F^z}{\phi} \dd{\phi} \wedge \dd{z} - \pdv{F^z}{r} \dd{z} \wedge \dd{r}\right)  \right]^\sharp \\
    &= g^{zz}\left(\pdv{(rF^\phi)}{r}-\pdv{F^r}{\phi} \right)\frac{1}{r} \partial_z
    + g^{rr}\left(\pdv{F^z}{\phi} - \pdv{(r F^\phi)}{z}\right) \frac{1}{r} \partial_r
    + g^{\phi\phi}\left(\pdv{F^r}{z} - \pdv{F^z}{r} \right) r \partial_\phi \\
    &= \frac{1}{r}\left(\pdv{F^z}{\phi} - \pdv{(r F^\phi)}{z}\right) \hat{e}_r
    + \left(\pdv{F^r}{z} - \pdv{F^z}{r} \right) \hat{e}_\phi
    + \frac{1}{r} \left(\pdv{(rF^\phi)}{r}-\pdv{F^r}{\phi} \right) \hat{e}_z
\end{align}

発散も丁寧に書くと

\begin{align}
    \mathrm{div}\mathop{} F &= \star \dd{\star F^\flat} \\
    &= \star \dd{\star \left( F^r \dd{r} + r F^\phi \dd{\phi} + F^z \dd{z} \right) } \\
    &= \star \dd{\left( rF^r \dd{\phi} \wedge \dd{z}  + F^\phi \dd{z} \wedge \dd{r} + rF^z \dd{r} \wedge \dd{\phi} \right) } \\
    &= \star\left[ \left( \pdv{(rF_r)}{r} + \pdv{F_\phi}{\phi} + \pdv{(rF_z)}{z}  \right) \dd{r} \wedge \dd{\phi} \wedge \dd{z}  \right] \\
    &= \frac{1}{r}\left[\pdv{(rF_r)}{r} + \pdv{F_\phi}{\phi} + \pdv{(rF_z)}{z}  \right]
\end{align}

と求まります．

3次極座標

3次元極座標 $(r,\, \theta,\, \phi)$ の回転と発散も計算してみましょう．
計量は $[g_{\mu\nu}] = \mathrm{diag}\mathop{} \bigl(1,\, r^2,\, r^2 \sin^2 \theta\bigr)$ だから，双対基底のHodge starは

\begin{align}
    \star(\dd{r}) &= r^2 \sin\theta \dd{\theta} \wedge \dd{\phi}, \\
    \star(\dd{\theta}) &= \sin\theta \dd{\phi} \wedge \dd{r}, \\
    \star(\dd{\phi}) &= \frac{1}{\sin\theta} \dd{r} \wedge \dd{\theta}, \\
    \star(\dd{r} \wedge \dd{\theta}) &= \sin\theta \dd{\phi}, \\
    \star(\dd{\theta} \wedge \dd{\phi}) &= \frac{1}{r^2 \sin\theta} \dd{r}, \\
    \star(\dd{\phi} \wedge \dd{r}) &= \frac{1}{\sin\theta} \dd{\theta}
\end{align}

です．ベクトル場 $F$ の正規直交標構による成分表示を $F^r,\, F^\theta,\, F^\phi$ とおくと

\begin{align}
    F = F^r \dd{r} + \frac{F^\theta}{r} \dd{\theta} + \frac{F^\phi}{r\sin\theta} \dd{\phi}
\end{align}

と書けるので，勾配は

\begin{align}
    \mathrm{grad}\mathop{} f = \pdv{f}{r} \hat{e}_r + \frac{1}{r} \pdv{f}{\theta} \hat{e}_\theta + \frac{1}{r\sin\theta}\pdv{f}{\phi}
\end{align}

回転と発散は

\begin{align}
    \mathrm{rot}\mathop{} F 
    &= \left[ \star \dd{\left( F^r \dd{r} + r F^\theta \dd{\theta} + r\sin\theta F^\phi \dd{\phi} \right)}  \right]^\sharp \\
    &= \left[ \star \left( -\pdv{F^r}{\phi} \dd{r} \wedge \dd{\theta} + \pdv{F^r}{\phi} \dd{\phi} \wedge \dd{r} \right. \right.\\
    &\qquad + \pdv{(r F^\theta)}{r} \dd{r} \wedge \dd{\theta} - \pdv{(r F^\theta)}{\phi} \dd{\theta} \wedge \dd{\phi} \\
    &\qquad \left. \left. + \pdv{(r\sin\theta F^\phi)}{\theta} \dd{\theta} \wedge \dd{\phi} - \pdv{(r\sin\theta F^\phi)}{r} \dd{\phi} \wedge \dd{r}\right)  \right]^\sharp \\
    &= g^{\phi\phi}\left(\pdv{(rF^\theta)}{r}-\pdv{F^r}{\theta} \right)\sin\theta \partial_\phi \\
    &\quad + g^{rr}\left(\pdv{(r\sin\theta F^\phi)}{\theta} - \pdv{(r F^\theta)}{\phi}\right) \frac{1}{r^2 \sin\theta} \partial_r \\
    &\quad + g^{\theta\theta}\left(\pdv{F^r}{\phi} - \pdv{(r\sin\theta F^\phi)}{r} \right) \frac{1}{\sin\theta} \partial_\theta \\
    &= \frac{1}{r^2 \sin\theta}\left(\pdv{(r\sin\theta F^\phi)}{\theta} - \pdv{(r F^\theta)}{\phi}\right) \hat{e}_r \\
    &\quad + \frac{1}{r\sin\theta}\left(\pdv{F^r}{\phi} - \pdv{(r\sin\theta F^\phi)}{r} \right) \hat{e}_\theta \\
    &\quad + \frac{1}{r}\left(\pdv{(rF^\theta)}{r}-\pdv{F^r}{\theta} \right) \hat{e}_\phi, \\
    \mathrm{div}\mathop{} F 
    &= \star \dd{ \star \left( F^r \dd{r} + r F^\theta \dd{\theta} + r\sin\theta F^\phi \dd{\phi} \right)} \\
    &= \star \dd{\left( r^2 \sin\theta F^r \dd{\theta} \wedge \dd{\phi} + r\sin\theta F^\theta \dd{\phi} \wedge \dd{r} + r F^\phi \dd{r} \wedge \dd{\theta} \right)} \\
    &= \frac{1}{r^2 \sin\theta} \left[ \pdv{(r^2 \sin\theta F^r)}{r} + \pdv{(r\sin\theta F^\theta)}{\theta} + \pdv{(r F^\phi)}{\phi} \right] 
\end{align}

となります．

一般の直交曲線座標

$d \le n$ として $C^\infty$ はめ込み

\boldsymbol{r}(q^1,\, \dots,\, q^d) = 
\begin{bmatrix}
    x^1(q^1,\, \dots,\, q^d) \\
    \vdots\\
    x^n(q^1,\, \dots,\, q^d) \\
\end{bmatrix}

が与えられたとき，自然基底自体が直交系をなすならば，誘導計量の方法によって

[g_{\mu\nu}] = \mathrm{diag} \bigl[ (h_{(1)})^2,\, \dots ,\, (h_{(d)})^2 \bigr]

となるのでした．ただし，スケール因子をEuclidノルム $\abs{\cdot}$ を使って

    h_{(\mu)} := \left| \pdv{\boldsymbol{r}}{q^\mu} \right|

と定義しました．この状況だと，一般次元 $d$ （回転は $d = 3$）に対する勾配・発散の割と実用的な公式を導出することができます．

自然基底と正規直交標構の関係は

\pdv{}{q^\mu} = h_{(\mu)} \hat{e}_\mu

なので（Einsteinの規約は使いません），勾配は即座に

    \mathrm{grad}\mathop{} f = \sum_{\mu=1}^d \frac{1}{(h_{(\mu)})^2} \pdv{f}{q^\mu} h_{(\mu)} \hat{e}_\mu = \sum_{\mu=1}^d \frac{1}{h_{(\mu)}} \pdv{f}{q^\mu}\hat{e}_\mu

とわかります．発散は

\begin{align}
    \mathrm{div} \mathop{} F &= \star \dd{} \star \sum_{\mu=1}^d (h_{(\mu)})^2 \frac{F^\mu}{h_{(\mu)}} \dd{q^\mu} \\
    &= \star \dd{} \sum_{\mu=1}^d h_{(\mu)} F^\mu \frac{\sqrt{\abs{g}}}{(d-1)!} \sum_{\nu_1,\, \dots,\, \nu_{d-1}} \frac{1}{(h_{(\mu)})^2} \epsilon_{\mu\nu_1 \dots \nu_{d-1}} \dd{q^{\nu_1}} \wedge \cdots \dd{q^{\nu_{d-1}}} \\
    &= \frac{1}{(d-1)!} \star \sum_{\lambda} \sum_{\mu,\, \nu_2,\, \dots,\, \nu_{d}} \pdv{}{q^\lambda} \left(\frac{\sqrt{\abs{g}}}{h_{(\mu)}} F^\mu \right) \epsilon_{\mu\nu_2 \dots \nu_{d}} \dd{q^\lambda} \wedge\dd{q^{\nu_2}} \wedge \cdots \dd{q^{\nu_{d}}} \\
    &= \sum_{\mu=1}^d \pdv{}{q^\mu} \left( \frac{\sqrt{\abs{g}}}{h_{(\mu)}} F^\mu \right) \star \bigl( \dd{q^1} \wedge \dd{q^2} \wedge \cdots \wedge \dd{q^{d}} \bigr) \\
    &= \sum_{\mu=1}^d \frac{1}{\sqrt{\abs{g}}} \pdv{}{q^\mu} \left( \sqrt{\frac{\abs{g}}{g_{\mu\mu}}} F^\mu \right)
\end{align}

この公式は

\sqrt{\abs{g}} = \prod_{\mu=1}^d h_{(\mu)}

なのでかなり使いやすいです．

回転に関しては，Hodge starが

\begin{align}
    \star(\dd{q^1} \wedge \dd{q^2}) &= \frac{h_{(3)}}{h_{(1)}h_{(2)}} \dd{q^3} \\
    \star(\dd{q^2}\wedge \dd{q^3}) &= \frac{h_{(1)}}{h_{(2)}h_{(3)}} \dd{q^1} \\
    \star(\dd{q^3} \wedge \dd{q^1}) &= \frac{h_{(2)}}{h_{(3)}h_{(1)}} \dd{q^2}
\end{align}

であることを使うと

\begin{align}
    \mathrm{rot}\mathop{} F &= \sharp \left( \star \dd{} \sum_{\mu=1}^3 (h_{(\mu)})^2 \frac{F^\mu}{h_{(\mu)}} \dd{q^\mu}\right) \\
    &= \sharp \left( \star \sum_{\mu = 1}^3 \sum_{\nu=1}^3 \pdv{}{q^\nu} \bigl( h_{(\mu)} F^\mu \bigr) \dd{q^\nu} \wedge \dd{q^\mu}\right) \\
    &= \sharp\left[\left( \pdv{(h_{(2)} F^2)}{q^1} - \pdv{(h_{(1)} F^1)}{q^2} \right) \frac{h_{(3)}}{h_{(1)}h_{(2)}} \dd{q^3}\right. \\
    & \quad + \left( \pdv{(h_{(3)} F^3)}{q^2} - \pdv{(h_{(2)} F^2)}{q^3} \right) \frac{h_{(1)}}{h_{(2)}h_{(3)}} \dd{q^1} \\
    & \left. \quad + \left( \pdv{(h_{(1)} F^1)}{q^3} - \pdv{(h_{(3)} F^3)}{q^1} \right) \frac{h_{(2)}}{h_{(3)}h_{(1)}} \dd{q^2} \right]\\
    &= \left( \pdv{(h_{(3)} F^3)}{q^2} - \pdv{(h_{(2)} F^2)}{q^3} \right) \frac{1}{h_{(2)}h_{(3)}} \hat{e}_1 \\
    & \quad + \left( \pdv{(h_{(1)} F^1)}{q^3} - \pdv{(h_{(3)} F^3)}{q^1} \right) \frac{1}{h_{(3)}h_{(1)}} \hat{e}_2 \\
    & \quad +\left( \pdv{(h_{(2)} F^2)}{q^1} - \pdv{(h_{(1)} F^1)}{q^2} \right) \frac{1}{h_{(1)}h_{(2)}} \hat{e}_3
\end{align}

を得ます．

さらに一般の場合

計量が非対角項を含む場合であっても，自然基底による成分表示はすぐに求まります．これまでの計算はこれの特殊な場合にすぎません．
勾配は

\begin{align}
    \mathrm{grad}\mathop{} f = g^{\mu\nu} \pdv{f}{x^\mu} \partial_\nu 
\end{align}

回転は

\begin{align}
    \mathrm{rot}\mathop{} F &= \sharp \bigl( \star \partial_\mu (g_{\nu\lambda} F^\lambda) \dd{x^\mu} \wedge \dd{x^\nu}\bigr)  \\
    &= \sharp \bigl( \partial\mu(g_{\nu\lambda} F^\lambda) \sqrt{\abs{g}} g^{\mu\kappa} g^{\nu\rho} \epsilon_{\kappa\rho \sigma} \dd{x^\sigma}\bigr) \\
    &= \sqrt{\abs{g}} g^{\mu\kappa} g^{\nu\rho} g^{\alpha \sigma} \epsilon_{\kappa\rho\sigma} \partial_\mu (g_{\nu \lambda} F^\lambda) \partial_\alpha
\end{align}

発散は¹⁰

\begin{align}
    \mathrm{div}\mathop{} F &= \star \dd{} \star \bigl( g_{\mu\nu} F^\nu \dd{x^\mu} \bigr) \\
    &= \star \dd{} \left( g_{\mu\kappa} F^\kappa \frac{\sqrt{\abs{g}}}{(d-1)!} \epsilon^{\mu}{}_{\nu_2 \dots \nu_d} \dd{x^{\nu_2}} \wedge \cdots \wedge \dd{x^{\nu_d}}\right) \\
    &= \frac{1}{(d-1)!} \star \left[ \pdv{}{x^\lambda} \bigl( \sqrt{\abs{g}}  g^{\mu \nu} g_{\mu\kappa} F^\kappa \bigr) \epsilon_{\nu \nu_2 \dots \nu_d} \dd{x^\lambda} \wedge \dd{x^{\nu_2} \wedge \cdots \wedge \dd{x^{\nu_d}}}  \right] \\
    &= \pdv{}{x^\nu} \bigl( \sqrt{\abs{g}} F^\nu \bigr) \star \bigl(\dd{x^1} \wedge \dd{x^{2}} \wedge \cdots \wedge \dd{x^{d}} \bigr) \\
    &= \frac{1}{\sqrt{\abs{g}}} \pdv{}{x^\nu} \bigl( \sqrt{\abs{g}}  F^\nu \bigr) 
\end{align}

と求まります．

ラプラシアンの便利公式

最後に，ラプラシアンの計算方法について述べようと思います．

随伴外微分作用素 を次のように定義します：

\delta \colon \Omega^k(M) \longrightarrow \Omega^{k-1}(M),\; \omega \longmapsto (-1)^k \star^{-1} \dd{\star \omega}

一見わかりにくいですが，Hodge starの性質2を使うとRiemann多様体¹¹の場合

\delta = (-1)^{n(k+1)+1} \star \dd{\star}

になります．これを図式にすると次の通りです：

外微分とは逆に，微分形式の次数を下げる方向であることに注意です．そしてラプラシアンの一般化として

\Delta := \dd{\delta} + \delta \dd{} \colon \Omega^k(M) \longrightarrow \Omega^k(M)

と定義します．これはベクトル解析で登場するラプラシアンと $-1$ 倍を除いて一致します．

スカラー関数への $\Delta$ の作用を計算しましょう．$C^\infty(M) = \Omega^0(M)$ を思い出すと，スカラー関数に $\delta$ をかけると $0$ になってしまいます．よって，計算するべきは $\delta\dd{}$ です：

\begin{align}
    \Delta f &= - \star \dd{} \star \partial_\mu f \dd{x^\mu} \\
    &= - \star \dd{}\left(\frac{\sqrt{\abs{g}}}{(d-1)!} \partial_\mu f\, g^{\mu\lambda} \epsilon_{\lambda \nu_2\dots \nu_d} \dd{x^{\nu_2}} \wedge \cdots \wedge \dd{x^{\nu_d}}\right) \\
    &= - \star \frac{1}{(d-1)!} \partial_\nu \bigl( \sqrt{\abs{g}} g^{\lambda\mu} \partial_\mu f  \bigr) \epsilon_{\lambda\nu_1\dots \nu_d} \dd{x}^\nu \wedge \cdots \wedge \dd{x^\nu_d} \\
    &= - \partial_\nu \bigl( \sqrt{\abs{g}} g^{\nu\mu} \partial_\mu f \bigr) \star (\dd{x^1} \wedge \cdots \wedge \dd{x^d}) \\
    &= -\frac{1}{\sqrt{\abs{g}}} \partial_\nu \bigl( \sqrt{\abs{g}} g^{\nu\mu} \partial_\mu f \bigr) 
\end{align}

おわりに

なんとかHodge starの導入まで漕ぎ着けることができました．結局本記事ではちょっとした計算テクニックを紹介しただけですが，微分幾何学の本当に面白い世界はこれから先に広がっています．皆さんが微分幾何学の面白さを見出すきっかけになれたら幸いです．

参考文献

• John M. Lee (2012), Introduction to Smooth Manifolds, 2nd edition, Springer
• Tohru Eguchi, Peter B. Gilkey, Andrew J. Hanson (1980), Gravitation, gauge theories and differential geometry, Physics Reports
• David C. Kay (2011), Tensor Calculus, McGrow-Hill
• 森田茂之 (2005), 微分形式の幾何学, 岩波書店
• 中原幹夫 (2018), 理論物理学のための幾何学とトポロジーI, 原著第2版, 日本評論社

1. 埋め込みははめ込み(immersion)です．正確には，はめ込み $f \colon M\to N$ が埋め込みであるとは，$f$ が $M$ から $f(M)$ への同相写像になっている事を言います． ↩

2. この $*$ による対応は位相空間の圏から加群の圏への共変関手となっています． ↩

3. この命名は Lee (2012) の p.341 に載っていました．$g_{\mu\nu}$ の添字の半分（半音）を使って下げる（上げる）ので $\flat$（$\sharp$）ということなのかもしれない？ ↩

4. このようにして構成される対象は，底空間を $M$ とするベクトル束の $C^\infty$ 切断になります． ↩

5. 表現行列が $[g_{\mu\nu}]^{-1} = [g^{\mu \nu}]$ であるような双線型写像 $G_p$ ↩

6. 擬Riemann多様体の場合，対角要素に一つ以上の $-1$ が並びます．対角要素に $1$ が $i$ 個，$-1$ が $j$ 個並ぶ計量のことを指数 (index) $(i,, j)$ の計量と呼びます． ↩

7. とても雑に言うと，$\det [\vbud{e}{a}{\mu}] > 0$ ということです．詳細は微分幾何学の教科書を参照してください． ↩

8. Einsteinの規約により $n$ 個の添字について「無駄に」総和することになりますが，最初の $k$ 個に関しては $\pair{\onf{\mu}}{\onf{\nu}} = \mathring{g}^{\mu\nu}$ が対角型なので重複はないです．しかし，残りの $n-k$ 個の添字に関しては重複してしまうので，添字の並べ替えの総数である $(n-k)!$ で割る必要があります． ↩

9. この呼び方は D.C.Kay (2011) p.155 に倣っています． ↩

10. 式変形の途中で $A^\nu_{\lambda} \epsilon_{\nu \nu_1 \dots \nu_d} \dd{x^\lambda} \wedge \dd{x^{\nu_1}} \wedge \cdot \wedge \dd{x^{\nu_d}}$ のような和を計算する必要がありますが，Levi-Civita記号の反対称性から $\nu = \lambda$ 以外の項は0になることと，$\nu_2,, \dots ,, \nu_d$ に関して $(d-1)!$ 項の重複が出てくることに注意すれば良いです． ↩

11. 計量の指数が $(i,\, j)$ の擬Riemann多様体の場合 $(-1)^j$ さらにをかけます． ↩