ロジスティック回帰とは?
機械学習において様々なアルゴリズムが使われますが、今回紹介するロジスティック回帰も機械学習アルゴリズムの内の1つです。
ロジスティック回帰は回帰という名前がついていますが、2値分類のための学習アルゴリズムです。
パーセプトロンなどの線形モデルでは、出力を0か1のクラスとして決定していましたが、ロジスティック回帰では出力を確率として出します。
そしてその確率の値から2値分類を行います。
イメージとしては明日の天気を考える時に、降水確率が80%なら多分雨。降水確率が20%なら多分晴れ、という風な分類を行いますね。
これと同じことをロジスティック回帰ではやっています。
オッズ比とロジット関数
ロジスティック回帰を数式的に理解するためにまずはオッズ比とロジット関数という概念について説明していきます。
オッズ比
オッズ比とは予測したい事象が起こる確率をpとした時に、$\frac{p}{(1-p)}$という風に表されるものです。
分母の(1-p)は予測したい事象が起こらない確率のことなので、上で示したオッズ比というものは予測したい事象の起こりやすさを表しているのだと分かります。
ロジット関数
オッズ比について説明してきましたが、このオッズ比に自然対数をとったものをロジット関数と言います。
$${\rm logit}(p) = \log{\frac{p}{(1-p)}}$$
ロジット関数は0よりも大きく、1よりも小さい入力値を受け取り、実数全範囲の値に変換します。
ロジスティックシグモイド関数
ここでは上でした説明を踏まえて、ロジスティック回帰で使う活性化関数について説明していきます。
シグモイド関数の性質
上で解説したロジット関数の逆関数を考えてみましょう。
ロジット関数をzとおきます。
$$z = \log{\frac{p}{(1-p)}}
\\\mathrm{e}^{z} = \frac{p}{(1-p)}
\\p = \frac{\mathrm{e}^{z}}{\mathrm{e}^{z} + 1}
\\p = \frac{1}{1 + \mathrm{e}^{-z}}$$
上で導出された関数をロジスティックシグモイド関数、もしくはシグモイド関数と言います。
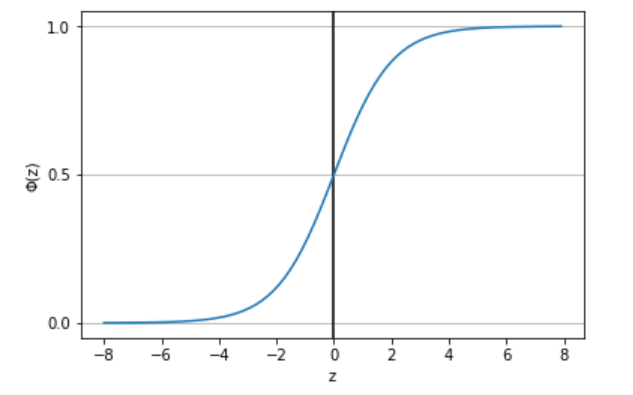
今、シグモイド関数を$\phi(z) = \frac{1}{1 + \mathrm{e}^{-z}}$とおき、グラフを描くと以下のようになります。
上のグラフを見たら分かるようにシグモイド関数では、入力として実数zを受け取り、出力を0から1の範囲で出しています。
つまり、確率として出力を出す、ロジスティック回帰アルゴリズムにおいてシグモイド関数を活性化関数として用いるのが最適であるということが分かります。
シグモイド関数による2値分類
それではシグモイド関数の入力zはどのように表されるか見ていきましょう。
zは以下のような式で表されます。
$$z=b+\sum^n_{i=1}w_ix_i$$
ここでwは重み、bはバイアス項です。
つまりzは重みと特徴量の線形結合に、バイアスを足し合わせたような値になっています。
これを入力としてシグモイド関数に入れると、0~1の値(確率)として出力されるということです。
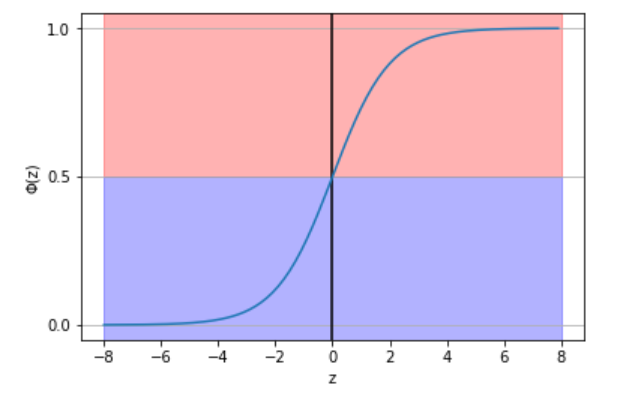
ロジスティック回帰は2値分類のアルゴリズムなので、0.5という値を境に0と1のクラスに分類します。
$$\hat{y} = \begin{cases}
1 & (\phi(z)\geq0.5) \\
0 & (\phi(z)<0.5)
\end{cases}$$
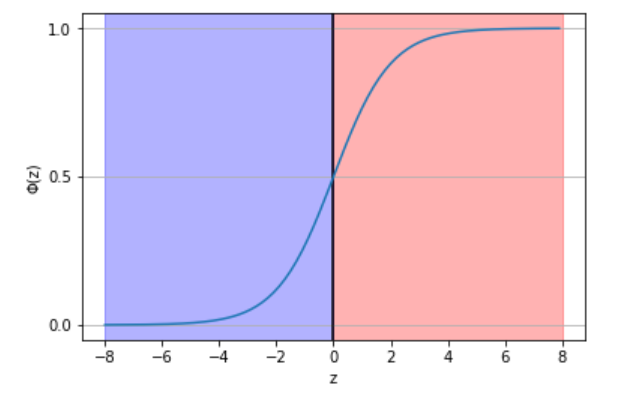
上のグラフを見ると分かると思いますが、以下のように書き換えることができます。
$$\hat{y} = \begin{cases}
1 & (z\geq0) \\
0 & (z<0)
\end{cases}$$
ロジスティック関数の重みの学習
ここまでの説明で、重みと特徴量の線形結合を総入力としてシグモイド関数に入れれば、0~1の値が確率として得られるという話をしましたが、もちろん0~1の値が出力されているからといって、予測したい事象の確率が出力されているということにはなりません。
ここでは尤度(結果から見たところの条件のもっともらしさ)という概念をを取り入れていきます。
尤度の最大化を考えることによって、予測したい事象の確率をより正確に出力できるようにします。
尤度Lは以下のように書けます。
$$L(w)=\prod_{i=1}^n P(y^{(i)}|x^{(i)};w)=\prod_{i=1}^n (\phi(z^{(i)}))^{y^{(i)}}(1-\phi(z^{(i)}))^{1-y^{(i)}}$$
積の形から和の形にして最大化しやすくします。
$$l(w)=\log{L(w)}=\sum_{i=1}^n [y^{(i)}\log(\phi(z^{(i)}))+(1-y^{(i)})\log(1-\phi(z^{(i)}))]$$
これを対数尤度関数と言います。
この尤度関数を最大化していくことによって最適な重みを見つけるのです。
参考文献
[Python機械学習プログラミング―達人データサイエンティストによる理論と実装][link]
[link]:https://www.amazon.co.jp/Python-%E6%A9%9F%E6%A2%B0%E5%AD%A6%E7%BF%92%E3%83%97%E3%83%AD%E3%82%B0%E3%83%A9%E3%83%9F%E3%83%B3%E3%82%B0-%E9%81%94%E4%BA%BA%E3%83%87%E3%83%BC%E3%82%BF%E3%82%B5%E3%82%A4%E3%82%A8%E3%83%B3%E3%83%86%E3%82%A3%E3%82%B9%E3%83%88%E3%81%AB%E3%82%88%E3%82%8B%E7%90%86%E8%AB%96%E3%81%A8%E5%AE%9F%E8%B7%B5-impress-gear/dp/4295003379/ref=pd_lpo_sbs_14_t_0?_encoding=UTF8&psc=1&refRID=NYR1ZQ8DE1AJ40BKARKG
機械学習をフワッと理解するのにおすすめの記事
[機械学習を猫でもわかるように説明してみた(教師あり学習と教師なし学習)][link2]
[link2]:https://city3939.com/machine-learning/