Pythonで書くフーリエ級数の検算用コード

理工系の学部生にとって厄介なのはフーリエ級数の手計算である。
一通り計算したはいいものの、結果が汚すぎて自信がないということはよくある。
そこでPythonで検算できるコードを書いたので備忘録も兼ねて掲載する。

例えば

f(x)=x \ \ \ \ (-\pi \le x \le \pi)

をフーリエ級数展開すると

f(x)=-\Sigma_{n=1}^{\infty}\frac{(-1)^n}{n}\sin(nx)

となる。これを検算してみよう。

import numpy as np
import matplotlib.pyplot as plt

#x軸を定義する
x = np.arange(-np.pi,np.pi,0.01)

#シグマの中身の関数
def func(k):
    return -1*(((-1)**k)/k)*np.sin(k*x)

#シグマ演算の関数. 引数で和の範囲を指定.
def sigma(func,frm,to):
    ret = np.zeros_like(x)
    for i in range(frm,to):
        ret += func(i)
    return ret

#フーリエ級数展開の関数
f = sigma(func,1,100)

#結果の表示
fig, ax = plt.subplots(1,1)
ax.set_aspect('equal')
ax.plot(x,f)
plt.show()

#こっちは足されていく過程をみるためのグラフ
#この設定では高々9回まで
"""
fig, axes = plt.subplots(3,3,figsize=(7,7))
for i,ax in enumerate(axes.ravel()):
    ax.set_aspect('equal')
    ax.set_title('n={}'.format(i))
    f = sigma(func,1,i)
    ax.plot(x,f)
plt.show()
"""

結果はこのようになる。

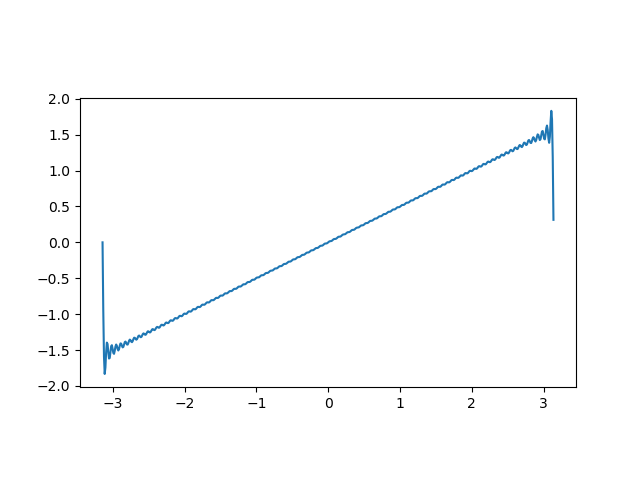
100個の項を足し合わせたものだが、そこそこ再現できている。

ついでにコード中でコメントアウトしている部分を実行すると結果は次のようになる。

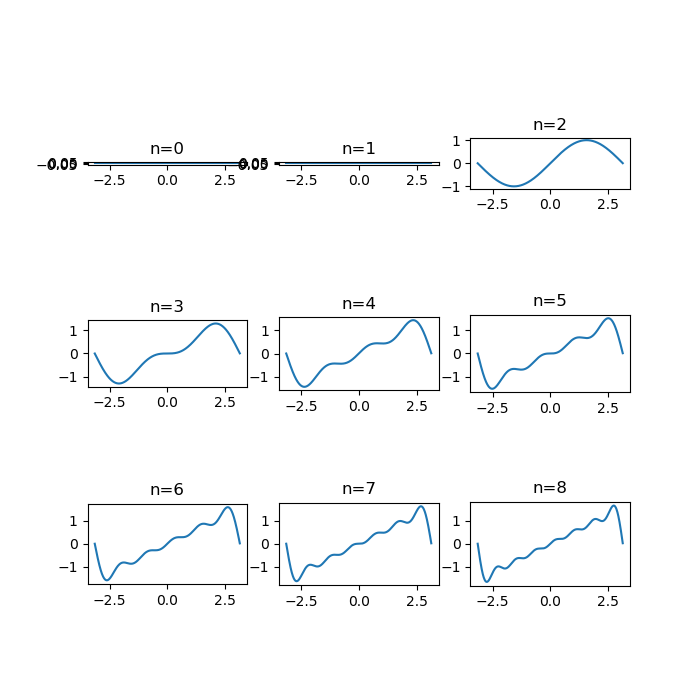
n=0,1についてはfor文の関係で表示されないが、ここは各々変更して欲しい。

参考文献