この記事は「文字列アルゴリズム Advent Calendar 2017」19日目の記事です.
はじめに
@goonewによる4日目の記事「Compact Directed Acyclic Word Graphを定義する」で紹介されている DAWG を用いたアルゴリズムなのでそちらの記事を先に読んでいるとわかりやすいかもしれません.
でもそんなに深いお話はしないので,この記事を読むだけで十分であればいいなと思います.
この記事では DAWG の細かい説明は行わないので気になった場合は参照してみてください.
準備
文字列に関する記法の導入や今回用いる用語の定義を行います.
基本的にこちらの記法を用いていますので,文字列の基本的な表記や用語に慣れ親しんでいない方はまずはご一読ください.
文字列 $T$ に含まれる文字の集合を $\Sigma_T$,文字列 $T$ の部分文字列の集合を $\mathit{Factor}(T)$ と表します.
また $T$ 自身を除く部分文字列のことを真の部分文字列と呼びます.
つまり真の部分文字列の集合は $\mathit{Factor}(t) \backslash \{T\}$ となります.
Minimal absent word (MAW)
文字列 $T$ 中に文字列 $x$ が出現しないとき, $x$ を $T$ の absent word と呼びます.今回は簡単のために,$x$ は $\Sigma_T$上の文字列とします.
例えば,$T=\mathtt{aabbabaa}$ のとき $x=\mathtt{abab}$ は $T$ の absent word なわけです.
特に absent word $x$ に対して,$x[2,|x|]$ と $x[1,|x|-1]$ が $T$ の部分文字列であるとき $x$ を $T$ の minimal absent word (MAW) といいます.
特に absent word $x$ に対して,$x$ の真の部分文字列が $T$ の部分文字列であるとき $x$ を $T$ の minimal absent word (MAW) といいます.例えば $T=\mathtt{aabbabaa}$ 中に $x=\mathtt{abab}$ は出現せず,真の部分文字列 $\epsilon,\mathtt{a,b,ab,ba,aba,bab}$ はそれぞれ出現しているので,$x$ は $T$ の minimal absent word です.

文字列 $T$ のすべての minimal absent word の集合を $\mathit{MAW}(T)$ と表します.
ちなみに $\mathit{MAW}(\mathtt{aabbabaa})$ は $\{\mathtt{aaa,bbb,aaba,baab,babb,bbaa} \}$ となります.
「すべての真の部分文字列が出現する」ということを確認するのは少々骨が折れますね.
長さ4の文字列 $\mathtt{abab}$ ですら6種類の真の部分文字列が存在します.
長さ$n$ の文字列に対しては最悪 $n(n+1)/2-1$種類の真の部分文字列が存在します.
やってられません.
そこで以下のように考えます.
$x$ が MAW である $\leftrightarrow$ $x \notin \mathit{Factor}(T)$ かつ $x[2,|x|],x[1,|x|-1]\in \mathit{Factor}(T)$
これは $x$ の真の部分文字列が,必ず $x[2,|x|]$ または $x[1,|x|-1]$ の部分文字列になっていることから明らかですね.これなら骨が折れずに済みそうです.

つまり $ayb~(a,b\in \Sigma, y \in \Sigma^*)$ に対して,「$ayb$ は $T$ の MAW $\leftrightarrow$ $ayb\notin \mathit{Factor}(T)$ かつ $ay, yb \in \mathit{Factor}(T)$」となります.
(今回は absent word を $\Sigma_T$ 上の文字列としているため,長さ 1 の MAW は存在しません.)
Directed acyclic word graph (DAWG)
文字列の接尾辞のみを受理する状態数最小の決定性有限オートマトンを Directed acyclic word graph (DAWG) といいます.
初期状態から $T$ の部分文字列 $x$ で遷移した先の状態を,$x$ に対応する状態と呼びます.
状態と文字列は一対一対応ではなく,一つの状態に複数の文字列が対応している事があります.
ある状態に対応する文字列のうち,最短のものを $\mathit{label}(u)$ と表します.
また,状態 $u$ から,$\mathit{label}(u)[2,|\mathit{label}(u)|]$ に対応する状態 $v$ へ suffix link と呼ばれる有向辺があります.
下図は $T=\mathtt{aabbabaa}$ の DAWG,$\mathit{DAWG}(T)$ です.
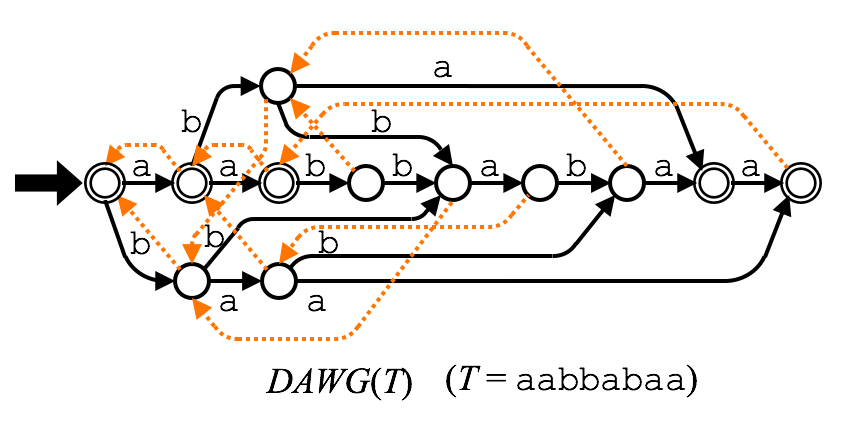
破線は suffix link を表します.
$\mathit{DAWG}(T)$ に対して
$x \in \mathit{Factor}(T) \leftrightarrow x$ に対応する状態が存在する
が成り立ちます.
$\mathit{DAWG}(T)$ の領域計算量は $O(|T|)$ です.
MAWの計算アルゴリズム
文字列 $T$ に対する DAWG が与えられた際に,$\mathit{MAW}(T)$ を $O(|T|+|\mathit{MAW}(T)|)$時間・$O(1)$追加領域で計算するアルゴリズムを紹介します.
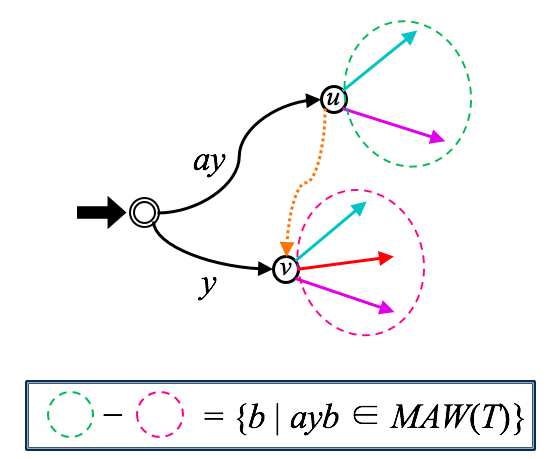
基本的なアイディアは $T$ の部分文字列 $ay$ に対して,$ayb \notin \mathit{Factor}(T)$ かつ $yb \in \mathit{Factor}(T)$ を満たす文字 $b$ を見つけていくことです.
これらの条件を満たす文字列 $ayb$ を $T$ に関する DAWG を用いて列挙していきます.
つまり,$T$ の各部分文字列 $ay$ に対して, DAWG上で$y$ に対応する状態からは遷移できるが,$ay$ に対応する状態からは遷移できない文字 $b$ を探索していきます.
すべての部分文字列 $ay$ に対してこれを満たすような文字 $b$ を見つけるのは明らかに無駄な時間がかかってしまいます.なので,MAW $ayb$ に関して $ay$ が満たす性質を考えていきましょう.
もし $ay$ と $y$ に対応する状態が一致する場合,その状態から遷移することの出来る文字の集合は当然ながら一致します.
したがって,$ayb$ が MAW となるとき,$ay$ と $y$ それぞれに対応する DAWG の状態は一致しないことがわかります.
したがって,$ay = \mathit{label}(u)$ となる状態 $u$ が必ず存在しており,このとき明らかに $y$ は $u$ の suffix link 先の状態 $v$ に対応しています.
考えるべき部分文字列は $ay = \mathit{label}(u)$ となる $u$ が存在するような $ay$ に絞られました.
これは DAWG の初期状態以外の状態と一対一対応します.
したがってすべての状態 $u$ に対して,$u$ と suffix link 先の状態 $v$ の出次辺の差分を計算すれば $\mathit{MAW}(T)$ を出力することが出来ます.
簡単ですね.
下の例を御覧ください.
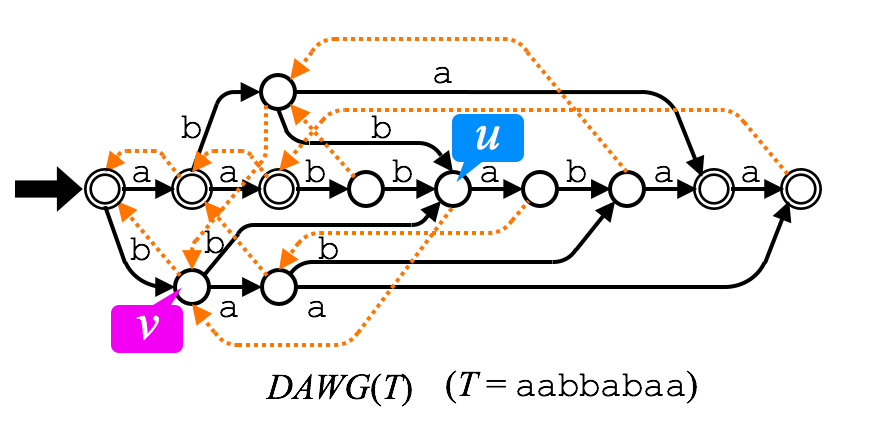
状態 $u$ からは $\{\mathtt{a}\}$ で遷移することができ,$v$ からは $\{\mathtt{a,b}\}$ で遷移することができます.したがって,$v$ でのみ遷移できる文字は $\mathtt{b}$ なので,$\mathit{label}(u)\mathtt{b} = \mathtt{bbb}$ は $T$ の MAW の一つとなります.
同様の計算をすべての状態 $u$ に対して行えばいいのです.
このときの計算量はどうなるのでしょうか.
各頂点 $u$ に対して,差分の計算にかかる時間は,「状態 $v$ の出次数」で押さえられます.これは「頂点 $u$ の出次数 + 出力の数」と一致しますので,全体で $O(|T|+|\mathit{MAW}(T)|)$ 時間で列挙できるわけです.
最後に
DAWG が与えられた際の MAW の計算アルゴリズムについてお話いたしました.
入力として文字列が与えられた際には DAWG を構築してから MAW を求めることとなります.
文字列 $T$ に対する DAWG を構築する時間を $D_T$ とすると,入力が文字列 $T$ だった際に MAW を列挙するのにかかる時間は $O( D_T +|T|+|\mathit{MAW}(T)|)$ となります.
$D_T$がいくらになるのかは,アルファベットの仮定によって異なります.
これらの内容は以下の論文にまとめられていますので,興味を持った方は是非読んでみてください.
- Yuta Fujishige, Yuki Tsujimaru, Shunsuke Inenaga, Hideo Bannai, Masayuki Takeda:
Computing DAWGs and Minimal Absent Words in Linear Time for Integer Alphabets. MFCS 2016: 38:1-38:14 link