Pythonで数値計算プログラムを書き直そうシリーズ
間違っていたら教えてください(土下座)
はじめに
高校などで区分求積法を学びますが、微小区間の定積分値を長方形で近似するのではなく、台形で近似して計算するのが台形則の手法です。本当にただ台形の面積を求めて足し合わせるだけです。
[Pythonによる科学・技術計算] 数値積分, 台形則・シンプソン則,数値計算, scipy
数値積分
Python - 数値積分 台形法 & シンプソン法
完成したプログラム
# 台形公式による数値積分プログラム
import numpy as np #NumPyライブラリ
import matplotlib.pyplot as plt #データ可視化ライブラリ
# 定積分したい関数
def func_f(x):
return 3.0*x**2.0
# 台形公式で定積分を計算(関数、定積分の開始点、定積分の終了点、刻み幅)
def trapezoidal(func_f, x_min, x_max, dx=1e-2):
num_calc = 0 #計算回数
x_div = (x_max-x_min)/dx #格子分割数
x = x_min #独立変数t
y = func_f(x) #従属変数y
print("x = {:.7f}, y = {:.7f}".format(x, y))
#グラフ用データを追加
x_list = [x]
y_list = [y]
#x = x_min
area = 0.0 #積分値(面積)
while(True):
num_calc += 1 #計算回数を数える
x += dx
delta_area = (func_f(x-dx) +func_f(x))*dx/2.0
area += delta_area
#グラフ用データを追加
x_list.append(x)
y_list.append(func_f(x))
#「計算回数が格子分割数以上」ならば終了
if(x_div<=num_calc):
break
#「計算回数が閾値以上」かつ「面積が微小」ならば終了
#if(x_div/2.0<=num_calc and delta_area<=1e-10):
#break
print("n = {:3d}: area = {:.15f}".format(num_calc, area))
return area, x_list, y_list
# 可視化
def visualization(func_f, area, x_list, y_list):
plt.xlabel("$x$") #x軸の名前
plt.ylabel("$f(x)$") #y軸の名前
plt.grid() #点線の目盛りを表示
plt.axhline(0, color='#000000') #f(x)=0の線
#関数
exact_x = np.arange(x_list[0],x_list[-1], (x_list[-1]-x_list[0])/500.0)
exact_y = func_f(exact_x)
plt.plot(exact_x,exact_y, label="$y(t)$", color='#ff0000') #折線グラフで表示
plt.fill_between(x_list,y_list, alpha=0.2) #塗りつぶし
plt.text(x_list[0],y_list[0], "$x$ = {:.9f}".format(area), va='bottom', color='#0000ff')
plt.show() #グラフを表示
# メイン実行部
if (__name__ == '__main__'):
#台形公式で定積分を求める
area, x_list, y_list = trapezoidal(func_f, -1.0, 1.0)
#結果を可視化
visualization(func_f, area, x_list, y_list)
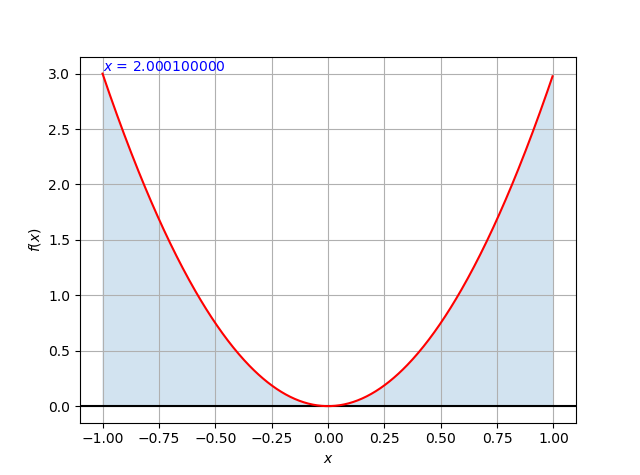
主なアルゴリズムはtrapezoidal関数に書きました。引数として、方程式の関数項f(x)、定積分の開始点、定積分の終了点を渡します。オプションとして、刻み幅を変えることもできます。戻り値は、定積分値、独立変数のリスト、関数値のリストです。上のプログラムでは$y = 3x^2$について、$-1 <= x <= 1$の範囲で定積分しています。数値積分の領域は、グラフの青色部分で示しています。
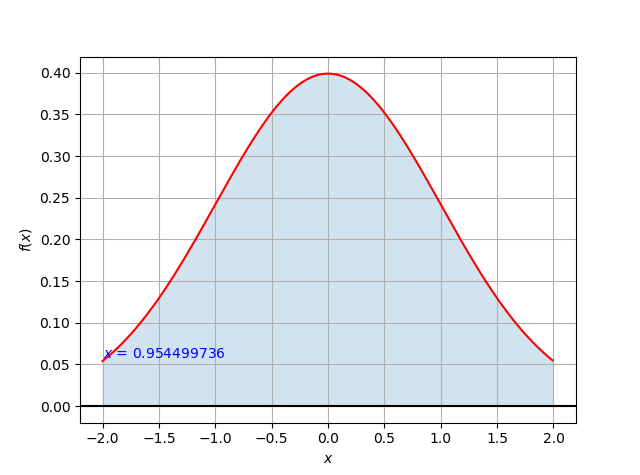
個人的にモジュールとして呼び出し可能にしたかったので、そういう構造になっています。モジュールとして使うテストプログラムは以下に書きました。$y = \frac{1}{\sqrt{2 \pi}} \exp(-\frac{x^2}{2})$と、$y = \frac{\sin(x)}{x}$の場合で計算しています。前者の式は、平均1、分散1の正規分布を表しています。また後者の式では、$\frac{\sin(0)}{0}$が計算できずにエラーとなります。
import numpy as np #数値計算用モジュール
import trapezoidal
# 標準正規分布
def func_f1(x):
return 1.0/np.sqrt(2.0*np.pi)*np.exp(-x**2.0/2.0)
area1, x_list1, y_list1 = trapezoidal.trapezoidal(func_f1, -2.0, 2.0, dx=1e-4)
trapezoidal.visualization(func_f1, area1, x_list1, y_list1)
print()
# sinc関数
def func_f2(x):
return np.sin(x)/x
area2, x_list2, y_list2 = trapezoidal.trapezoidal(func_f2, 0.0, 2.0*np.pi)
trapezoidal.visualization(func_f2, area2, x_list2, y_list2)
print()
注意すべきと思う点
微小区間の長さを小さくしすぎると誤差が大きくなる
普通の手計算の感覚で言うと、微小区間の長さが短いほど精度が上がる気がしますが、数値計算において絶対値が小さすぎる値を使う時は要注意です。今回の場合、非常に小さい数字を膨大な回数足し合わせる処理になるので、いわゆる丸め誤差が累積して結果がずれていきます。計算機は実は、正確な足し算が苦手なのです。例えば、「単精度実数で0.01を10000回足すと、結果が100.003になる」という話があります。倍精度ではどうなるかなど、興味ある方は色々試してみてください。
「0.01を10000回足すと100.003になる」問題でPythonの場合。double型がデフォなので普通の状態でもマシだけど、decimalモジュールを使うとより正確。 pic.twitter.com/9Mh32pKanc
— サンセット (@Sunset_Yuhi) November 18, 2018
関数の性質は確かめた方がいい
例えば$y = \frac{\sin(x)}{x}$の場合、解析的には$x=0$の点で連続かつ微分可能のはずですが、単純に$\frac{\sin(0)}{0}$を求めようとするとゼロ除算になってしまいます。この場合だけでなく、分母に変数を含んでいる場合には、積分可能な場合でも上手く数値積分できない可能性があります。また、関数の未定義点や不連続点がある場合にも、上手く計算ができません。可能ならば、関数の形を確認しておくといいと思います。
関数を限定すれば無限積分も計算できる
正規分布のような関数であれば、「微小区間の定積分値が一定値以下ならば終了」という条件を付けることで(delta_area<=1e-10とか)、無限積分も一応計算できます。ただし、三角関数のように$y=0$の線を何度も横切るような関数だと、途中で非常に小さい面積が計算されて止まってしまったりします。上手くやればなんとかなりそうですが、汎用性が無いコードしか思いつかなかったのでコードにはあまり反映しませんでした。
自作プログラムは使えるのか
SciPyには数値積分を行える機能があり、これはFortranの積分計算ライブラリQUADPACKを使っているそうです。精度のいい解を早く得られますし、特殊関数も扱えるとのことで、今回の自作プログラムを使うメリットはあまり無いかもしれません。下に実装例を書いていますが、これだけで積分値と推定誤差を出してくれます。
import numpy as np #NumPyライブラリ
from scipy import integrate
def func_f1(x):
return 3.0*x**2.0
result1 = integrate.quad(func_f1, -1.0, 1.0)
print(result1)
def func_f2(x):
return np.sin(x)/x
result2 = integrate.quad(func_f2, 0.0, 2.0*np.pi)
print(result2)