『クラウド量子計算入門』の演習を行う (4 位相シフトゲートの量子実験) その２

はじめに

こちらの本を読みつつ、演習・実験を試してみます。

• 『クラウド量子計算入門―IBMの量子シミュレーションと量子コンピュータ』

4 位相シフトゲートの量子実験

4.1 位相シフト演算とは

4.1.4 位相シフト演算 T でのアダマール変換

演習 4-6

量子シミュレータで、$ H|0\rangle $、$ T^{\dagger}H|0\rangle $、$ HT^{\dagger}H|0\rangle $ を確かめる量子回路を作成し、どのように量子ビットが回転するか行列計算とともに比較して確かめよ。

行列計算

H|0\rangle
=
\frac{1}{ \sqrt{2} }
\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}
\begin{bmatrix} 1 \\ 0 \end{bmatrix}
=
\frac{1}{ \sqrt{2} }
\begin{bmatrix} 1 \\ 1 \end{bmatrix}
=
\frac{ |0\rangle + |1\rangle }{ \sqrt{2} }

T^\dagger H|0\rangle
=
\frac{1}{ \sqrt{2} }
\begin{bmatrix} 1 & 0 \\ 0 & e^{-i(\pi/4)} \end{bmatrix}
\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}
\begin{bmatrix} 1 \\ 0 \end{bmatrix}
=
\frac{1}{ \sqrt{2} }
\begin{bmatrix} 1 \\ e^{-i(\pi/4)} \end{bmatrix}
=
\frac{ |0\rangle + e^{-i(\pi/4)} |1\rangle }{ \sqrt{2} }

測定

量子回路

ブロッホ球

c1[0]	n
0	4094
1	4098

c1[0]	n
0	4094
1	4098

c1[0]	n
0	7003
1	1189

演習 4-7

量子シミュレータで、$ H|1\rangle $、$ TH|1\rangle $、$ HTH|1\rangle $ を確かめる量子回路を作成し、どのように量子ビットが回転するか行列計算とともに比較して確かめよ。

行列計算

H|1\rangle
=
\frac{1}{ \sqrt{2} }
\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}
\begin{bmatrix} 0 \\ 1 \end{bmatrix}
=
\frac{1}{ \sqrt{2} }
\begin{bmatrix} 1 \\ -1 \end{bmatrix}
=
\frac{ |0\rangle - |1\rangle }{ \sqrt{2} }

T^\dagger H|1\rangle
=
\frac{1}{ \sqrt{2} }
\begin{bmatrix} 1 & 0 \\ 0 & e^{-i(\pi/4)} \end{bmatrix}
\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}
\begin{bmatrix} 0 \\ 1 \end{bmatrix}
=
\frac{1}{ \sqrt{2} }
\begin{bmatrix} 1 \\ -e^{-i(\pi/4)} \end{bmatrix}
=
\frac{ |0\rangle - e^{-i(\pi/4)} |1\rangle }{ \sqrt{2} }

HT^\dagger H|1\rangle
=
\frac{1}{ \sqrt{2} }
\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}
\frac{1}{ \sqrt{2} }
\begin{bmatrix} 1 & 0 \\ 0 & e^{-i(\pi/4)} \end{bmatrix}
\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}
\begin{bmatrix} 0 \\ 1 \end{bmatrix}
=
\frac{1}{2}
\begin{bmatrix} 1 - e^{-i(\pi/4)} \\ 1 + e^{-i(\pi/4)} \end{bmatrix}
=
\frac{ (1 - e^{-i(\pi/4)})|0\rangle + (1 + e^{-i(\pi/4)})|1\rangle }{2}

測定

量子回路

ブロッホ球

c1[0]	n
0	4094
1	4098

c1[0]	n
0	4094
1	4098

c1[0]	n
0	1172
1	7020

演習 4-8

量子シミュレータで、$ H|1\rangle $、$ T^{\dagger}H|1\rangle $、$ HT^{\dagger}H|1\rangle $ を確かめる量子回路を作成し、どのように量子ビットが回転するか行列計算とともに比較して確かめよ。

行列計算

H|1\rangle
=
\frac{1}{ \sqrt{2} }
\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}
\begin{bmatrix} 0 \\ 1 \end{bmatrix}
=
\frac{1}{ \sqrt{2} }
\begin{bmatrix} 1 \\ -1 \end{bmatrix}
=
\frac{ |0\rangle - |1\rangle }{ \sqrt{2} }

TH|1\rangle
=
\frac{1}{ \sqrt{2} }
\begin{bmatrix} 1 & 0 \\ 0 & e^{i(\pi/4)} \end{bmatrix}
\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}
\begin{bmatrix} 0 \\ 1 \end{bmatrix}
=
\frac{1}{ \sqrt{2} }
\begin{bmatrix} 1 & 0 \\ 0 & e^{i(\pi/4)} \end{bmatrix}
\begin{bmatrix} 1 \\ -1 \end{bmatrix}
=
\frac{ |0\rangle - e^{i(\pi/4)} |1\rangle }{ \sqrt{2} }

HTH|1\rangle
=
\frac{1}{ \sqrt{2} }
\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}
\frac{1}{ \sqrt{2} }
\begin{bmatrix} 1 & 0 \\ 0 & e^{i(\pi/4)} \end{bmatrix}
\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}
\begin{bmatrix} 0 \\ 1 \end{bmatrix}
=
\frac{1}{2}
\begin{bmatrix} 1 - e^{i(\pi/4)} \\ 1 + e^{i(\pi/4)} \end{bmatrix}
=
\frac{ (1 - e^{i(\pi/4)})|0\rangle + (1 + e^{i(\pi/4)})|1\rangle }{2}

測定

量子回路

ブロッホ球

c1[0]	n
0	4094
1	4098

c1[0]	n
0	1172
1	7020

演習 4-9

量子シミュレータで、初期状態 $ |1\rangle $ に対してアダマール演算 H と位相シフト演算 T との組み合わせを連続で作用させるとどうなるか、$ H|1\rangle $、$ TH|1\rangle $、$ HTH|1\rangle $、$ THTH|1\rangle $ として量子回路を作成して行列計算とともに比較して確かめよ。

行列計算

THTH|1\rangle
=
\begin{bmatrix} 1 & 0 \\ 0 & e^{i(\pi/4)} \end{bmatrix}
\frac{1}{ \sqrt{2} }
\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}
\begin{bmatrix} 1 & 0 \\ 0 & e^{i(\pi/4)} \end{bmatrix}
\frac{1}{ \sqrt{2} }
\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}
\begin{bmatrix} 0 \\ 1 \end{bmatrix}
=
\frac{1}{2}
\begin{bmatrix} 1 & 0 \\ 0 & e^{i(\pi/4)} \end{bmatrix}
\begin{bmatrix} 1 - e^{i(\pi/4)} \\ 1 + e^{i(\pi/4)} \end{bmatrix}
=
\frac{ (1 - e^{i(\pi/4)})|0\rangle + (e^{i(\pi/4)} + i)|1\rangle }{ \sqrt{2} }

測定

量子回路

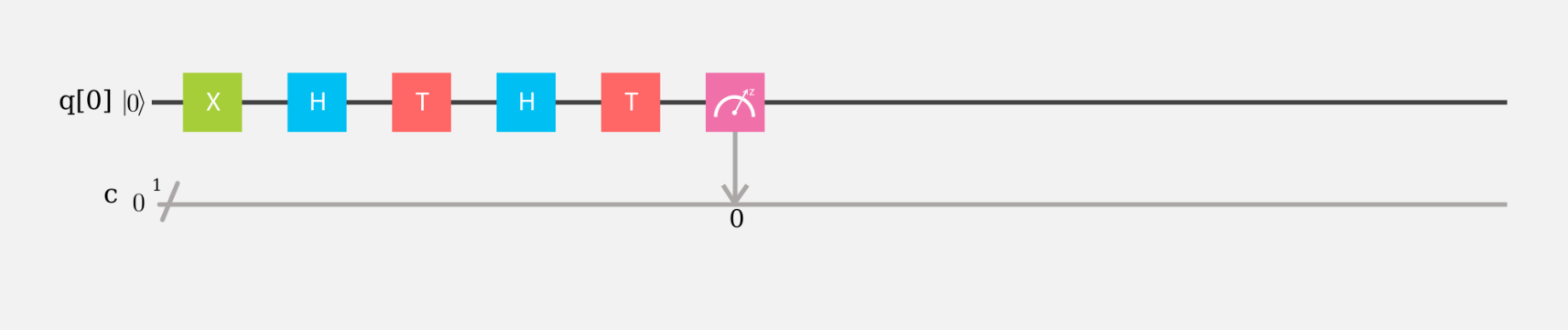
ブロッホ球

c1[0]	n
0	1172
1	7020