『クラウド量子計算入門』の演習を行う (5 制御 NOT ゲートの量子実験) その１

はじめに

こちらの本を読みつつ、演習・実験を試してみます。

• 『クラウド量子計算入門―IBMの量子シミュレーションと量子コンピュータ』

以下、過去分です。

• 「クラウド量子計算入門に関するN件の投稿 - Qiita」

---

5 制御 NOT ゲートの量子実験

5.2 制御 NOT ゲートによるもつれ状態生成

5.2.1 ベル状態の生成

演習 5-1

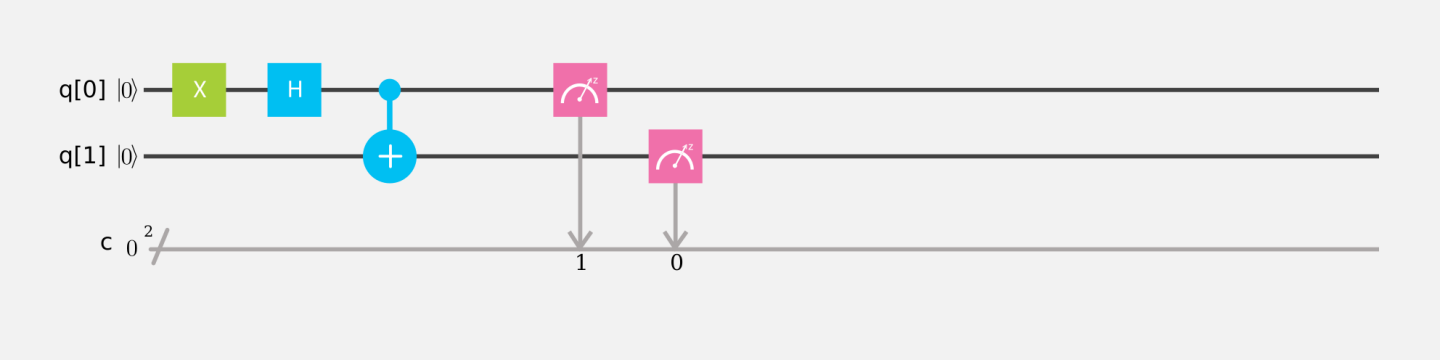
量子シミュレータで、次のように初期状態 $ |10\rangle $ でアダマール演算と制御 NOT ゲートとを用いて、もつれ状態を生成する量子回路を作成し、実行結果が行列計算とも一致しているか確かめよ。

|10\rangle
\rightarrow^{H \otimes I}
\rightarrow^{CNOT}
\frac{1}{ \sqrt{2} } ( |00\rangle - |11\rangle )

行列計算

H \otimes I |10\rangle
=
\frac{1}{ \sqrt{2} }
\begin{bmatrix}
1
\begin{bmatrix}
1 & 0 \\
0 & 1
\end{bmatrix} &
1
\begin{bmatrix}
1 & 0 \\
0 & 1
\end{bmatrix} \\
1
\begin{bmatrix}
1 & 0 \\
0 & 1
\end{bmatrix} &
-1
\begin{bmatrix}
1 & 0 \\
0 & 1
\end{bmatrix}
\end{bmatrix}
\begin{bmatrix}
0 \\
0 \\
1 \\
0
\end{bmatrix}
=
\frac{1}{ \sqrt{2} }
\begin{bmatrix}
1 \\
0 \\
-1 \\
0
\end{bmatrix}
=
\frac{1}{ \sqrt{2} }(|00\rangle - |10\rangle) \\

\rightarrow^{CNOT} 
\frac{1}{ \sqrt{2} }(|00\rangle - |11\rangle)

量子回路

測定

c[2]	n
00	4076
11	4116

演習 5-2

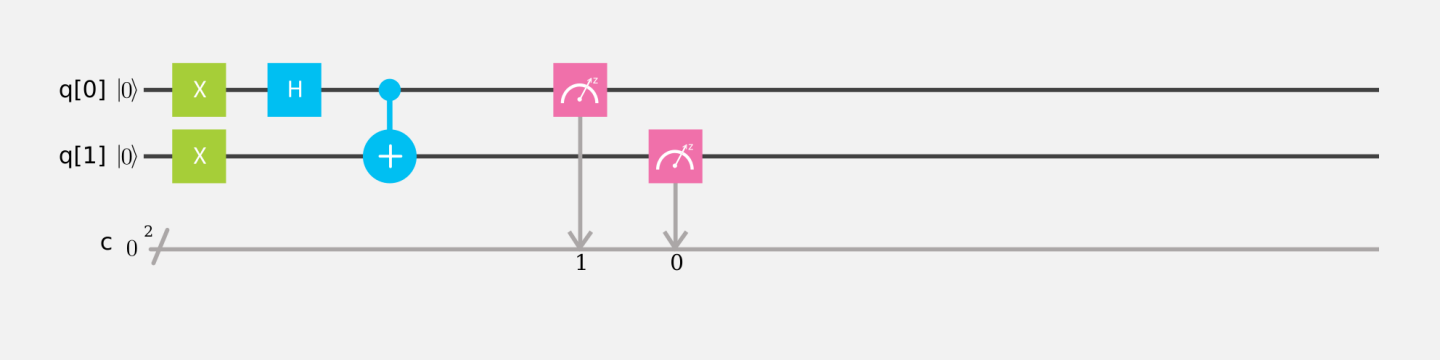
量子シミュレータで、次のように初期状態 $ |01\rangle $ でアダマール演算と制御 NOT ゲートとを用いて、もつれ状態を生成する量子回路を作成し、実行結果が行列計算とも一致しているか確かめよ。

|11\rangle
\rightarrow^{H \otimes I}
\rightarrow^{CNOT}
\frac{1}{ \sqrt{2} } ( |01\rangle - |10\rangle )

量子回路

測定

c[2]	n
01	4076
10	4116

5.2.2 制御 NOT ゲートの上下反転

演習 5-3

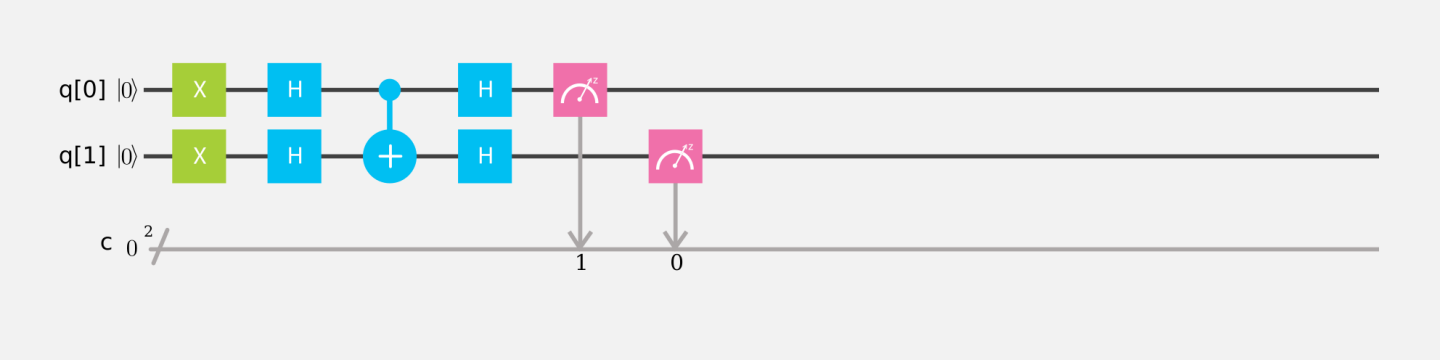
量子シミュレータで、制御 NOT ゲートの前後に制御ゲートも目標ゲートもアダマール変換で挟んだ量子回路を作成し、入力ビット $ |11\rangle $ とすると、その実行結果とベクトル計算式とで一致しているか確かめよ。

ベクトル計算

|11\rangle \rightarrow^{H \otimes H}
=
\frac{ |0\rangle - |1\rangle }{ \sqrt{2} }
\otimes
\frac{ |0\rangle - |1\rangle }{ \sqrt{2} }
=
\frac{1}{ \sqrt{2} }( |00\rangle - |01\rangle - |10\rangle + |11\rangle )

\rightarrow^{CNOT}
\frac{1}{ \sqrt{2} }( |00\rangle - |01\rangle + |10\rangle - |11\rangle )
=
\frac{ |0\rangle + |1\rangle }{ \sqrt{2} }
\otimes
\frac{ |0\rangle - |1\rangle }{ \sqrt{2} }
\rightarrow^{H \otimes H}
|01\rangle

量子回路

測定

c[2]	n
01	8192