Numpyを使った線形回帰の方法

はじめに

この記事は筆者がhttps://www.udemy.com/share/1013lqB0AedFdUR34=/
にて学んだことの復習を目的としています

書くこと

• 最小二乗法の軽い導出
• pandasのDataFrameからnumpyのarrayに変換して計算してみる

最小二乗法の導出

あるデータセット[x, y]が与えられてるとします。
xは説明変数でyは目的変数。例えば、身長が増えれば体重が増えるのでこの場合x=身長、y=体重となる。

そして与えられたデータxからyを予測したい。そのときの予測値を$\hat{y}$とし、以下のような関係式と仮定する。

\hat{y} = ax + b

ここで$\hat{y}$を正解値$y$に限りなく近づけることが目標になる。よって

Error = y - \hat{y} = y - ax + b =0

となるa,bを探すことが大切になる。
これ以降の説明は以下のリンクから見てください。
http://arduinopid.web.fc2.com/P7.html

numpyを用いた線形回帰

まずモジュールのインポート

import pandas as pd
from pandas import Series, DataFrame
import numpy as np

import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('whitegrid')
%matplotlib inline

あと今回用いるデータセットをダウンロードする

from sklearn.datasets import load_boston

boston = load_boston()

今回はこのデータフレーム内のRM(average number of rooms per dwelling)とtarget(Price)を使います。本来はsns.pairplotやsns.jointplotなどを用いて線形回帰（比例）の関係がありそうな変数を探しますが、今回はあらかじめこの二つの変数には比例関係があるとします。

boston_df = DataFrame(boston.data)
# 列名をつける
boston_df.columns = boston.feature_names
# targetじゃわかりづらいので新たに列をコピー
boston_df['Price'] = boston.target
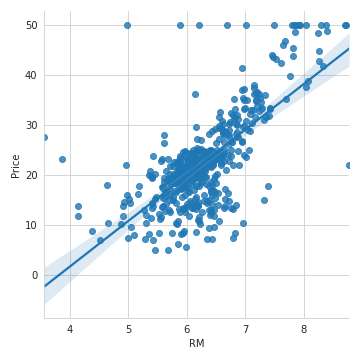
# 散布図と回帰直線の表示
sns.lmplot('RM', 'Price', data=boston_df)

この回帰直線を計算で出そう。
使うのはnp.linalg.lstsq(X, Y)。
ただ、このXには特定の形を持ったアレイが必要なのでそのために成形する。

X = boston_df.RM
Y = boston_df.Price
# [x,1]の形にする
X = np.array([ [value[0], 1] for value in X])
# 浮動小数点の型に変換
X = X.astype(np.float64)
# a, bにそれぞれの予測値が格納される
a, b = np.linalg.lstsq(X, Y)[0]

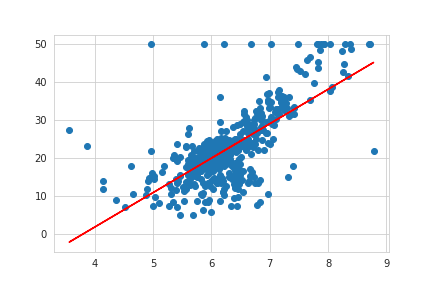
これで計算は終わり。結果を見てみよう

plt.plot(boston_df.RM, boston_df.Price, 'o')
x = boston_df.RM
plt.plot(x, a*x+b, 'r')

np.linalg.lstsqについて補足

公式ドキュメントはこちら
https://numpy.org/doc/stable/reference/generated/numpy.linalg.lstsq.html#numpy.linalg.lstsq

numpy.linalg.lstsq(a, b, rcond='warn')

• パラメータ
  -- 係数行列a（M, N）、独立変数b（M,）or （M, K）、rcond
• 戻り値
  -- 最小二乗解p, 残差の合計residues, 係数行列aのランクrank, aのsingular value

np.linalg.lstsq(X, Y)[1]とすれば残差の合計も取り出せる