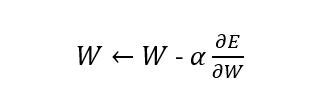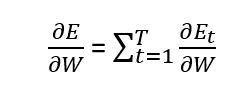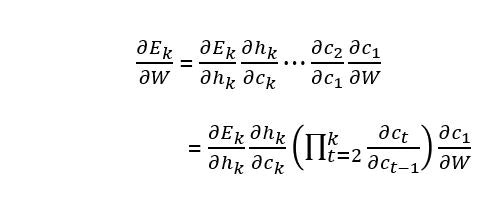はじめに
この記事はRNN初学者によって書かれています。初心者目線の分かりやすい説明にはなりますが、解釈に語弊がある可能性があります。
RNNとLSTMについて簡単に
RNN
RNNとは時系列データ(前の結果によって次の結果が左右されるもの。例:株価、音、言語)に用いられる機械学習の一つ。Recurrent Neural Networkの略で日本語訳で再起型ネットワークという。
余談だが機械学習という枠組みの中に深層学習(ディープラーニング)というカテゴリがあり、RNNはここにカテゴライズされる。他には畳み込みニューラルネットワークのCNNなどがある。
LSTM
先に結論を言うとRNNは問題がある。それは時系列データが多くなればなるほど有効性がなくなることだ。もう少し具体的にいうとディープラーニングはバックプロパゲーション(誤差逆伝播法)というアルゴリズムで学習を進めていくのだが、RNNはそのバックプロパゲーションの中で値がどんどん小さくなってしまう(→0)。
簡単なイメージとして、再帰型というのはプログラミングでいうとfor文にあたる。RNNはforループの中で1以下の数字を掛け算し続けているといった感じ。
input = 10
N = 100
for i in N:
input *= 0.1 #1以下
print(input)
>>>0.0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001
この0に限りなくなってしまう問題を勾配消失という。筆者はまだ理解してないがこの逆の勾配爆発もありえるらしい。多分これの逆パターンだろう。
とにかくこの勾配消失問題をクリア、つまり0にならないようにしたのがLSTMという方法だ。
RNNの勾配消失を詳しく
RNNの勾配消失を理解するにはバックプロパゲーション(誤差逆伝播)を理解している必要がある。知らない人のため軽く説明だけします。いらない人は飛ばしてください。
誤差逆伝播
深層学習のほとんどはニューラルネットワークという脳の神経を模した構造です。
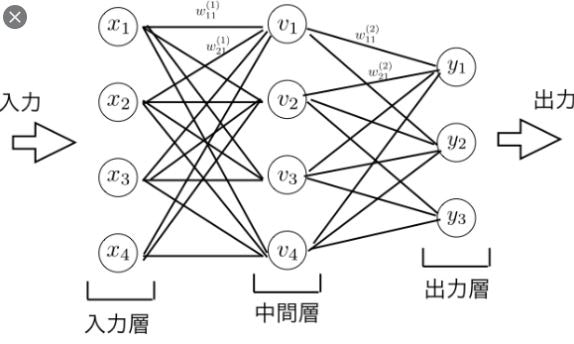
$v_1$ = $f(w_{11}x_1 + w_{21}x_2 + \cdots + w_{41}x_4 + b_{v_1}) (1)$
となります。
この$w$は重み,$b$はバイアスといい、$y=ax+b$でいう傾きaと切片bにあたります。この式を活性化関数という関数に代入します。この活性化関数はデータによって使い分けたりするものです。$f(x) = x$ や $f(x) = \frac{1}{1 + e^{-x}}$などがあります。
まず初めに適当な初期値をすべてのwとbに与えます。そして元となる入力データの$x_1~x_4$があります。すると式(1)の要領で$v_1$~$v_4$が求まり、$y_1$~$y_3$も$v_1$~$v_4$の求め方と同じくwとbとf(x)により、$y_1$~$y_3$が求まります。
この$y_1$~$y_3$が予測値になります。この場合答えが3種類あるデータの予測をしていることになります。
さて予測値$y_1$~$y_3$に対して、正解があらかじめ用意されています。逆に言うと正解がないとできません。ニューラルネットワークは教師あり学習です。
正解を$t_1$~$t_3$としましょう。さて予測値を正解に近づけるのが目標ですよね。では両者の差を最小化すればいいですね。
$argmin(y_1-t_1)$
また正解が複数あるのでそれぞれ4つの差の合計を最小化すればよさそうです。
$argmin[(y_1-t_1) \cdots + (y_3-t_3)]$
いや実はこれだめです。片方の差がマイナスで他の差がプラスとかだと差を打ち消しあってしまう。では差の絶対値、または2乗にしましょう。
$lossfunc(二乗和誤差) = argmin[(y_1-t_1)^2 \cdots + (y_3-t_3)^2]$
$lossfunc(絶対値誤差) = argmin[|y_1-t_1| \cdots + |y_3-t_3|]$
これが完成形です。このように正解データと予測データの差を最小化することを目指すのがニューラルネットワークです。またこの差を評価する式を損失関数といいます。この式も場合や目的により変わります。
さて、実際にどうやって差を小さくするのでしょうか?
では仮に$lossfunc = x^2$のとき最小値をどうやって見つけますか?高校数学を習った人なら分かりますね。$\frac{d(lossfunc)}{dx} = 0$となる点xを探しますよね。
そう、つまり
予測値を正解に近づける=損失関数を最小化する=損失関数の微分を0に近づける
ということになります。
さて上のモデルを見返してほしいのですが、私たちがいじることができるのはwとbだけになります。この最初適当に決めたwとbを最適化します。
損失関数に含まれている$y_1$~$y_3$は(1)から$v_1$~$v_4$と${w_{11}}^{(2)}$~${w_{41}}^{(2)}$と$b_{y_1}$~$b_{y_3}$で表されますね。(式(1)のvとxをyとvに置き換えればそうなる)
$lossfunc(y,t)=lossfunc(v,w,b,t)$
となるわけです。
さて
例えば、
$\frac{d(lossfunc)}{d{w_{11}}^{(2)}} = 0$
となる${w_{11}}^{(2)}$を見つけたら${w_{11}}^{(2)}$は最適化されたことになりますね。
これを各パラメータごとに行えばいいのです。
$\frac{d(lossfunc)}{d{w_{21}}^{(2)}} = 0 \hspace{15pt} \frac{d(lossfunc)}{b_{y_1}} = 0$
$\frac{d(lossfunc)}{d{w_{31}}^{(2)}} = 0 \hspace{15pt} \frac{d(lossfunc)}{b_{y_2}} = 0$
$\frac{d(lossfunc)}{d{w_{41}}^{(2)}} = 0 \hspace{15pt} \frac{d(lossfunc)}{b_{y_3}} = 0$
PCの計算上この微分=0への近づけ方は以下のようになります。
$w_{11} = w_{11} - \alpha\frac{d(lossfunc)}{d{w_{11}}^{(2)}}$
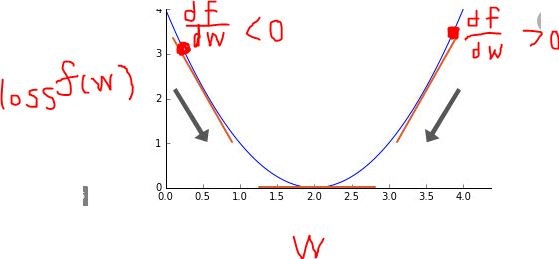
$\alpha$はどのくらい1回の更新を反映させるか決める定数で1~0の値をとります。この式の理解として、$\frac{d(lossfunc)}{d{w_{11}}^{(2)}}$がプラスであれば最小値はマイナスのほうに、マイナスであれば最小値はプラスのほうにあることになるので以下の図よ矢印のような操作をしているわけです。
長くなりましたが誤差逆伝播の説明はここまでです。
$w_{11} = w_{11} - \alpha\frac{d(lossfunc)}{d{w_{11}}^{(2)}}$
誤差逆伝播ではこの式を行っているんだよと知っておけばいいです。
という結論をもとにRNNの勾配消失やLSTMの説明をします。
ここを飛ばさずに読んだ人は上のRNNとLSTMについてから読み直したら理解しやすいかも。
RNNの勾配消失
ここからの説明はこのサイトをなぞったものになります。画像も流用させていただきます。TOEIC600くらいあれば読めると思います。
https://medium.com/datadriveninvestor/how-do-lstm-networks-solve-the-problem-of-vanishing-gradients-a6784971a577
では本題です。
誤差逆伝播法を理解していれば理屈は簡単です。まずRNNの構造は以下のようになっています。
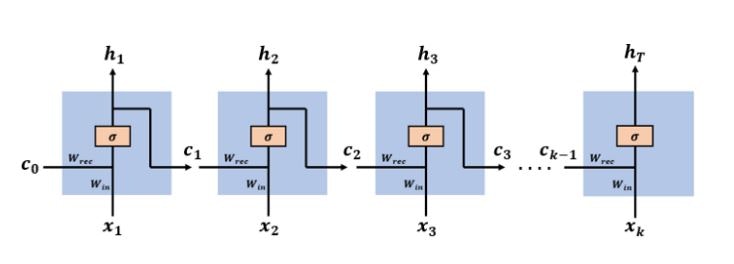
$x_1$~$x_k$が時系列データ(入力)になります。$h_1$~$h_r$が出力です。またこの出力が次の学習の入力$c_2$~$c_{k-1}$となります。σは活性化関数のシグモイド関数を意味していて
$\sigma(x) = \frac{1}{1 + e^{-x}}$
となります。ニューラルネットワークと同じようにある時点の出力$h_t$は
$ h_t = \sigma(w_{rec} c_{t-1} + w_{in}x_t)$
前の時刻の出力$c_{t-1}$と本時刻の入力$x_t$に重みをかけ、足し合わせたものを活性化関数に入れています。
時刻tの時の正解データ$t_t$と出力$h_t$の差の絶対値を$E_t$とします。誤差逆伝播はこの差を最小化するのでしたね。例として$w_{rec}$の勾配を見てみましょう。
$\frac{dE}{dw_{rec}} = \sum_{t=0}^{k} \frac{dE_t}{dw_{rec}}$
と定義されます(全損失は各損失の和となっている)。したがって
$w_{rec} = w_{rec} - \alpha\frac{dE}{dw_{rec}} =w_{rec} - \alpha \sum_{t=0}^{k} \frac{dE_t}{dw_{rec}}$
という誤差逆伝播を行います。($w_{in}$の時も同様。)
さてRNNはデータ数が多いと勾配消失してしまうといいました。それは上式の2項目が働かない、つまり
$\lim_{k\to \infty} \sum_{t=1}^{k} \frac{dE_t}{dw_{rec}} = 0$
となってしまい重みの更新ができていないということなのです。
解説するため、連鎖律を用いて次のように変形します。(重みは以降Wにし、$E_k$は時刻kのときの誤差)
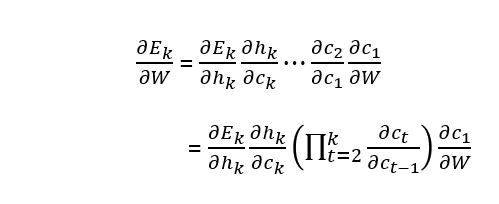
kが多いと$\prod_{t=2}^k \frac{\partial c_t}{\partial c_{t-1}}$はたくさんの掛け算をすることが分かります。
$c_t$はRNNの構造の説明時に求めました。
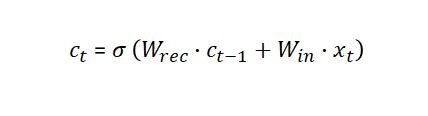
でしたね。なので
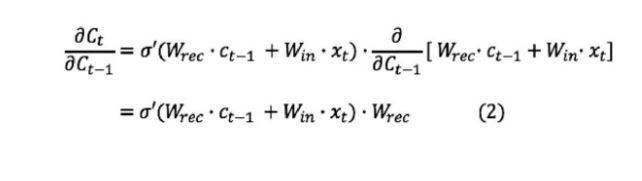
上式からk(学習回数)が多いと$\frac{\partial c_t}{\partial c_{t-1}}$が多く掛け算される=$\sigma'$が多く掛け算されることがわかります。
ここまでわかればもう少しです。$\sigma'$がポイントです。シグモイド関数はハイパボリックタンジェントの形に変形できます。
$\sigma(x) = \frac{1}{1 + e^{-x}} =\frac{1}{2}(1 + tanh(\frac{1}{2}ax))$
なので
$\sigma'(x)= \frac{1}{2}tanh'(\frac{1}{2}ax)=\frac{a}{4}\frac{1}{{cosh}^2 x}$
となります。
そしてtanhの微分は必ず1以下0以上の値をとります。これに$\frac{a}{4}(<1)$がかかるのでより小さくなりますね。
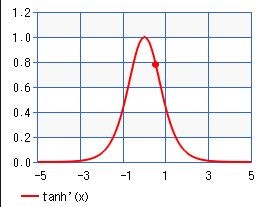
そろそろ見えてきましたね。冒頭に述べた通りRNNは誤差逆伝播中に1以下の数字を再帰的にかけ続けているのです。なのでデータ数kが増えればかける回数が増えるので勾配消失が起こります。
$\sigma(x)'= {tanh(\frac{1}{2}ax)}' <=1$
LSTM
近日作成予定