はじめに
この記事は統計検定準1級および1級合格に向けて作成されたものです。下の参考書の第一章に当たります。
この記事では ベイズの定理および包除原理およびその他の公式についてまとめます。
ベイズの定理
まず条件付き確率についての公式について
$$P(A|B)P(B) = P(B|A)P(A)=P(A\cap B) \tag{1}$$
式(1)の理解
この公式はベン図を用いて考えるとわかりやすいです。
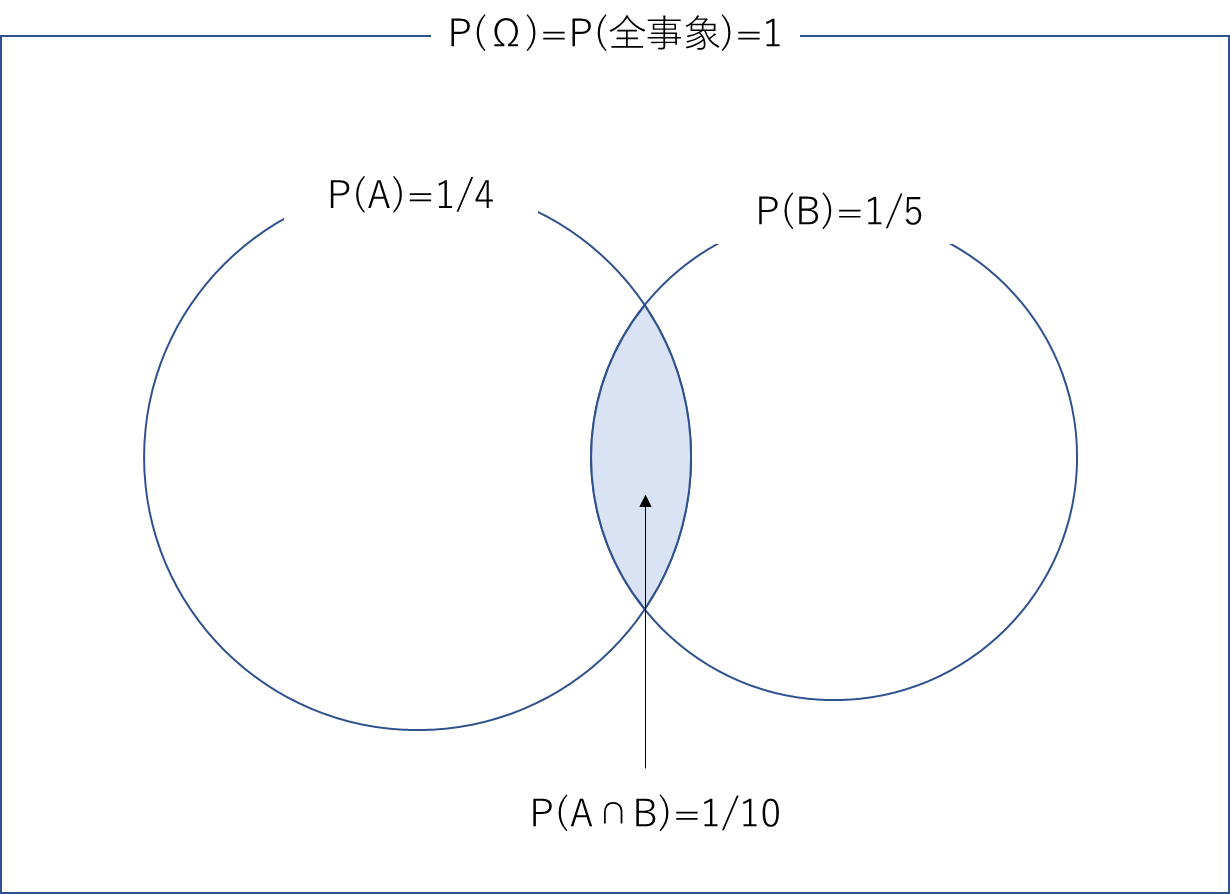
$A\cap B$ :AでありかつBである事象なのでそれぞれの共通部分となります。
$A|B$ :BのもとでAである事象、つまり$P(A|B)$とはBに当たる円面積のうちAと重なる部分の占める面積の割合を意味します。なので$P(A|B)$に事象Bの得られる確率$P(B)$を掛け合わせます。
具体例 :P(大学に進学する人|日本人)は高く、0.8。しかしこれは日本人かつ大学に進学する人が世界人口の80%を占める($P(進学\cap 日本人)=0.8$)とはもちろん言えない。なぜなら0.8とは日本人口のうち8割が進学するという意味であり、P(日本人)=1.3億人/79億人=0.016を考慮していないから。なので全世界人口における日本人かつ大学に進学する人の割合は$P(大学に進学する人|日本人)P(日本人)=0.8 \times 0.016$が正しい。
以上から式(1)が得られます。
$P(A|B)P(B) = P(B|A)P(A)=P(A\cap B)$をさらに変形すればベイズの定理の完成です。
$$P(B|A)= \frac{P(A|B)P(B)}{P(A)}=\frac{P(A|B)P(B)}{P(A|B)P(B)+P(A|B^c)P(B^c)} \tag{2}$$
式(2)の理解
等号1つ目はただの移項です。等号2つ目では
$$P(A)=P(A|B)P(B)+P(A|B^c)P(B^c)$$
を用いて変形しています。
これもベン図を用いるとわかりやすいです。
右辺第一項はAとBの共通部分$A\cap B$の確率となります。右辺第二項についてベン図で示すとまず$P(B^c)$とはB以外の事象が得られる確率であり

これを踏まえると$P(A|B^c)$とは$B^c$のうちAが占める部分を示すので
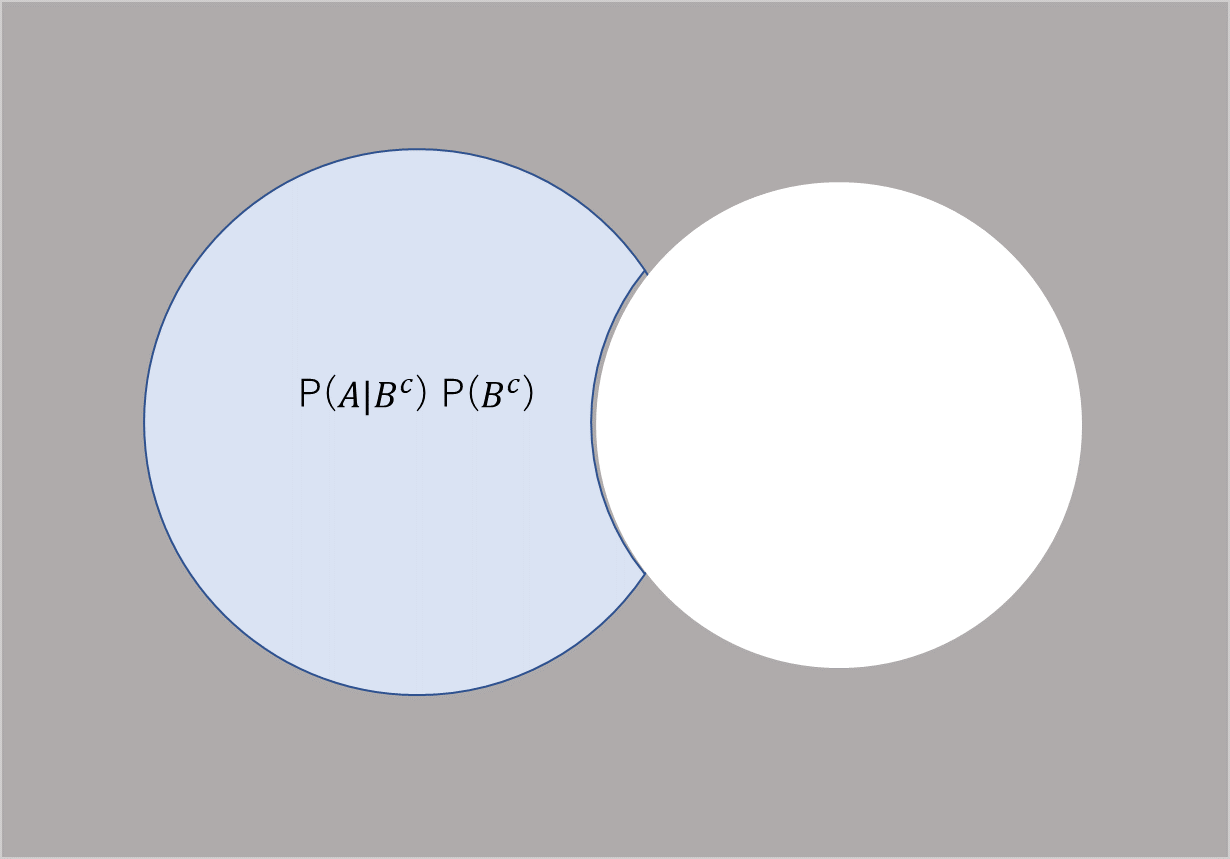
よってこれら二つを足すと$P(A)$と一致します。したがって式(2)が得られます。
では例題として次を解いてください。
例題1
P(A)=1/4, P(B)=1/5, P($A\cap B$)=1/10 のときP(A|B)およびP(B|A)を求めよ。
包除原理
和事象$A \cup B$と積事象$A\cap B$を結びつける公式です。
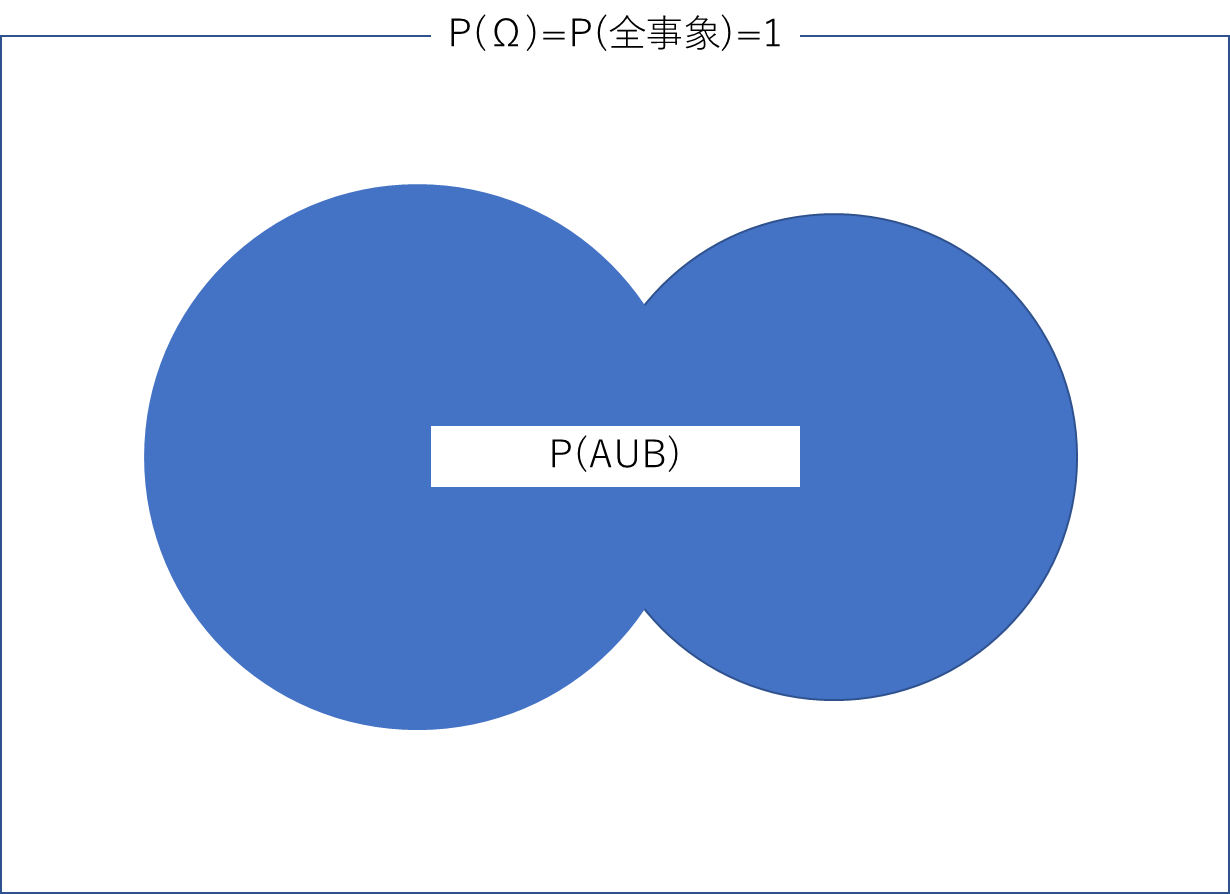
$$P(A \cup B)=P(A)+P(B) - P(A \cap B) \tag{3}$$
これはベン図を用いて考えればすぐわかります。$A\cup B$はAまたはBである事象を意味します。
では事象3つを切り取って$P(A\cup B \cup C)$はどのように表されるでしょう。ベン図を用いて直感的に解くのは大変ですがなんとか可能でしょう。
$$ P(A\cup B \cup C)=P(A)+P(B)+P(C)-P(A\cap B)-P(A\cap C)-P(B\cap C) + P(A \cap B \cap C ) \tag{4}$$
これが4事象の場合のベン図となってはもうベン図を用いて導出するのは無理でしょう。
しかし2事象、3事象の結果に規則性があります。
奇数個の事象に関する確率は足し算、偶数個の事象に関する確率は引き算すればいいのです。
この規則性を知っていればn個の事象の和の確率$P(X_1 \cup \dots \cup X_n)$についての公式も求まります。
ただ、統計検定に出題されるのはせいぜい3事象だと思われます。
例題2
4事象の和の確率についての包除原理を書け
包除原理とベイズの定理の組み合わせ
式(2)および式(3)を組み合わせた問題はよく検定に出題されます。これらが組み合わさるだけで一見すると手がつかないような問題になります。
例題3
$P(A\cap B)=1/5,P(B|A)=1/2,P(A|B)=1/3$のとき$P(A\cup B)$を求めよ
また文章問題により確率が提示されているパターンよく出題されます。
さらに次の例題4の4.2は3事象のパターンなのでとても複雑です。
例題4
高齢者のうち100人に1人がある病気にかかっているとする。この病気には検査1と検査2がある。検査1は本当にその病気にかかっているとき99%で陽性反応を示すが、一方で病気でない場合でも2%の確率で陽性反応を出してしまう。検査2は検査1で陽性とは診断された人にのみ行う。検査2は本当にその病気にかかっている場合90%で陽性反応を示すが、一方で病気でない場合でも10%の確率で陽性反応を示す。
4.1 ある高齢者Aが検査1を受けたところ結果は陽性だった。Aが本当に病気である確率を求めよ。
4.2 Aは検査1で陽性だったため検査2に進んだ。その結果再度陽性と診断された。Aが本当に病気である確率を求めよ。
覚えるべき式のまとめ
$$P(A|B)P(B) = P(B|A)P(A)=P(A\cap B) \tag{1}$$
$$P(B|A)= \frac{P(A|B)P(B)}{P(A)}=\frac{P(A|B)P(B)}{P(A|B)P(B)+P(A|B^c)P(B^c)} \tag{2}$$
$$P(A \cup B)=P(A)+P(B) - P(A \cap B) \tag{3}$$
例題解答
$P(A|B)=P(A\cap B)/P(B)=\frac{1}{2}$, $P(B|A)=P(B\cap A)/P(A)=\frac{2}{5}$
$P(A\cup B \cup C \cup D) = P(A)+P(B)+P(C)+P(D) -P(A\cap B)-P(A\cap C)-P(A\cap D)-P(B\cap C)-P(B\cap D)-P(C\cap D) +P(A \cap B \cap C)+P(A\cap C \cap D)+P(A\cap B \cap D)+P(B\cap C\cap D) -P(A\cap B \cap C \cap D)$
$P(A\cup B)=P(A)+P(B) - P(A \cap B)=\frac{P(A \cap B)}{P(B|A)}+\frac{P(A \cap B)}{P(A|B)}-P(A\cap B) =\frac{P(A\cap B)}{P(A|B)P(B|A)}(P(A|B)+P(B|A)-P(A|B)P(B|A))=\frac{\frac{1}{5}}{\frac{1}{3}\frac{1}{2}}(\frac{1}{3}+\frac{1}{2}-\frac{1}{3}\frac{1}{2})=\frac{4}{5}$
$X_i\in{0,1}$: $X_i=1$なら検査iで陽性、$X_i=0$なら検査iで陰性、$Y\in{0,1}$: $Y=1$なら病気にかかっている、$Y=0$なら病気にかかっていないとする。
4.1
$P(Y=1|X_1=1)=\frac{P(X_1=1|Y=1)P(Y=1)}{P(X_1=1|Y=1)P(Y=1)+P(X_1=1|Y=0)P(Y=0)}=\frac{0.99\times 0.01}{0.99\times 0.01+0.02\times 0.99}=\frac{1}{3}$
4.2
$P(Y=1|X_1=1, X_2=1)=\frac{P(X_1=1,X_2=1|Y=1)P(Y=1)}{P(X_1=1,X_2=1)}$
また
$P(X_1=1,X_2=1)=P(X_2=1|X_1=1)P(X_1=1), $ $P(X_1=1,X_2=1|Y=1)P(Y=1)=P(X_2=1|X_1=1,Y=1)P(X_1=1|Y=1)P(Y=1)=P(X_2=1|X_1=1,Y=1)P(X_1=1,Y=1)$
より
$P(Y=1|X_1=1, X_2=1)=\frac{P(X_2=1|X_1=1,Y=1)P(Y=1|X_1=1)}{P(X_2=1|X_1=1)}$
ここで$P(X_2=1|X_1=1)=P(X_2=1|X_1=1, Y=1)P(Y=1|X_1=1)+P(X_2=1|X_1=1, Y=0)P(Y=0|X_1=1)=\frac{9}{10}\frac{1}{3}+\frac{1}{10}\frac{2}{3}=\frac{11}{30}$
よって
$P(Y=1|X_1=1, X_2=1)=\frac{P(X_2=1|X_1=1,Y=1)P(Y=1|X_1=1)}{P(X_2=1|X_1=1)}=\frac{\frac{9}{10}\frac{1}{3}}{\frac{11}{30}}=\frac{9}{11}$
補足:4.1と4.2の答えを比較すると検査をする前のAが病気である確率は1%,検査1で陽性という結果を受けて確率は33%に、さらに検査2で陽性という結果を受けて確率は82%にまで上昇している。一方厳密な値は示さないが、もし検査1が陰性であった場合は確率は1%を大きく下回る値になる。これは直感的に繰り返し陽性(陰性)と診断されればされるほど、より一層本当に病気にかかっている(いない)のだろうと考えるのと一致している。このようにベイズの定理とは結果を得たことにより事前の確率が更新されていくこととも捉えられる。この解釈はベイズ法や共役事前分布などに応用されている。
