重回帰分析2
なぜ,重回帰分析についての記事が何回も何回も掲載されるのか。それも,重回帰分析すらでなくて単回帰(直線回帰)分析。しかも,不十分な記事が。
重回帰分析の導出なんて,誰が何回やっても同じなんだから,それを個別に何回も何回も記述しても,意味ないじゃん。
その割には,注意すべき点についてちゃんと記述できている記事も少ないし。
重回帰分析は一筋縄ではいかない。数式だけ眺めていても,わからないことがたくさんある。
プラットフォームはいろいろあるが,R でやってみる(Python の人は書き換えてみてね)。
まずは,データフレームを作る。ただし,ある意図を持ったデータなので,注意深く分析することを心がけて欲しい。
library(MASS)
options(digits=16)
set.seed(1234567890)
nc = 20
r = matrix(c(
1.0, 0.6, 0.5, 0.1,
0.6, 1.0, 0.4, 0.7,
0.5, 0.4, 1.0, 0.6,
0.1, 0.7, 0.6, 1.0), ncol=4)
z <- mvrnorm(nc, mu=rep(0, 4), r, empirical=TRUE)
z = round(t(t(z)*c(3, 4, 5, 6) + c(50, 40, 30, 60)), 1)
df = data.frame(z)
colnames(df) = c("y", "x1", "x2", "x3")
head(df)
| y | x1 | x2 | x3 | |
|---|---|---|---|---|
| 1 | 45.4 | 38.3 | 27.7 | 63.5 |
| 2 | 50.4 | 44.0 | 37.1 | 66.7 |
| 3 | 48.1 | 39.2 | 31.8 | 61.8 |
| 4 | 47.9 | 31.3 | 24.1 | 46.9 |
| 5 | 49.2 | 40.4 | 32.4 | 67.6 |
| 6 | 49.1 | 43.1 | 29.7 | 65.1 |
相関係数を求めてみよう。実は,データフレームを作るときに指定した r に他ならない(データを作るときに丸めたのでちょっとだけ違う)
round(cor(df), 4)
| y | x1 | x2 | x3 | |
|---|---|---|---|---|
| y | 1.0000 | 0.5982 | 0.4994 | 0.0979 |
| x1 | 0.5982 | 1.0000 | 0.4017 | 0.7019 |
| x2 | 0.4994 | 0.4017 | 1.0000 | 0.5991 |
| x3 | 0.0979 | 0.7019 | 0.5991 | 1.0000 |
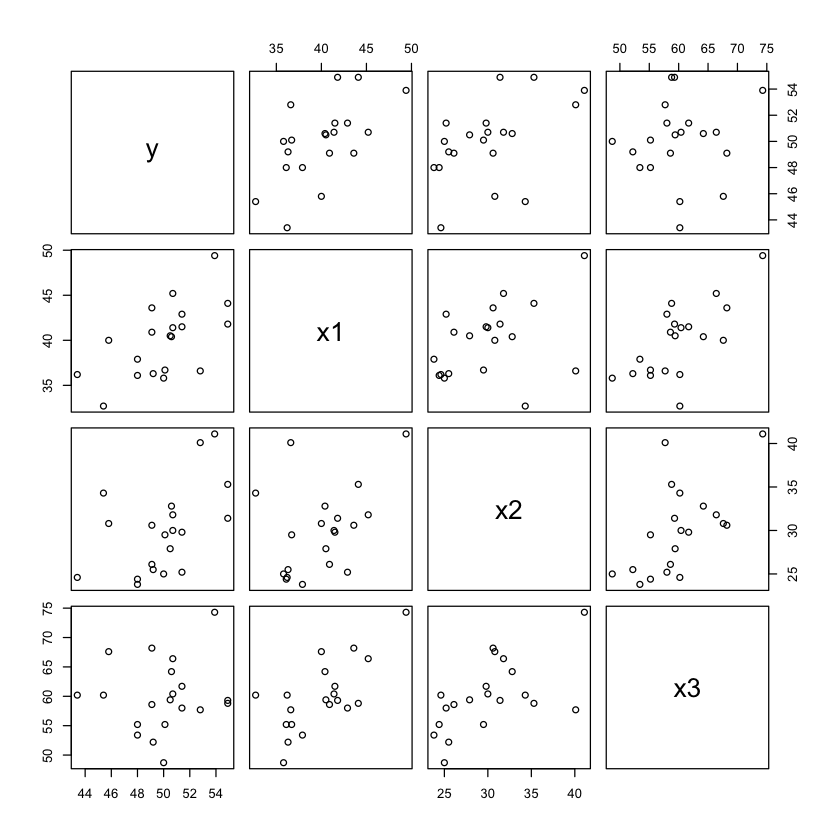
散布図を描いてみても,相関係数が 0.5 とか 0.7 くらいでも,あまりぱっとしない。
こんなので予測できるか?(機械学習の教育用データは,もっと相関の低い変数が一杯ある)
plot(df)
データについての所見
従属変数 y ともっとも相関の高いのは x1。次いで x2。x3 とはほとんど相関がないといえるレベルだ。
普通の人は,「重回帰分析するときに,x3 なんか使わないよね!」と思うかも知れない。
lm.ans1 = lm(y ~ x1 + x2, data=df)
summary(lm.ans1)
Call:
lm(formula = y ~ x1 + x2, data = df)
Residuals:
Min 1Q Median 3Q
-3.5656990721298 -1.8009686436998 -0.9731367460045 2.2515107463428
Max
3.1338362693141
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 30.1508994389561 5.6250775499563 5.36009 5.1956e-05 ***
x1 0.3566805720560 0.1493963265573 2.38748 0.028847 *
x2 0.1860625892935 0.1195547419975 1.55630 0.138057
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.387951045993 on 17 degrees of freedom
Multiple R-squared: 0.437902856506, Adjusted R-squared: 0.3717737808009
F-statistic: 6.62194128432 on 2 and 17 DF, p-value: 0.007471309290127
plot(df$y, predict(lm.ans1))
abline(0, 1, col="red")
どうですか,分析結果の解釈は。
決定係数 0.4379 とな。これじゃあ,重回帰分析は失敗だ。実測値と予測値の図を見てもわかる。
回帰の分散分析の p 値が 0.0074 であってもだ。
y との相関係数が 0.5 くらいもあった x2 すら,偏回帰係数の検定の p 値は 0.1381 で,偏回帰係数が 0 であるという帰無仮説を棄却できていない。
ところで,x3 も使ったらどうなると思う?(そもそも,使おうなんて思っていないだろうが)。
lm.ans2 = lm(y ~ x1 + x2 + x3, data=df)
summary(lm.ans2)
Call:
lm(formula = y ~ x1 + x2 + x3, data = df)
Residuals:
Min 1Q Median 3Q
-2.2483635860615 -0.4904258216178 -0.2910102631902 0.4773558776720
Max
1.9745355334776
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 37.45522309865842 2.67953807205067 13.97824 2.1903e-10 ***
x1 0.80518187920135 0.08640552755012 9.31864 7.2650e-08 ***
x2 0.43287512241041 0.06151436784887 7.03698 2.8081e-06 ***
x3 -0.54414586565041 0.06594139634562 -8.25196 3.7001e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.073655938906 on 16 degrees of freedom
Multiple R-squared: 0.8930546607771, Adjusted R-squared: 0.8730024096729
F-statistic: 44.53637928892 on 3 and 16 DF, p-value: 5.434308586e-08
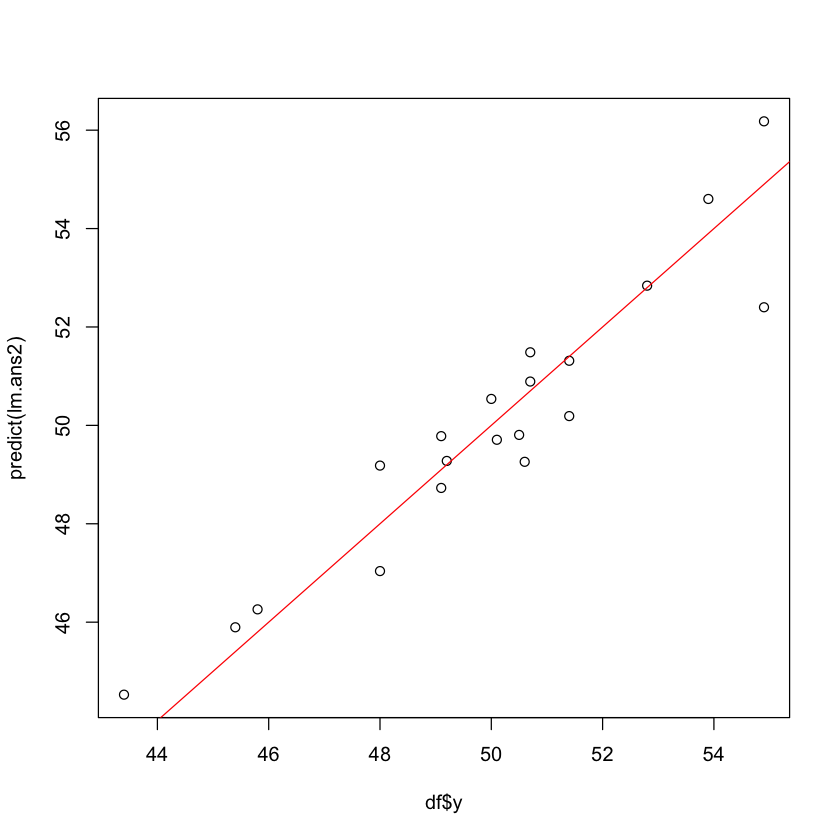
なんということだ。x1, x2, x3 ともに,偏回帰係数は有意ということになった。それもすさまじい p 値で。
決定係数は 0.9 近いし,自由度調整済みの決定係数だって 0.87 だ。
当然,回帰の分散分析だって,有意だ。
実測値と予測値の図を見るまでもない。
plot(df$y, predict(lm.ans2))
abline(0, 1, col="red")
ところで,重回帰分析にはまだまだ深い闇(なぞ)がある。
上の重回帰分析の結果で,x3 の偏回帰係数は -0.5355 と,負だよね。y と x3 の相関係数は 0.0979 だったのにね。
このなぞをちゃんと説明できないと,先には進めないよ。