サイコロを振って出た目の平均値を求める

$n$ 個のサイコロを $m$ 回振り，結果を $m \times n$ 行列に記録する。

行方向の平均値は mean(行列, dims=2) で求められる。但し，結果は $m \times 1$ 行列なので，必要ならベクトルに変換する。

これを，1 行で書く。

means(n, m=10000) = mean(rand(1:6, m, n), dims=2);

using Plots
function f(n, m=10000)
    x = means(n, m)
    histogram(x, normalize=:pdf, ylabel="pdf", xlabel="mean of $n dice", label="")
    println("mean = $(mean(x)), sd = $(std(x, corrected=false))")
    savefig("fig$n.png")
end

f (generic function with 2 methods)

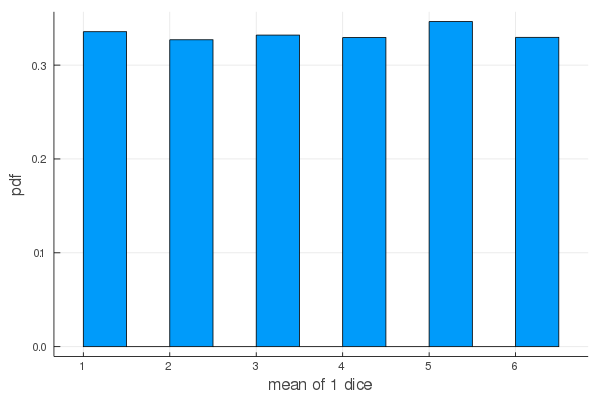
1 個のダイス¹の場合は一様分布だが，要するに度数分布に過ぎない。

平均値と標準偏差の理論値は 3.5 と std(1:6, corrected=false) = 1.707825127659933

f(1)

mean = 3.5064, sd = 1.7084961340313296

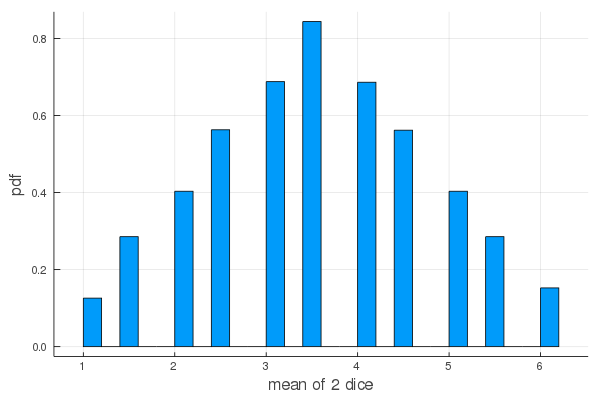
2 個では，三角分布。

f(2)

mean = 3.5129, sd = 1.2089803927276899

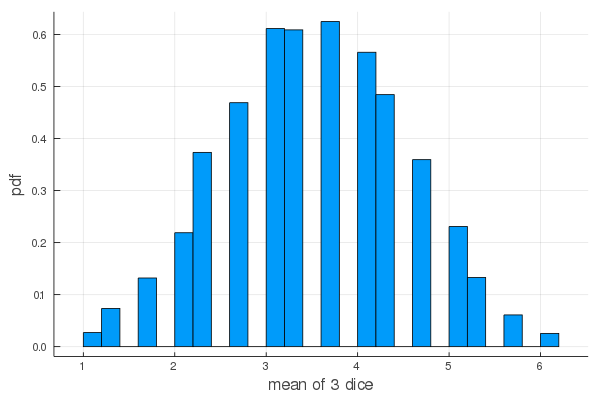
3 個だと，だんだん山型になる。

f(3)

mean = 3.4931, sd = 0.9849857026599138

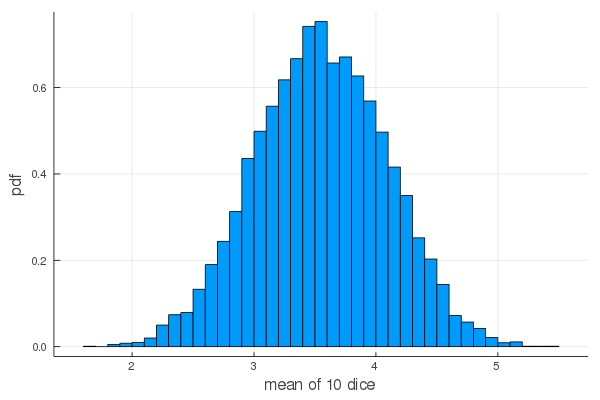
f(10)

mean = 3.5003, sd = 0.5366059168514636

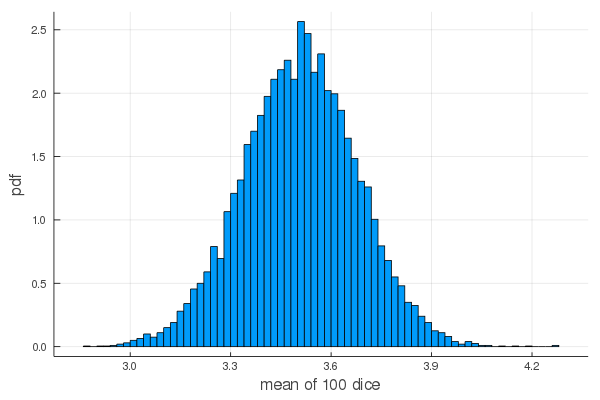
f(100)

mean = 3.5018859999999994, sd = 0.17010791575937903

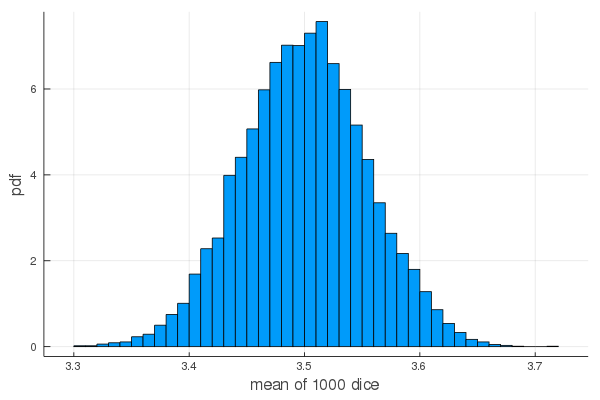
f(1000)

mean = 3.4995860999999997, sd = 0.05413639429062486

$n = 1000$ のときの標準偏差の理論値は $n = 1$ のときの標準偏差の $1/\sqrt{1000}$ 倍。

std(1:6, corrected=false) / sqrt(1000)

0.05400617248673217

中央極限定理

母集団の分布がどんな分布であっても、その誤差は標本の大きさを大きくしたとき近似的に正規分布に従う。

母分布から $n$ 個のデータを抽出して標本平均を求めたとき，標本平均の平均値は母分布の平均値（母平均），標本平均の標準偏差は「母分布の標準偏差（母標準偏差）/ $\sqrt{n}$」になる。

1. dice は複数形なので，「1 個のダイス」というのはおかしな言い方だそうだ。 ↩