pysparkで線形回帰モデル作成までの一連の流れを実行する
統計を勉強している人で線形回帰モデルを知らない人はいないと思います。pythonでもscikit-learnなどで簡単にモデリングできます。しかし、仕事などで大規模なデータを扱うとき、pysparkを使って線形回帰モデルを作成したいときもあると思います。私もその一人ですが、ネットで調べてもなかなか情報が少なかったり、英語ばかりで辛かったです。そこで、私が調べた内容を備忘録的にまとめておきます。
今回は線形回帰モデルを下記のステップに分けて作成・評価しました。
- モデル作成のための準備
- 基本統計量の確認
- データの標準化 OR 正規化
- 多重共線性の排除
- モデル作成
- モデル評価
- 線形回帰モデルの仮定を満たしているかの確認
- 残差の分散は均一か?
- 残差が正規分布にしたがっているか?
- モデル選択基準
- AICの計算
- 汎化性能の計算
- 線形回帰モデルの仮定を満たしているかの確認
各ステップで必要な関数はpysparkで実装されていなければ、自分で作成しました。作成した関数については、scikit-learnを用いて計算した場合の数値と比較し、出力値に差異がないことを確認していますが、使用は自己責任でお願いします。
実装時に使用したデータはボストンの住宅価格データセットです。下記のスクリプトを用いて、pyspark.DataFrameに変換しています。また実行環境は、google colabratory上のpyspark環境です。環境構築はこちらを参考にしました。
# pyspark関連のライブラリimport
import findspark
findspark.init()
from pyspark import SparkContext
sc = SparkContext.getOrCreate()
import pyspark
from pyspark.sql import SparkSession
spark = SparkSession.builder.getOrCreate()
# ボストンの住宅価格データセットの読み込み
from sklearn.datasets import load_boston
dataset = load_boston()
# ボストンの住宅価格データセットをpandas.DataFrameに変換
import pandas as pd
# 説明変数取得
data_x = pd.DataFrame(dataset.data,columns=dataset.feature_names)
# 目的変数を取得
data_y = pd.DataFrame(dataset.target,columns=['target'])
# 説明変数と目的変数を結合して、1つのDataFrameにする
data = pd.merge(data_y, data_x, how="left", left_index=True, right_index=True)
# pysparkDataFrameに変換
df = spark.createDataFrame(data)
なお、私がgoogle colaboratoryで実行したところ途中でメモリが不足し一旦Googleドライブにデータを出力して再読み込みをした箇所がいくつかあります。どこで出力したかと、出力のためのスクリプトを記載すると本質から離れるため割愛しています。
モデル作成のための準備
基本統計量の確認
線形回帰モデルを作る前に、データに含まれる変数の基本統計量を確認します。今回は、基本統計量として、各カラムの行数・平均・分散・最小値・最大値・欠損値の個数を計算します。
まずは行数です。count関数を使うだけなので容易です。
# 行数の確認
print("行数:", df.count())
次に、平均・分散・最小値・最大値を計算します。pyspark.mllib.stat.Statisticsを使うのですが、DataFrameをRDDに変換して使います。
# import
from pyspark.mllib.stat import Statistics
df_rdd = df.rdd #DataFrame → rddに変換
summary = Statistics.colStats(df_rdd) #colStatsインスタンス作成
# 基本統計量をpandas.DataFrameに格納する
summary_df = pd.DataFrame(columns = data.columns)
summary_df.loc["mean"] = summary.mean() #各列の平均
summary_df.loc["variance"] = summary.variance() #各列の分散
summary_df.loc["min"] = summary.min() #各列の最小値
summary_df.loc["max"] = summary.max() #各列の最大値
実はこの方法は環境に依存するみたいで、上記の方法でできない場合は以下を試してみてください。
# import
import numpy as np
# colStatsに格納できる形に変換
np_data = df.toPandas().values # pyspark.Dataframe →pandas.DataFrame → np.arrayに変換
df_from_np = sc.parallelize(np_data) #np.array → rddに変換
summary = Statistics.colStats(df_from_np) #colStatsインスタンス作成
# 基本統計量をpandas.DataFrameに格納する
# 一つ上のスクリプトと同じ
この方法はpandasやnumpyを経由するので、これも環境に依存してできないこともあるかもしれません。そのときは残念ながら、groupbyを用いてカラムごとに基本統計量を計算する必要があります。「pyspark groupby」で調べると記事がたくさんあるので、ここでは説明を割愛します。
最後に欠損値の個数の計算です。
# 各列の欠損値の個数の確認
from pyspark.sql.functions import col
null_count_list = [df.where(col(c).isNull()).count() for c in df.columns] #各列の欠損値の個数を計算
null_count_df = pd.DataFrame(columns = df.columns) #欠損値の個数を格納するdataFrameを作成
null_count_df.loc["null_count"] = null_count_list
データの標準化 OR 正規化
ここでは、データの標準化と正規化の方法を説明します。これを行うことで線形回帰モデルに含まれるパラメータの大きさを適切に比較できるようになります。なお、ここでいう標準化はZスコア化、正規化はmin-maxスケーリングを行うことを指します。
まずデータにIDを振っておきます。これは後々便利になるための作業で、本質的ではないです。
# IDを振っておく(便利のため)
# import
from pyspark.sql.functions import monotonically_increasing_id
# IDを連番で振る
df_id = df.withColumn('ID', monotonically_increasing_id())
標準化
標準化するためのスクリプトは下記です。
# import
from pyspark.sql import functions as F
from pyspark.sql.window import Window
# 目的変数、説明変数の抽出
var = df_id.columns
var.remove("ID") #ID列を排除
# 標準化
z_df = df_id
for c in var:
tmp1_z_df = (
df_id
.withColumn('mean', F.mean(c).over(Window.orderBy()))
.withColumn('std', F.stddev(c).over(Window.orderBy()))
.withColumn(c+'_z_scaled', (F.col(c) - F.col('mean')) / F.col('std'))
)
tmp2_z_df = tmp1_z_df.select("ID", c+"_z_scaled")
z_df = z_df.join(tmp2_z_df, ["ID"], "left")
ちなみに、標準化するためのクラスとして、pyspark.ml.feature.StandardScalerがあります。しかし、業務で使ったときに標準化後のデータをparquet形式で保存しようとしたところエラーを吐いて動かなくなりました。そのため、今回は時間がかかりますが、カラムを一つ一つ標準化していく方法を紹介しました。
正規化
正規化するためのスクリプトは下記です。
# 正規化
Mm_df = df_id
for c in var:
tmp1_Mm_df = (
df_id
.withColumn('max', F.max(c).over(Window.orderBy()))
.withColumn('min', F.min(c).over(Window.orderBy()))
.withColumn(c+'_Mm_scaled', (F.col(c) - F.col('min')) / (F.col('max')-F.col('min')))
)
tmp2_Mm_df = tmp1_Mm_df.select("ID", c+"_Mm_scaled")
Mm_df = Mm_df.join(tmp2_Mm_df, ["ID"], "left")
これも標準化と同じようにpyspark.ml.feature.MinMaxScalerが存在しますが、StandardScalerと同じ理由で上記スクリプトを紹介しました。
多重共線性の排除
線形回帰モデルにおいて変数間に相関がある場合は、相関がある変数のうちの一つを取り除く必要があります。ここでは、VIFを用いて相関の有無を確認しようと思います。VIFについてはこちらを参照しました。なお、ここでは標準化したデータに対してVIFを求めています。途中でfeaturesうんぬんと出てくるのですが、これについては「モデル作成」の章で説明します。
# import
from pyspark.ml.feature import VectorAssembler
from pyspark.ml.regression import LinearRegression
# VIFを格納するリスト
VIF_intercept_list = [] # VIFを求める際の線形回帰モデルにおいて、定数項を入れる
VIF_not_intercept_list = [] # VIFを求める際の線形回帰モデルにおいて、定数項を入れない
# 説明変数の取得
tmp_ex_var = z_df.columns
ex_var = [ev for ev in tmp_ex_var if "_z_scaled" in ev]
ex_var.remove("target_z_scaled")
# VIFの計算
for c in ex_var:
# featuresの作成(pysparkのLinearRegressionにおいては、説明変数をベクトル化し一つのカラムにする必要がある)
##VIF計算時に説明変数となる変数の取得
VIF_ex_var = [c2 for c2 in ex_var if c2 != c]
## VectorAssemblerインスタンス作成
vector_assembler = VectorAssembler(
inputCols = VIF_ex_var, #線形回帰モデルの説明変数
outputCol='features' # 説明変数をベクトル化したカラム
)
## features化したpyspark.DataFrameの作成
VIF_z_df = (
vector_assembler
.transform(z_df)
.withColumnRenamed(c, "label")
)
# 線形回帰
## 定数項ありバージョン
lr_intercept = LinearRegression(regParam = 0.0, fitIntercept = True)
lrModel_intercept = lr_intercept.fit(VIF_z_df)
trainig_summary_intercept = lrModel_intercept.summary
## 定数項なしバージョン
lr_not_intercept = LinearRegression(regParam = 0.0, fitIntercept = False)
lrModel_not_intercept = lr_not_intercept.fit(VIF_z_df)
trainig_summary_not_intercept = lrModel_not_intercept.summary
## VIFの計算
VIF_intercept_list.append(1/(1-trainig_summary_intercept.r2))
VIF_not_intercept_list.append(1/(1-trainig_summary_not_intercept.r2))
## 今何を計算しているか可視化
print("目的変数:", c, "\n")
print("説明変数:", VIF_ex_var, "\n")
# pandasDataFrameに格納してVIFを見やすくする
VIF_df = pd.DataFrame(index = ex_var)
VIF_df["VIF_intercept"] = VIF_intercept_list # 定数項を入れた線形回帰モデルから得られたVIF
VIF_df["VIF_not_intercept"] = VIF_not_intercept_list # 定数項を入れない線形回帰モデルから得られたVIF
今回は$VIF\geq10$の変数がなかったので、説明変数を取り除くことはせずに次に進みました。
モデル作成
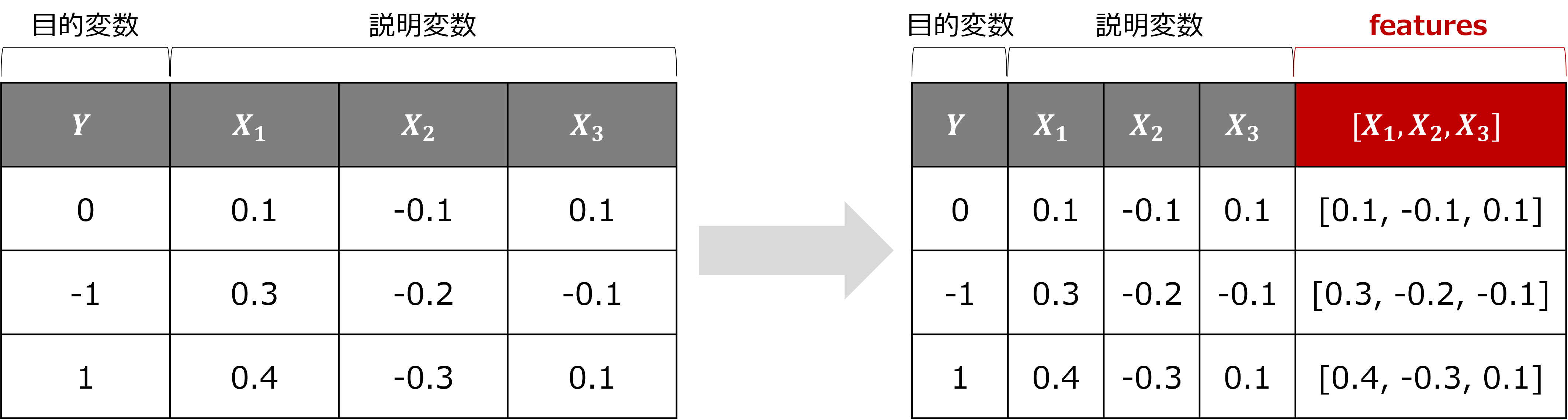
pysparkで線形回帰モデルを作成する際に、ちょっと癖があると思ったのが説明変数をまとめたカラムを作成する必要があることです。下図の左側が元々のpyspark.DataFrameです(数値は適当です)。そして右側がfeaturesを含めたpyspark.DataFrameです。pysparkでLinearRegressionを使う場合には、このfeaturesを作成する必要があります。
featuresを作成するためのスクリプトが下記です。
# import
from pyspark.ml.feature import VectorAssembler
# featuresの作成
# ex_varは説明変数のカラム名を入れたリスト
vector_assembler = VectorAssembler(
inputCols = ex_var, # featuresに入れたいカラムをリストで指定
outputCol='features'
)
feature_z_df = (
vector_assembler
.transform(z_df) # featuresが含まれたpyspark.DataFrameの作成
.withColumnRenamed(target_var, "label") # LinearRegressionで指定する目的変数のdefaultがlabelなのでlabelにカラム名を変えた。
)
ここまできたら、feature_z_dfをLinearRegressionに突っ込めば線形回帰モデルが作成できます。LinearRegressionを使う上で迷った引数を下記にまとめておきます。本当は引数の意味をもっとちゃんと理解したいのですが、下記の設定でscikit-learnで線形回帰モデルを実行した結果と一致しました。
| 引数 | 意味 |
|---|---|
| featuresCol | 説明変数のカラム名を指定。defaultは"features"。 |
| labelCol | 目的変数のカラム名を指定。defaultは"label"。 |
| regParam | 正則化項の係数。defaultは0。 |
| fitIntercept | 定数項をいれるか否か。Trueだと定数項あり、Falseだと定数項なし。defaultはTrue。 |
今回については説明変数のカラム名はfeatures、目的変数のカラムはlabelなので、featuresColとlabelColは明示的に指定していません。また、RidgeやLassoをしたいわけではないので、正則化項は0にしました。また、定数項も入れました。線形回帰モデルを作成するスクリプトは下記です。
# 定数項ありで線形回帰モデルの作成
lr = LinearRegression(regParam = 0.0, fitIntercept = True)
lrModel = lr_intercept.fit(feature_z_df)
また、作成したモデルに対して予測値を計算するスクリプトは下記です。
# 予測値の計算
predict_summary = lrModel.evaluate(feature_z_df)
モデル評価
ここでは作成した線形回帰モデルの評価を行います。最初に謝っておきますが、「線形回帰モデルの仮定を満たしているかの確認」内の「残差の分散は均一か?」「残差が正規分布にしたがっているか?」では、pandas.DataFrameを使っています。もし、pysparkで散布図を書けるのであればpandas.DataFrameを使う必要はないのですが...。私が調べたところそのようなパッケージを発見することはできませんでした。
線形回帰モデルの仮定を満たしているかの確認
残差の分散は均一か?
残差の分散が均一か確認するために散布図を作成しました。スクリプトは下記です。
# ダウンサンプリング & Pandasに変換
sampled_predict_residuals_pd_df = (
predict_residuals_df
.select("prediction", "residuals")
.sample(1.00) #ダウンサンプリング(今回はデータ量が少ないので、ダウンサンプリングしていない)
.toPandas() #Pandasに変換
)
# 散布図(予測値×残差)作成
import matplotlib.pyplot as plt
plt.scatter(sampled_predict_residuals_pd_df["prediction"], sampled_predict_residuals_pd_df["residuals"])
plt.axhline(y = 0, xmin = min(sampled_predict_residuals_pd_df["prediction"]), xmax = max(sampled_predict_residuals_pd_df["prediction"]), color = "black", linestyle = "dotted")
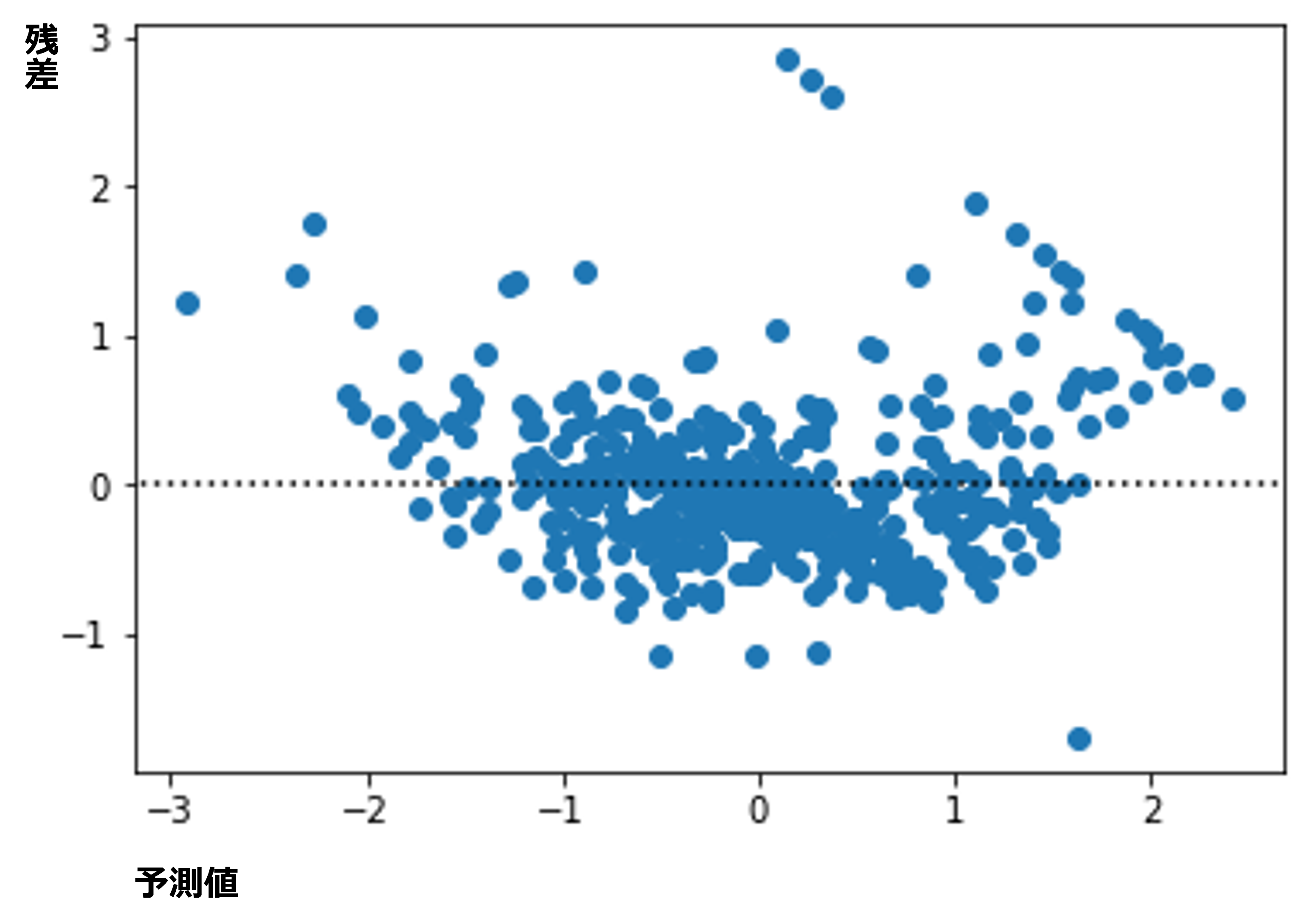
このスクリプトで得られた散布図は下記です。この図を見ると予測値が-2以下と1.5以上で分散が均一ではなさそうに見えます。今回は、単純に線形回帰モデルの仮定を満たしているかどうか確認する図を作成したかったので、これ以上深追いしません。しかし、仮定を満たしているか微妙なところです。
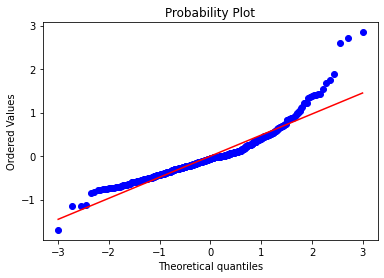
残差が正規分布にしたがっているか?
ここではQQプロットを作成して確認します。スクリプトは下記です。
# QQプロット作成
## 値の作成
import scipy.stats as stats
stats.probplot(sampled_predict_residuals_pd_df["residuals"], dist = "norm", plot = plt)
plt.show()
モデル選択基準
ここではAICと汎化性能を求めました。線形回帰モデルなので、係数が0かどうかの検定も作成したかったのですが、時間の都合から割愛します。係数が0かどうかの検定を実行するためのスクリプトはまた時間ができたときにでも作成します。
AICの計算
線形回帰モデルにおけるAICの計算をするスクリプトです。誤差項が平均0、分散が一定の正規分布にしたがっていることを仮定しています。今回は$AIC = 780.3$になりました。
# サンプルサイズ
N= feature_z_df.count()
# パラメータの個数
k = len(ex_var)+1 # 定数項がある場合
# k = len(ex_var) # 定数項がない場合
# 残差の2乗和の計算
var_hat = (
predict_residuals_df
.withColumn("residulas_2", col("residuals")**2)
.groupby()
.agg(
F.sum("residulas_2").alias("sum_residulas_2")
)
.collect()[0]
.sum_residulas_2
)/(N-k)
# AICの計算
from math import log, sqrt, pi
AIC = -2*N*log(1/sqrt(2*pi*var_hat))+N+k
print("AIC = ", AIC)
汎化性能の測定
汎化性能を計算するためのスクリプトは下記です。今回はRMSEを計算しています。今回は$RMSE = 0.45$でした。
また、ホールドアウト法で実装しています。クロスバリデーションをしたい場合は、for文で全体を包むなどして実装してください。
# 訓練データとテストデータに分割
feature_z_df_train, feature_z_df_test = feature_z_df.randomSplit([0.8, 0.2], seed=2021)
# 訓練データについて定数項ありで線形回帰モデルの作成
lr = LinearRegression(regParam = 0.0, fitIntercept = True)
lrModel_train = lr_intercept.fit(feature_z_df_train)
# テストデータについて予測値の計算
predict_summary_test = lrModel_train.evaluate(feature_z_df_test)
predict_df_test = predict_summary_test.predictions
# RMSEの計算
## 予測値と実際の値を一つのdataFrameにまとめる
feature_z_df_test_id = feature_z_df_test.select("ID", "label")
predict_df_test_id = predict_df_test.select("ID", "prediction")
# 実績値・予測値の両方が入ったDataFrameの結合
predict_act_df_test = (
feature_z_df_test_id
.join(predict_df_test_id,
["ID"],
"left"
)
.select("label", "prediction")
)
# RMSEの計算
from pyspark.mllib.evaluation import RegressionMetrics
metrics = RegressionMetrics(predict_act_df_test.rdd)
print("RMSE = %s" % metrics.rootMeanSquaredError)