誤差逆伝播の数式を追う(Juliaのコードつき)

はじめに

　本記事は、深層学習（Deep Learning:以下DL）の初学者である私が、誤差逆伝播を理解する過程で学んだことを記したものです。私の場合、誤差逆伝播によるパラメータの更新式の導出に非常に時間がかかりました。そこで、本記事は、誤差逆伝播について数式を用いて説明するものの、読者が行間を埋める必要がないような（つまり、上から読んでいけば理解できるような）ものにすることを目指します。

対象読者

　本記事の対象読者は、誤差逆伝播を数式レベルで理解したい方です。したがって、本記事はPytorchなどを使ってとりあえず実装をしたいという方には向いていません。また、数式レベルで理解するための前提知識として、行列の計算や偏微分の知識が必要です。

問題設定

　　下記の問題設定で誤差逆伝播について説明していきます。なお、下記の問題設定はなっとく！ディープラーニングから拝借してきました。より詳しく知りたい方は本書をご覧ください。

• データセット：MNISTデータセット
• 解きたい問題：分類問題。MNISTデータセットに含まれる手書き文字の判別を行う
• 解くための手段：3層のDL

　上記について補足します。
　まず、MNISTデータセットとは、 0~9の手書き数字の画像のデータセットです。機械学習のチュートリアルなどでよく使われています。このデータセットは、7万枚の幅28×高さ28のグレースケールの画像データから構成されています。詳細は、MNIST：手書き数字の画像データセットをご覧ください。
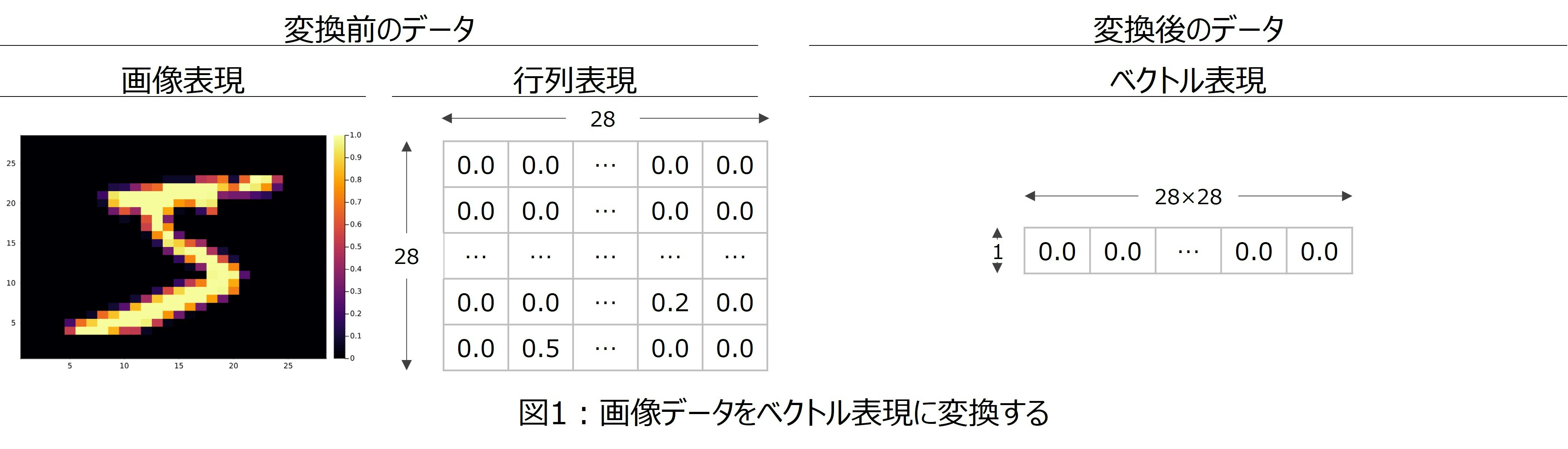
　今回は、幅28×高さ28のデータを、28×28=1×784のベクトルに変換して使おうと思います（図1）。

　次に、解きたい問題について補足します。今回MNISTデータセットを使って、手書き文字の判別をしようと思います。そこで、今回はOne Hot Encodingしたデータを使います。
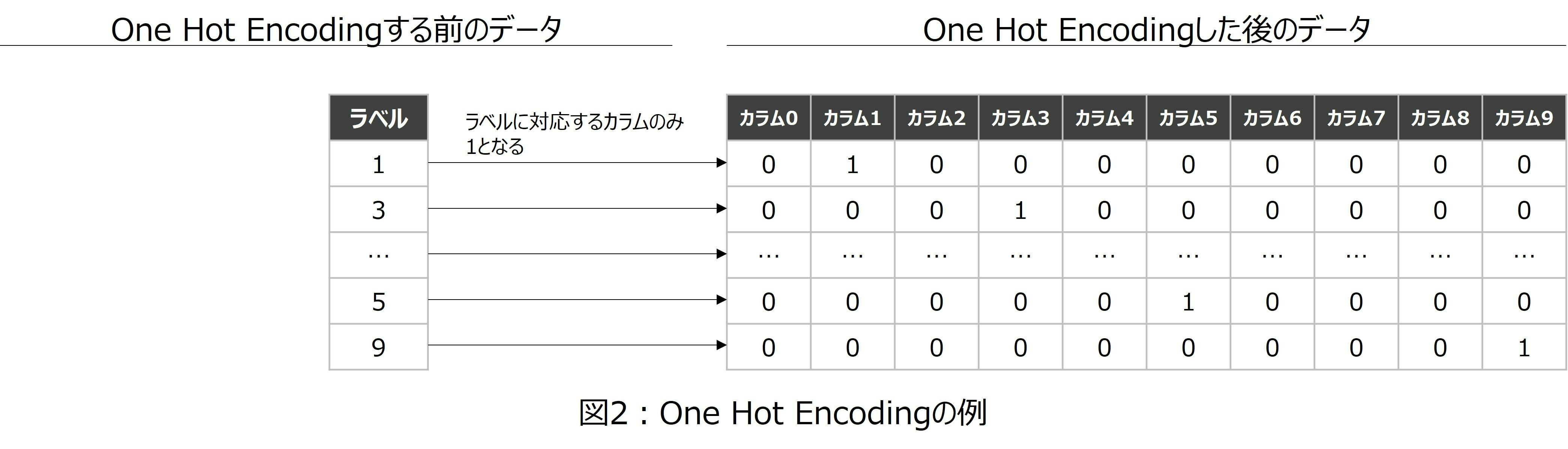
　One Hot Encodingとは、該当のカラムの値だけを1、それ以外のカラムの値を0にしたものになります。One Hot Encodingの例を図2に示します。

　最後に、解くための手段について補足します。今回はシンプルな3層構造のニューラルネットワークを使おうと思っています。具体的には、第1層は入力層で784個のノードがあります。第2層は隠れ層で300個のノードがあります。また、活性化関数としてReLu関数を用います。そして第3層は出力層で10個のノードがあります。
なお、活性化関数として使うReLu関数とは、

\begin{eqnarray}
{\rm ReLu}(x) = \left\{
\begin{array}{ll}
1 & (x \geq 0) \\
0 & (x \lt 0)
\end{array}
\right. \tag{1}
\end{eqnarray}

という形の関数です。
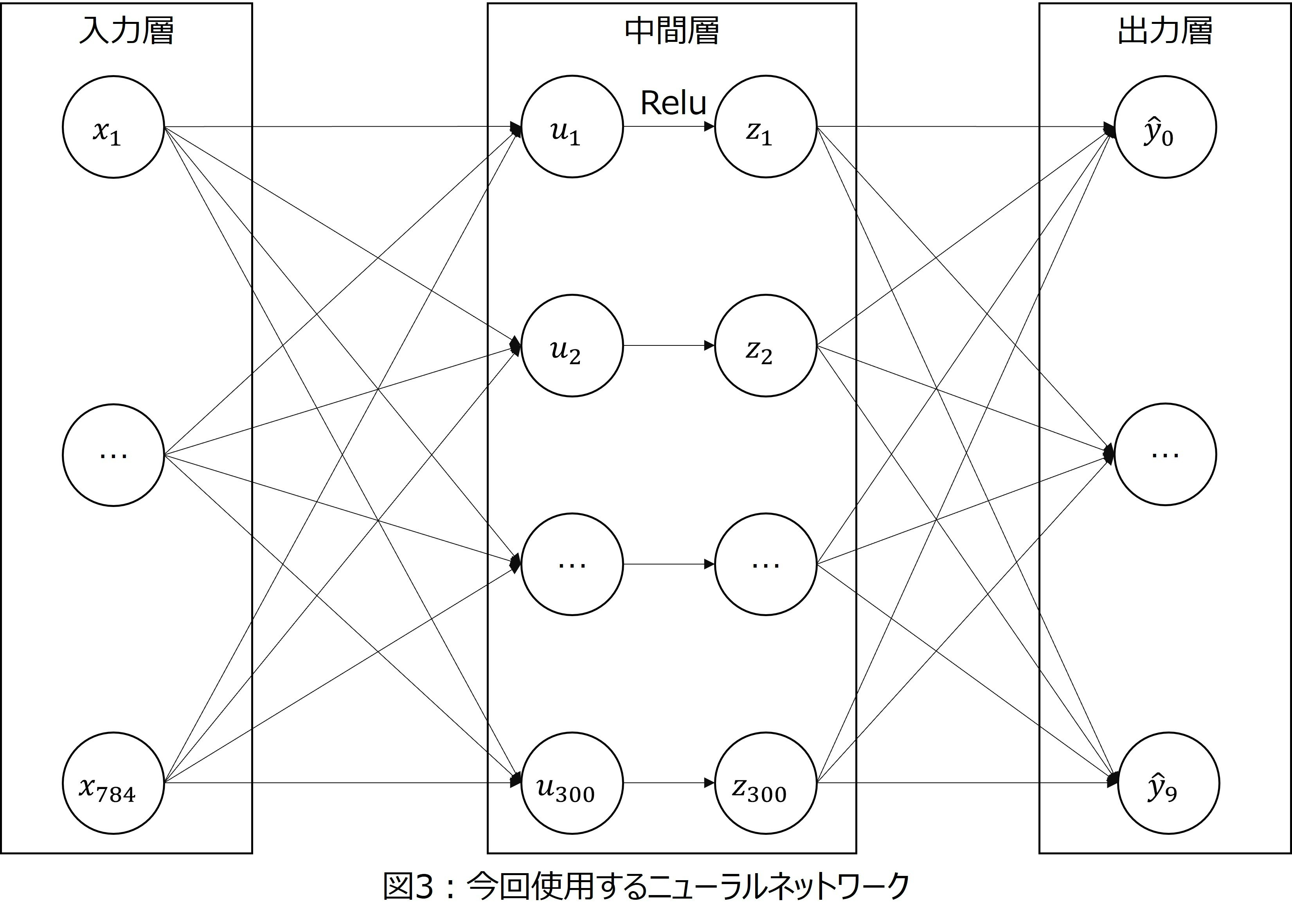
　今回使う3層構造のニューラルネットワークを図3に示します。

　以上のニューラルネットワークにおけるパラメータを更新するための、更新式を導出することが本記事の目的となります。

ニューラルネットワークに出てくる文字の説明

　今回使うニューラルネットワークに出てくる文字もここで整理しておこうと思います。

• 1つの入力データを$\boldsymbol{x}$と表現します。これは、1×784の行列です。
• 第1層と第2層の間のパラメータを$W$と表現します。これは、784×300の行列です。
• 第2層の入力データを$\boldsymbol{u}$と表現します。これは、1×300の行列です。
• 第2層の入力データを活性化関数ReLuで変換した後の値を$\boldsymbol{z}$と表現します。これも$\boldsymbol{u}$と同じ1×300の行列です。
• 第2層と第3層の間のパラメータを$\Theta$と表現します。これは、300×10の行列です。
• 第3層で出力される予測値を$\boldsymbol{\hat{y}}$と表現します。これは1×10の行列です。
• 教師データの教師ラベルを$\boldsymbol{y}$と表現します。これは1×10の行列です。
• 損失関数を$L$とし、二乗誤差を用います。

　これらの文字間には次のような関係があります。

• 第1層から第2層への変換：$\boldsymbol{u} = \boldsymbol{x}W$
• 第2層での活性化関数による変換：$z_i = {\rm ReLu}(u_i)$
• 第2層から第3層への変換：$\boldsymbol{\hat{y}} = \boldsymbol{z}\Theta$
• 損失関数：$L=\displaystyle{\sum_{k=0}^9}(\hat{y}_k-y_k)^2$

前提知識

　本節では、誤差逆伝播の式を導出するために必要な前提知識として、勾配降下法について説明しようと思います。

勾配降下法

　勾配降下法とは、最適化アルゴリズムの一つです。最適化したい関数の最小化をするために利用されます。
　ニューラルネットワークの文脈でいえば、最適化したい関数とは損失関数です。損失関数$L$はニューラルネットワークに含まれるパラメータ（ここでは$\beta$とします）の関数です。
　このとき、$L(\beta)$を$\beta$について最適化するために、以下の更新式を用いる手法を勾配降下法といいます。

\begin{eqnarray}
\beta^{(n+1)} = \beta^{(n)} - \eta \dfrac{\partial L(\beta^{(n)})}{\partial \beta} \tag{2}
\end{eqnarray}

なお、$\eta$は学習率と呼ばれるパラメータで、正の値をとります。この$\eta$については後ほど説明します。
　(2)式で関数の最小化ができる理由を説明します。シンプルな二次関数を例として考えていきます。
$L(\beta) = \beta^2$とします。このとき、$\dfrac{\partial L(\beta^{(n)})}{\partial \beta} = 2\beta$なので、更新式は

\begin{eqnarray}
\beta^{(n+1)} = \beta^{(n)} - 2\eta \beta^{(n)}  \tag{3}
\end{eqnarray}

となります。
　さて、ここで$\beta^{(n)}>0$のときを考えます。このとき、$L(\beta) = \beta^2$の最適解は$\beta=0$であることを考えると、更新後の$\beta^{(n+1)}$は、更新前の$\beta^{(n)}$よりも小さくなっていて欲しいはずです。実際に(3)式を見てみると、$\beta^{(n)}>0$のとき、$- 2\eta \beta^{(n)} < 0$なので$\beta^{(n+1)} < \beta^{(n)}$となっています。
　同様に$\beta^{(n)}<0$のときを考えます。このときは、$\beta^{(n)}>0$のときとは逆で$\beta^{(n+1)} > \beta^{(n)}$となってほしいです。実際に(3)式を見てみると、$\beta^{(n)}<0$のとき、$- 2\eta \beta^{(n)} > 0$なので$\beta^{(n+1)} > \beta^{(n)}$となっています。
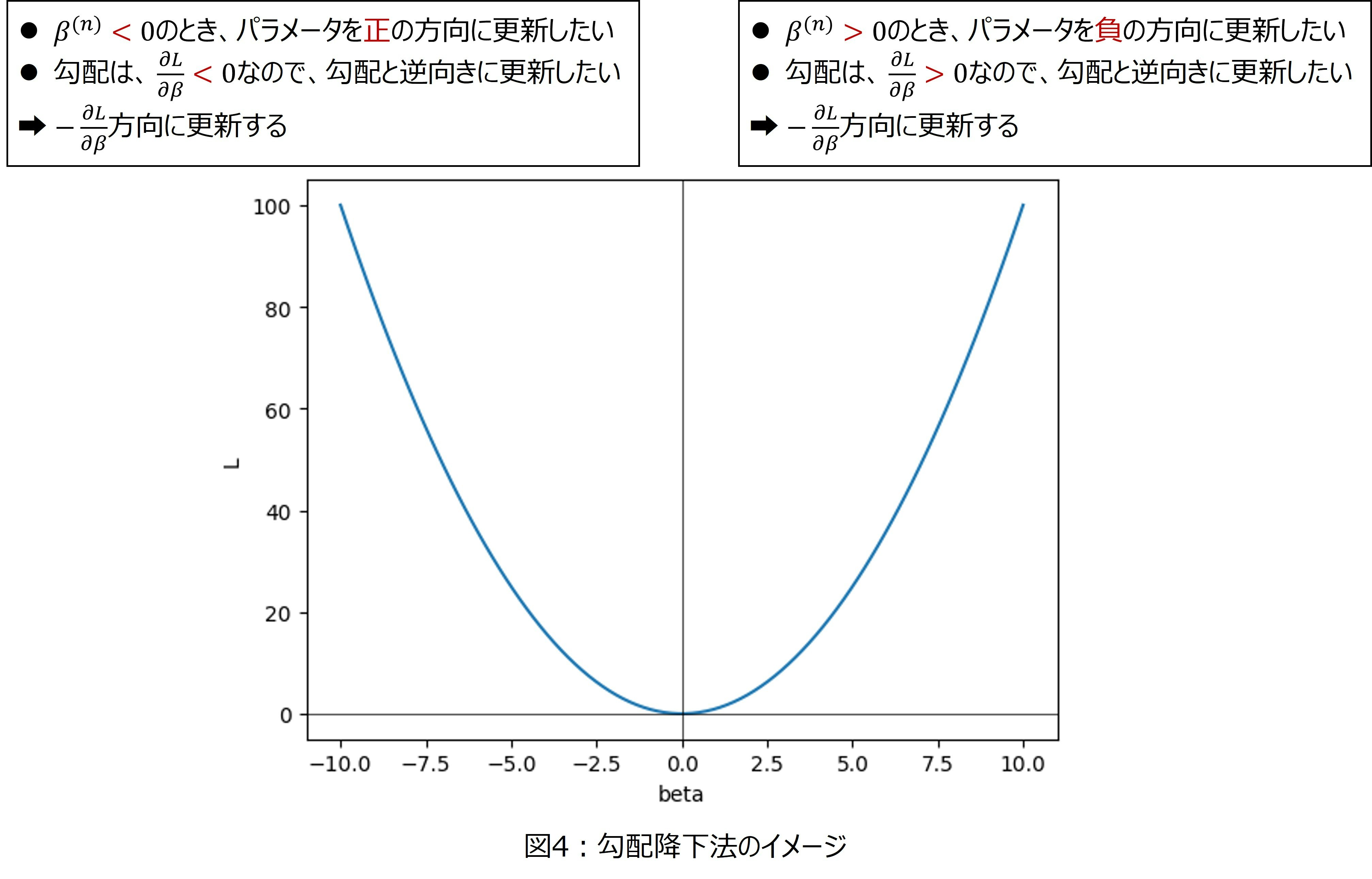
　ここでポイントなるのは、$\dfrac{\partial L(\beta^{(n)})}{\partial \beta}$が勾配の更新方向を決めているということです。図4を見て頂くとわかるように、$\beta^{(n)}$が最適解より大きい場合、

• 更新方向は負であって欲しい
• 勾配の値（1回微分の値）は正
  となります。同様に、$\beta^{(n)}$が最適解より小さい場合、
• 更新方向は正であって欲しい
• 勾配の値は負
  となっています。

　したがって、更新方向と勾配の値は正負逆転しています。パラメータを更新する際に$-\eta \dfrac{\partial L(\beta^{(n)})}{\partial \beta}$で更新するのは、このためです。つまり、$\dfrac{\partial L(\beta^{(n)})}{\partial \beta}$はパラメータの更新方向を決めています。
　次に学習率$\eta$の意味を説明します。学習率$\eta$は更新の大きさを決めています。これにより、最適解への収束の速さが決まります。
　例えば、$L(\beta) = \beta^2$において更新の初期値を$\beta^{(0)}=1$とします。このとき、各学習率の値ごとにパラメータを更新させていった結果が下記になります。

パラメータの更新回数	$\eta=0.01$	$\eta=0.1$	$\eta=1$	$\eta=10$
1回目	0.98	0.8	-1.0	-19
2回目	0.96	0.64	1.0	361
3回目	0.94	0.51	-1.0	-6,859
4回目	0.92	0.41	1.0	130,321
5回目	0.90	0.33	-1.0	-2,476,099
6回目	0.89	0.26	1.0	47,045,881
7回目	0.87	0.21	-1.0	$-8.9\times10^8$
8回目	0.85	0.17	1.0	$-1.7\times10^{10}$
9回目	0.83	0.13	-1.0	$-3.2\times10^{11}$
10回目	0.82	0.11	1.0	$6.13\times10^{12}$

　真値$\beta=0$に対して、学習率が小さすぎる場合（$\eta=0.01$の場合）、なかなかパラメータの更新が進まないことがわかります。また、学習率が大きすぎる場合（$\eta=1, 10$の場合）はパラメータが発散してしまって収束していないことがわかります。今回の場合は$\eta=0.1$くらいがちょうど良さそうです。
このように学習率はパラメータ更新の更新幅を決める役割を持っていることがわかります。

DLにおける勾配降下法の使い方

　DLにおける勾配降下法の使い方を説明します。DLにおいて、推定対象となるのはネットワークに含まれるパラメータです。本記事の問題設定でいえば、第1層と第2層の間のパラメータ$W$と第2層と第3層のパラメータ$\Theta$が推定対象です。
　損失関数をこれらのパラメータの関数として捉えることで、DLのパラメータ推定問題を最適化問題として捉えることができます。つまり、「予測精度が高いDLを構築する」という問題を、「損失関数$L$をパラメータ$(W, \Theta)$について最小化する」という問題に帰着させることができます。

勾配降下法の更新式の導出

　ここからが本番です。DLにおける勾配降下法の更新式を導出していきます。この更新式を導出するにあたり、知らなければならない前提知識がもう一つあります。その前提知識とは、合成関数の微分法です。

合成関数の微分法

合成関数とは以下のような関数です。

\begin{eqnarray}
y_j &=& g_j(x_1, x_2, \cdots, x_I)\ \ \ \ \ \ \ (j=1, \cdots, J) \\
z &=& f(y_1, \cdots, y_J)
\end{eqnarray}

このとき、以下が成り立ちます。

\begin{eqnarray}
\dfrac{\partial z}{\partial x_i} = \displaystyle{\sum_{j=1}^J}\dfrac{\partial y_j}{\partial x_i}\dfrac{\partial z}{\partial y_j}
\end{eqnarray}

今回はこれを使ってDLにおける勾配降下法の更新式を導出します。

第2層と第3層間のパラメータの更新式

　推定対象のパラメータは、第1層と第2層の間のパラメータ$W$と第2層と第3層の間のパラメータ$\Theta$です。本節では、この二つのパラメータの中で、更新式の導出が容易な$\Theta$について説明します。
今回導出したい式は、

\Theta^{(n+1)} = \Theta^{(n)}-\eta \dfrac{\partial L(\Theta^{(n)})}{\partial \Theta}

　です。この式の中で$\dfrac{\partial L(\Theta^{(n)})}{\partial \Theta}$が計算できればOKです。　
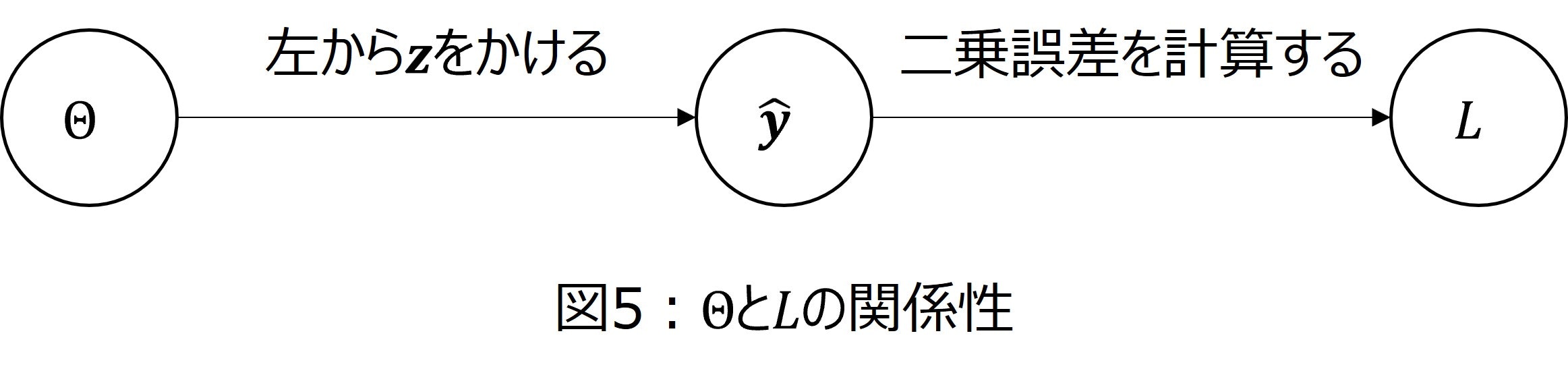
　実際に計算をしていきます。パラメータ$\Theta$と損失関数$L$の間には、図5の関係性があります。

　また、いきなり$\dfrac{\partial L(\Theta^{(n)})}{\partial \Theta}$を考えることは難しいので、$\Theta$の成分$\theta_{mn}$による微分を考えてみます。つまり、$\dfrac{\partial L}{\partial \theta_{mn}}$を考えます。このとき、図5の関係性と合成関数の微分法を使うことで

\dfrac{\partial L}{\partial \theta_{mn}} = \displaystyle{\sum_{k=0}^9}\dfrac{\partial L}{\partial \hat{y}_k}\dfrac{\partial \hat{y}_k}{\partial \theta_{mn}}

が成り立ちます。なので、ここから先は$\dfrac{\partial L}{\partial \hat{y}_k}$と$\dfrac{\partial \hat{y}_k}{\partial \theta _ {mn}}$に分けて考えます。
　まず、$\dfrac{\partial L}{\partial \hat{y}_k}$について考えます。今回損失関数として二乗誤差を用いているので、$L=(y_k-\hat{y}_k)^2$です。したがって、

\dfrac{\partial L}{\partial \hat{y}_k} = (-2)(y_k-\hat{y}_k)

となります。
　次に、$\dfrac{\partial \hat{y}_k}{\partial \theta _ {mn}}$について考えます。ここでは、$\boldsymbol{\hat{y}} = \boldsymbol{z}\Theta$を使います。これより、$\hat{y}_k=\displaystyle{\sum _ {i=1} ^{300}}\theta _ {ik}z_i$が成り立ちます。したがって、

\begin{eqnarray}
\dfrac{\partial \hat{y}_k}{\partial \theta_{mn}} = \left\{
\begin{array}
zz_m & (i=m, k=n) \\
0 & ({\rm otherwise})
\end{array}\right.
\end{eqnarray}

となります。
　以上より、

\dfrac{\partial L}{\partial \theta_{mn}} = -2(y_n-\hat{y}_n)z_m

となります。最後に$\dfrac{\partial L(\Theta^{(n)})}{\partial \Theta}$をベクトル表記すると、

\begin{eqnarray}
\dfrac{\partial L(\Theta^{(n)})}{\partial \Theta} &\propto& -\left(
\begin{array}
((y_0-\hat{y}_0)z_1 & \cdots & (y_9-\hat{y}_9)z_1 \\
\vdots & \ddots & \vdots \\
(y_0-\hat{y}_0)z_{300} & \cdots & (y_9-\hat{y}_9)z_{300}
\end{array}
\right) \\
&=& -\left(\begin{array}
zz_1 \\
\vdots \\
z_{300}
\end{array}\right)
\left(y_0-\hat{y}_0, \cdots, y_9-\hat{y}_9
\right) \\
&=& -\boldsymbol{z}^\top (\boldsymbol{y}-\boldsymbol{\hat{y}})
\end{eqnarray} 

となります。なお、係数の$-2$は学習率$\eta$で吸収できるので無視しました。

第1層と第2層間のパラメータの更新式

次に第2層と第3層の間のパラメータ$W$の更新式を導出します。こちらは、$\Theta$の更新式の導出と比べて難しく、一歩一歩数式を追っていく必要があります。
導出したい式は、$\Theta$のときと同様で

\dfrac{\partial L}{\partial W}

です。
　この式を導出するにあたり、$W$と$L$の関係性を明示しておきます（図6）。

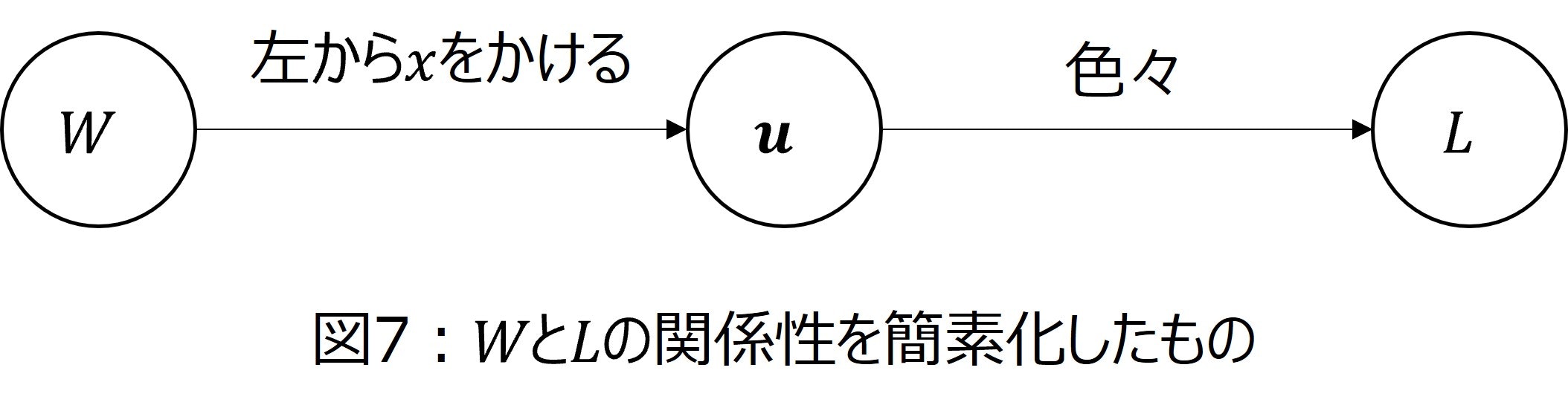
図6を見て頂くとわかるように、$W$から色々な処理をして$L$が計算されることが分かります。この「色々な処理」が$\dfrac{\partial L}{\partial W}$の導出を難しくしています。そこで、第二層の入力$\boldsymbol{u}$から損失関数$L$までの間を一つの関数とみなしてしまいます。この考え方を基に図6を捉え直すと、図7のようになります。

　また、$\Theta$のときと同様、いきなり$\dfrac{\partial L}{\partial W}$を導出することは難しいので、$W$の成分$w_{mn}$による微分$\dfrac{\partial L}{\partial w_{mn}}$を考えます。
　図7を見ながら合成関数の微分法を用いると、

\begin{eqnarray}
\dfrac{\partial L}{\partial w_{mn}} = \sum_{i=1}^{300}\dfrac{\partial L}{\partial u_i}\dfrac{\partial u_i}{\partial w_{mn}} \tag{4}
\end{eqnarray}

となります。そこで、この後は$\dfrac{\partial L}{\partial u_i}$と$\dfrac{\partial u_i}{\partial w_{mn}}$に分けて考えていきます。
　まず、簡単な$\dfrac{\partial u_i}{\partial w_{mn}}$について考えていきます。$\boldsymbol{u} = \boldsymbol{x}W$の関係から、

u_i = \sum_{l=1}^{784}x_l w_{li}

が成り立ちます。したがって、

\begin{eqnarray}
\dfrac{\partial u_i}{\partial w_{mn}} = \left\{
\begin{array}
xx_m & (l=m, i=n) \\
0 & ({\rm otherwise})
\end{array}
\right.
\end{eqnarray}

となります。以上より、(4)式は

\begin{eqnarray}
\dfrac{\partial L}{\partial w_{mn}} = \dfrac{\partial L}{\partial u_n}x_m \tag{5}
\end{eqnarray}

と割とシンプルな式に変形できます。
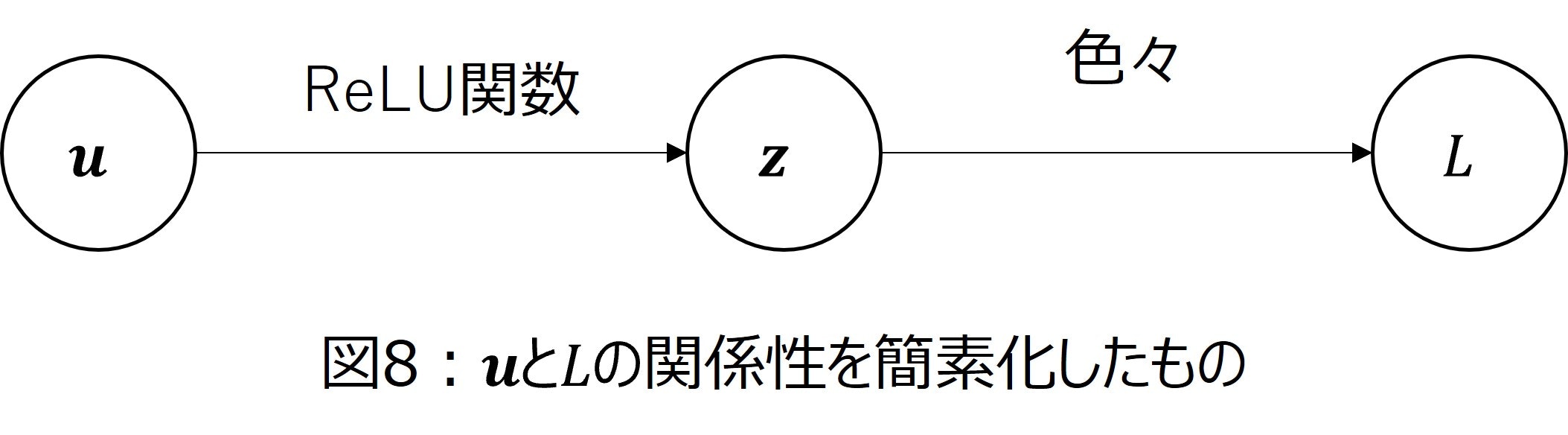
　次に、$\dfrac{\partial L}{\partial u_n}$を計算します。先ほどと同様に第2層の入力$\boldsymbol{u}$から損失関数$L$の関係のうち、必要な箇所だけを取り出したものが図8です。

　このとき、図8を使うことで

\begin{eqnarray}
\dfrac{\partial L}{\partial u_n} = \sum_{i=1}^{300} \dfrac{\partial L}{\partial z_i}\dfrac{\partial z_i}{\partial u_n} \tag{6}
\end{eqnarray}

となります。ここでも上記と同様に、$\dfrac{\partial z_i}{\partial u_n} $を考えていきます。これについては割と簡単で$z_n = {\rm ReLu}(u_n)$の関係があるので、

\begin{eqnarray}
\dfrac{\partial z_i}{\partial u_n} = \left\{
\begin{array}
a{\rm RD}(u_n) & (i=n) \\
0 & ({\rm otherwise})
\end{array}
\right.
\end{eqnarray}

となります。ただし、${\rm RD}$は${\rm ReLu}$を微分した関数で以下のように表すことができます。

\begin{eqnarray}
{\rm RD}(u_n) = \left\{\begin{array}
11 & (u_n \geq 0) \\
0 & (u_n < 0)
\end{array}\right.
\end{eqnarray}

以上より、(6)式は

\begin{eqnarray}
\dfrac{\partial L}{\partial w_{mn}} = \dfrac{\partial L}{\partial z_n}{\rm RD}(u_n)x_m \tag{7}
\end{eqnarray}

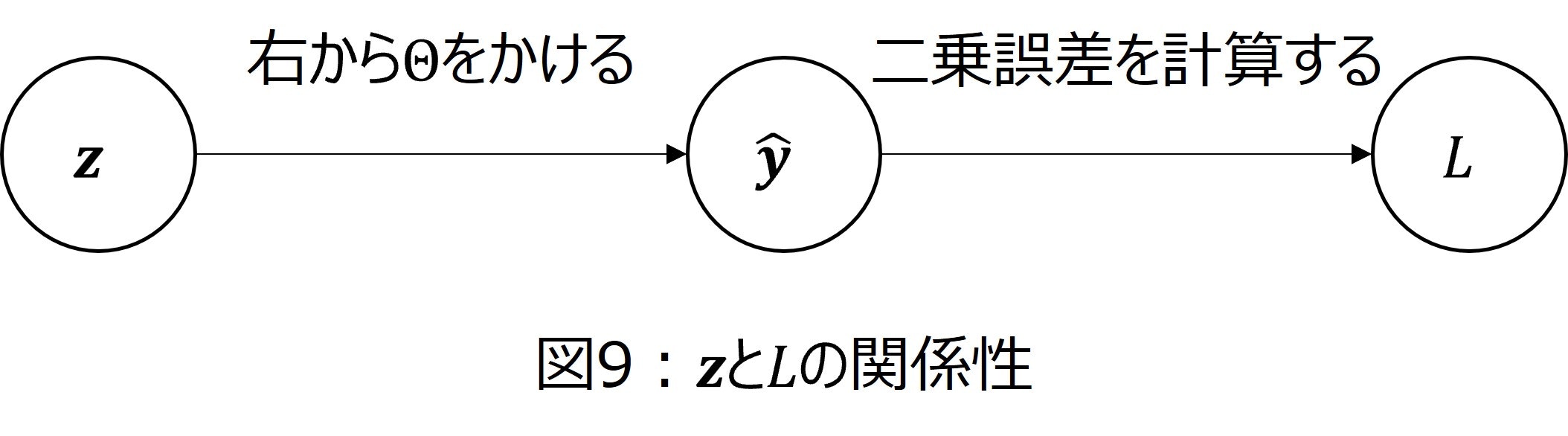
となります。最後に、$\dfrac{\partial L}{\partial z_n}$を計算します。第2層の出力$z_n$と損失関数$L$の関係は図9のようになります。

図9と合成関数の微分法を用いると

\dfrac{\partial L}{\partial z_n} = \sum_{k=0}^9 \dfrac{\partial L}{\partial \hat{y}_k} \dfrac{\partial \hat{y}_k}{\partial z_n}

が成り立ちます。ここで、
$L=(y_k-\hat{y}_k)^2$であることを用いると、$\dfrac{\partial L}{\partial \hat{y}_k} = (-2)(y_k-\hat{y}_k)$となります。また、$\hat{y}_k = \displaystyle{\sum _ {i=1}^{300}} \theta _ {ik}z _ i$を用いると

\begin{eqnarray}
\dfrac{\partial \hat{y}_k}{\partial z_n} = \left\{
\begin{array}
a\theta_{nk} & (i=n) \\
0 & ({\rm otherwise})
\end{array}\right.
\end{eqnarray}

となります。以上より、

\begin{eqnarray}
\dfrac{\partial L}{\partial z_n} = \sum_{k=0}^9 (-2)(y_k-\hat{y}_k)\theta_{nk} \tag{8}
\end{eqnarray}

となります。
　したがって、(7)、(8)式を用いると

\begin{eqnarray}
\dfrac{\partial L}{\partial w_{mn}} = \left\{ \sum_{k=0}^9(-2)(y_k-\hat{y}_k)\theta_{nk} \right\}{\rm RD}(u_n) x_m \tag{9}
\end{eqnarray}

となります。
　最後に、ここまで成分表記$\dfrac{\partial L}{\partial w_{mn}}$で書いてきた式を行列表記$\dfrac{\partial L}{\partial W}$に書き直して数式の導出を終わりにしたいと思います。
(9)式より

\begin{eqnarray}
\dfrac{\partial L}{\partial W} &\propto& -\left(\begin{array}
a\left( \sum_{k=0}^9 (y_k-\hat{y}_k)\theta_{1k}\right){\rm RD}(u_1)x_1 & \cdots & \left( \sum_{k=0}^9 (y_k-\hat{y}_k)\theta_{300k}\right){\rm RD}(u_{300})x_1 \\
\vdots & \ddots & \vdots \\
\left( \sum_{k=0}^9 (y_k-\hat{y}_k)\theta_{1k}\right){\rm RD}(u_1)x_{784} & \cdots & \left( \sum_{k=0}^9 (y_k-\hat{y}_k)\theta_{300k}\right){\rm RD}(u_{300})x_{784} \\
\end{array}\right) \\
&=& -\left(\begin{array}
xx_1 \\
\vdots \\
x_{784}
\end{array}\right)
\left(\sum_{k=0}^9 \left\{(y_k-\hat{y}_k)\theta_{1k}\right\}{\rm RD}(u_1) , \cdots, \sum_{k=0}^9 \left\{(y_k-\hat{y}_k)\theta_{300k}\right\}{\rm RD}(u_{300})\right) \\
&=& -\boldsymbol{x}^\top \left(\sum_{k=0}^9 (y_k-\hat{y}_k)\theta_{1k}\ , \cdots, \sum_{k=0}^9 (y_k-\hat{y}_k)\theta_{300k}\right) \odot \left({\rm RD}(u_1), \cdots, {\rm RD}(u_{300})\right) \\
&=& -\boldsymbol{x}^\top \left\{  (\boldsymbol{y}-\boldsymbol{\hat{y}}) \Theta^\top \odot {\rm RD}(\boldsymbol{u})\right\}
\end{eqnarray}

となります。ただし、$\odot$は成分の積を表す記号で下記で定義されるものです。

(a_1, a_2, \cdots, a_n)\odot (b_1, b_2, \cdots, b_n) = (a_1 b_1, a_2 b_2, \cdots, a_n b_n)

また、${\rm RD}(\boldsymbol{u}) = ({\rm RD}(u_1), \cdots, {\rm RD}(u_{300}))$です。

まとめ

　本記事はパラメータの更新式の導出方法についてまとめました。具体的には下記のようになります。

• 前提知識

  • 勾配降下法
    • パラメータを更新式$\beta^{(n+1)} = \beta^{(n)} - \eta \dfrac{\partial L(\beta^{(n)})}{\partial \beta}$で更新する手法です。
    • 勾配$\dfrac{\partial L(\beta^{(n)})}{\partial \beta}$で更新の方向を、学習率$\eta$で更新の大きさを決めます。
  • 合成関数の微分法
    • $y_j = g_j(x_1, x_2, \cdots, x_I), z = f(y_1, \cdots, y_J)$のとき、$\dfrac{\partial z}{\partial x_i} = \displaystyle{\sum_{j=1}^J}\dfrac{\partial y_j}{\partial x_i}\dfrac{\partial z}{\partial y_j}$が成り立つ。

• パラメータの更新式の導出

  • 第1層から第2層のパラメータの勾配
    • 合成関数の微分法を繰り返し適用することで、$\dfrac{\partial L}{\partial W} \propto --\boldsymbol{x}^\top \left\{ (\boldsymbol{y}-\boldsymbol{\hat{y}}) \Theta^\top \odot {\rm RD}(\boldsymbol{u})\right\} $となります。
  • 第2層から第3層のパラメータの勾配
    • 第1層から第2層からの勾配と同様に、合成関数の微分法を適用することで$\dfrac{\partial L(\Theta^{(n)})}{\partial \Theta} \propto -\boldsymbol{z}^\top (\boldsymbol{y}-\boldsymbol{\hat{y}})$となります。

おまけ

　Juliaを使って、パラメータを更新するコードを書きました。必要に応じてコピペして使ってください。

# パッケージの読み込み
using Flux
using Flux.Data: DataLoader
using Flux: onehotbatch, onecold
using Flux.Losses: logitcrossentropy
using MLDatasets

# データセットの読み込み
x_train, y_train = MLDatasets.MNIST.traindata(Float32)
x_test, y_test = MLDatasets.MNIST.testdata(Float32)

# データの可視化
using Plots
heatmap(rotl90(x_train[1:28, 1:28, 1])) # そのままだと横向きに表示されてしまうので、rotl90で行列を右に90度回転させる

# データを(サンプル数×特徴量の個数)に変換する

## 訓練データ
flatten_x_train = transpose(Flux.flatten(x_train)) # 60,000×784
### 60,000枚の画像だと多すぎるので、最初の1,000枚だけを使う
flatten_x_train = flatten_x_train[1:1000, :]

## テストデータ
flatten_x_test = transpose(Flux.flatten(x_test)) # 10,000×784
### 10,000枚の画像だと多すぎるので、最初の1,000枚だけを使う
flatten_x_test = flatten_x_test[1:1000, :]

# one-hot-labelへの変換
## 訓練データ
one_hot_label_y_train =  permutedims(onehotbatch(y_train, 0:9)) # 60,000×10
### 60,000枚の画像だと多すぎるので、最初の1,000枚だけを使う
one_hot_label_y_train = one_hot_label_y_train[1:1000, :]

## テストデータ
one_hot_label_y_test = permutedims(onehotbatch(y_test, 0:9)) # 10,000×10
### 10,000枚の画像だと多すぎるので、最初の1,000枚だけを使う
one_hot_label_y_test = one_hot_label_y_test[1:1000, :]

using LinearAlgebra, Statistics, Random
"""
データ
   訓練データ(特徴量)：flatten_x_train
   訓練データ(目的変数)：one_hot_label_y_train
"""

"""
パラメータ
"""
# 学習率
α = 0.005

# 入力層のサイズ
input_size = size(flatten_x_train)[2] # 784

# 隠れ層のサイズ
hidden_size = 300

# 出力層のサイズ
output_size = 10

W_0_1 = 0.2*rand(input_size, hidden_size).-0.1
W_1_2 = 0.2*rand(hidden_size, output_size).-0.1

# イテレーション
max_iteration = 1

"""
関数
"""
relu(x) = (x>0)*x

relu2deriv(output) = output>0


"""
誤差逆伝播法
"""
# MSEを保存する用のリストを作成
mse_list = []

for iteration=1:max_iteration
   for index=1:size(flatten_x_train)[1]
       # 順伝播
       layer_0 = flatten_x_train[index, :]' # flatten_x_train[index, :]は横ベクトルで値を取得したはずが、縦ベクトルに勝手に変換されてしまう。そのため転置を行っている。
       layer_1_1 = layer_0*W_0_1 # 中間層の活性化関数に入れる前
       layer_1_2 = relu.(layer_1_1) # 中間層の活性化関数に入れた後
       layer_2 = layer_1_2*W_1_2
           
       # 更新式の差分
       ## layer_2のパラメータの更新式の差分
       ### layer_2ではなく、layer_2[1]としているのは、layer2が(1, 1)の行列になっているから
       layer_2_delta = layer_2-one_hot_label_y_train[index, :]'
       W_1_2_delta = α*layer_1_2'*layer_2_delta
       
       ## layer_1のパラメータの更新式の差分
       W_0_1_delta = α*reshape(layer_0, 1, 784)'*(W_1_2*layer_2_delta'.*relu2deriv.(layer_1_1'))'

       # 更新
       W_1_2 = W_1_2-W_1_2_delta        
       W_0_1 = W_0_1-W_0_1_delta
       
   end
   
   # MSE(Mean Square Error)の計算
   ## 全てのデータに対して順伝播を行う
   Layer_1_1 = flatten_x_train*W_0_1 # 中間層の活性化関数に入れる前
   Layer_1_2 = relu.(Layer_1_1) # 中間層の活性化関数に入れた後
   pred_list = Layer_1_2*W_1_2
   

   mse = mean((pred_list-one_hot_label_y_train).^2)
   push!(mse_list, mse)
   println("Error:", mse)
       
end