蟻本3-3「さまざまなデータ構造を操ろう」の区間加算可能なBinary Indexed Treeを行間埋めしました.
問題
数列$A_1,A_2,...,A_N$と$Q$個のクエリが与えられます.クエリを順次処理してください.クエリは次の2種類です.
- $l,r,x$が与えられるので,区間$A_l,A_{l+1},...,A_r$に$x$を加える.
- $l,r$が与えられるので,区間$A_l,A_{l+1},...,A_r$の和を求める.
解法
2つのBinary Indexed Tree(BIT)を用意すると高速に処理することができます.
Binary Indexed Treeとは
以下の記事がわかりやすかったです
BITの特徴をまとめると,
- 1要素$A_i$に$x$を加える操作は高速($O(\log n)$)
- 区間$A_1,A_2,...,A_r$の和算出も高速($O(\log n)$)
- 区間$[l,r]$の和は$\sum_{k=1}^{r}a_k - \sum_{k=1}^{l-1}a_k$で
- ただし,区間$A_l,A_{l+1},...,A_r$に$x$を加える操作は苦手
- BITを2つ組み合わせると高速に処理できる($O(\log n)$)
”区間に値を加える”とは
準備
数列$A_1,A_2,...,A_N$の区間$[l,r]$に$x$を加算した数列を,$A'_1,A'_2,...,A'_N$と書きます.つまり
A'_i =
\begin{cases}
A_i+x & \text{if $ l \le i \lt r+1 $,} \\
A_i & \text{otherwise}.
\end{cases}
また,$s(i),s'(i)$を以下のように定義します.
- $s(i)=\sum_{k=1}^{i}A_k$ (加算前の和)
- $s'(i)=\sum_{k=1}^{i}A'_k$ (加算後の和)
すると,$s(i)$と$s'(i)$の関係は
- $1 \le i \lt l$のとき
$$ s'(i)=s(i) $$ - $l \le i \lt r+1$のとき
$$ s'(i)=s(i)+x(i-l+1) $$ - $r+1 \le i \le N$のとき
$$ s'(i)=s(i)+x(r-l+1) $$
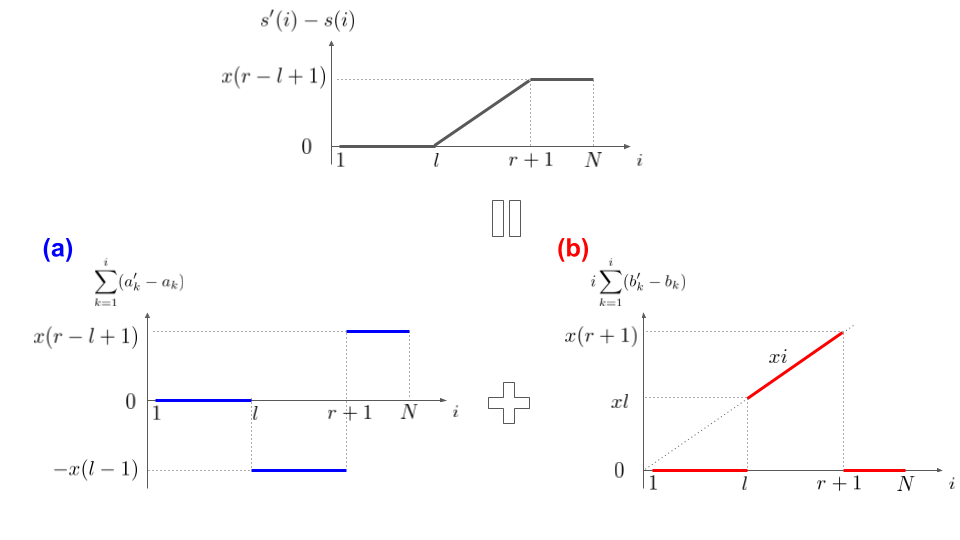
となります.$s(i)$を左辺に移項するとこのようなグラフになります.
このグラフのような$s(i)\rightarrow s'(i)$の更新を高速に行うことが目標です.
2つのBITで和を表す
2つのBIT(BIT0とBIT1とします)を用意して,次のように値を管理するとうまくいきます.
$s(i)$ =(BIT0の1~i要素の和)+ $i$ ×(BIT1の1~i要素の和)
BITは内部で数列の情報を保持し,1要素加算と区間和取得を高速に行うことができるデータ構造でしたので,BIT0,BIT1もそれぞれ内部で数列の情報を保持しています.
BIT0が保持している数列を$a_1,a_2,...,a_N$とします.すなわち
(BIT0の1~i要素の和)= $\sum_{k=1}^{i}a_k$
です.同様にBIT1が保持している数列を数列$b_1,b_2,...,b_N$とおくと,$s(i)$は次のように書けます.
s(i)= \sum_{k=1}^{i}a_k + i \sum_{k=1}^{i}b_k
$s(i)$を更新して$s'(i)$とした後の,BIT0とBIT1の保持している数列をそれぞれ$a'_i,b'_i$と書くと,
s'(i)= \sum_{k=1}^{i}a'_k + i \sum_{k=1}^{i}b'_k
なので
s'(i)-s(i)= \sum_{k=1}^{i}(a'_k-a_k) + i \sum_{k=1}^{i}(b'_k-b_k)
と書けます.
2つのBITの更新方法
「$s'(i)-s(i)$」を2つのBITに割り振ります.
BIT1: $l$から$r$にかけての傾き部分(図の(b))
BIT0: 上記以外(図の(a))
BIT0
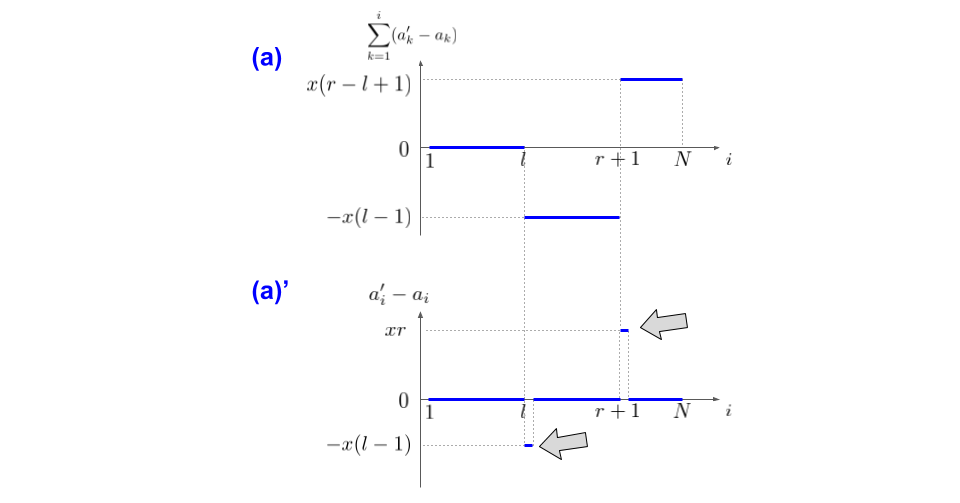
BIT0で管理している数列の和(a)から$\Sigma$を取り除くと(a)'のようになります.
(a)'の$a'_i-a_i$はBIT0で管理している数列$a_i$の更新前後の差なので,これがそのままBIT0への加算量になります.つまり,
- BIT0の$l$個目の要素に$-x(l-1)$を加算
- BIT0の$r+1$個目の要素に$xr$を加算
です.BITの得意な1要素への加算に落とし込むことができました.
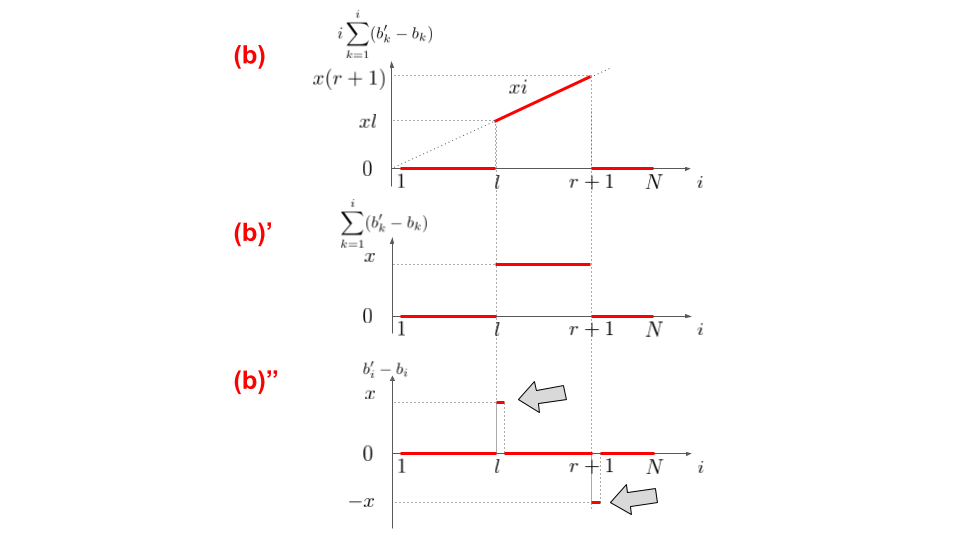
BIT1
BIT1の和には$i$が掛けてあったので,まず$i$を取り除いて(b)'とします.さらに$\Sigma$を取り除くと(b)''になります.
(b)''から,BIT1も次のような1要素への加算に落とし込むことができました.
- BIT1の$l$個目の要素に$x$を加算
- BIT1の$r+1$個目の要素に$-x$を加算
BIT0,BOT1の操作をまとめると
区間$A_l,A_{l+1},...,A_r$に$x$を加える操作は,次の4つの「BITを用いた数列の1要素への加算」で表すことができます.
- BIT0の$l$個目の要素に$-x(l-1)$を加算
- BIT1の$l$個目の要素に$x$を加算
- BIT0の$r+1$個目の要素に$xr$を加算
- BIT1の$r+1$個目の要素に$-x$を加算
和の求め方
数列$A_1,A_2,...,A_N$の$i$要素目までの和は,$s(i)$の定義をそのまま利用して次のように求めます.
$s(i)$ =(BIT0の1~i要素の和)+ $i$ ×(BIT1の1~i要素の和)
実装例
冒頭のリンクの先を参照してください.
終わりに
蟻本は一目見ると説明不足に感じますが,後で読み直すと必要十分な説明になっていますね.