LDAによるトピック解析 with Gensim

はじめに

今回は、Latent Dirichlet Allocation（潜在的ディリクレ配分法、以下「LDA」と略）と呼ばれるトピックモデルについて取り上げます。
特に本記事では、LDA というトピックモデルを扱う上で押さえておくべき、トピックモデルやコーパスの概念に触れながら、前処理を含めた分析の流れやモデルの評価方法などについて、実装を通じて理解を深めていくことを目的とします。
また併せて、本記事では、結果の可視化の手法についてもいくつか紹介したいと思います。
分析の流れとしては、ストップワードなどの文章の前処理の後、Gensim を用いて、文章をいくつかのトピックに分類していき、最後に WordCloud と pyLDAvis により結果の可視化を行っていきます。

目次

• トピックモデルについて
• 分析環境と事前準備
• モジュールの設定とデータのインポート
• 前処理
• 辞書とコーパスの作成
• トピック数の検討とモデリング
• モデルの評価
• 可視化
• 補遺
• 参考情報
• 最後に

トピックモデルについて

実装に入る前に、そもそもトピックモデルとは何かについて、説明したいと思います。

「トピックモデル」とは、データが「潜在的意味のカテゴリ」から生成されると仮定したモデルのことです。
この「潜在的意味のカテゴリ」の事を、「潜在トピック」または単に「トピック」と呼びます。
ここでの「潜在的意味」とは、複数の単語の共起性によって創発される情報のことを指しています。
因みに、なぜ「トピックモデル」の説明の中で「潜在的」という言葉が用いられているのかというと、文書ごとによって共起する単語が異なるため、トピックモデルでは、文書を「意味のカテゴリ」に分ける際に、文書に実際に現れる顕在的共起性だけでなく、文書上には現れない隠れた共起性である潜在的共起性も、同時に扱っているからです。
本記事で取り上げる LDA は、上記で説明したトピックモデルの1つであると同時に、Probabilistic Latent Semantic Indexing（Probabilistic Latent Semantic Analysis（PLSA）とも呼ばれますが、以下では「PLSI」と略）というトピックモデルの拡張モデルでもあります。

ここで、LDA がどのようなモデルなのかを理解するために、PLSI と LDA の違いについても少し触れておきましょう。
PLSI において、あるドキュメントdにおける単語wの共起確率 p(d,w) は、以下の数式のように表すことができます。

\begin{align}
p(d,w) &= p(d)\sum_{z} p(w|z)p(z|d)\\
&= p(d)\sum_{z} p(w|z)\frac{p(d|z)p(z)}{p(d)} \\
&= \sum_{z} p(z)p(w|z)p(d|z)
\end{align}

• p(d)：ドキュメントdの出現しやすさ
• p(w|z)：ドキュメントdに出現する単語wの、トピックzにおける出現のしやすさ
• p(z|d)：ドキュメントdに対してトピックzが生成される確率（トピック分布）
• p(z)：トピックzの存在確率
• p(d|z)：ドキュメントdがトピックzである確率

p(d) は一般的には計算し難いため、上記の式のように、ベイズの定理を用いて p(z|d) を展開し、右辺の p(d) を消して、p(z)・p(w|z)・p(d|z)の3つのパラメータの式に変形します。
PLSI では、学習データの尤度が最大となるような上記3つのパラメータを、EMアルゴリズムによって推定していきます。
この PLSI という手法が開発されたことで、膨大な文書を意味のあるカテゴリに分類することができるようになりました。

ただし、この PLSI には大きく2つの弱点が存在します。
まず1つ目が、トピック分布である p(z|d) は学習データのドキュメント d に直接依存するため、新規のドキュメントに対しては自然に扱うことができません。
そして2つ目が、推定するパラメータの1つである p(d|z) の数は、ドキュメント数×トピック数となるため、ドキュメント数が膨大になると、推定すべきパラメータ数も比例して増大することとなり、その結果、学習データに対しても簡単にオーバーフィットしてしまいます。

こうした PLSI の弱点を克服したモデルが LDA になります。
そもそもトピック分布である p(z|d) が学習データについてのみ定義されていることが、PLSI の問題点であったので、この p(z|d) 自体を確率変数とみて生成することができれば、学習データに依存せず、ドキュメント数に応じてパラメータ数が増大することもなくなります。
LDA では、このトピック分布の確率変数をディリクレ分布を用いて生成することで、PLSI の問題点に対処しています。
LDA の詳細な説明については、長くなるため割愛しますが、ここでは PLSI と LDA の違いが、各モデルで定義されているトピック分布に起因していることが理解できていれば大丈夫です。
LDA は、上記のようにトピック分布を確率変数として生成することで、PLSI の弱点であった新規のドキュメントも自然に扱えるようになっており、オーバーフィットもし難くなっています。
また、LDA は階層ベイズモデルであるため、PLSI と違い、様々な拡張が可能なのも特徴の1つと言えるでしょう。

こうして書くと、LDA の方が PLSI よりも優れているように見えるかもしれませんが、必ずしもそういうわけではありません。
PLSI は尤度最大化をするため、オーバーフィットし易いという一面はありますが、今あるデータに対してアドホック的に分析してみるといった場合においては、PLSI の方に分があります。
一方、扱うドキュメント数が膨大であったり、今後も新規のドキュメントが投入され、モデルを更新し続ける必要がある場合は、LDA の方が適していると言えます。
分析をする際は、このように目的や状況に応じて、より適したモデルを選択することが肝要です。

因みに余談ですが、今回の分析は、手元にあるデータがどのようなトピックに分類されるのかと、分類されたトピックに大きな偏りが生じていないかを確認したいという目的で始めたのですが、扱うテキストデータのドキュメント数が約180万件と多かったことから、オーバーフィットを避けるために、PLSI ではなく LDA を採用したといった経緯があります。

以上で、トピックモデルについての説明を終わりたいと思います。

分析環境と事前準備

本記事における実装では、KaggleのKernelを使用しています。
参考までに、Kaggleの環境のスペック及び設定を、以下に挙げておきます。

• Python 3.6.6
• Anaconda conda 4.6.14
• RAM 16GB
• Disk 4.9GB
• Language Python
• GPU Off
• Internet Off

また、ローカル環境を使用する場合は、以下のコマンドをコマンドプロンプトに打ち込んで、各モジュールをインストールしておきましょう。

pip install gensim
pip install wordcloud 
pip install pyLDAvis

また、今回のLDAで使用するテキストデータですが、Jigsaw Unintended Bias in Toxicity ClassificationというKaggleのコンペティションのデータセットを加工したものを使用します。
テキストデータの加工については、また別の記事で取り上げる予定ですので、興味がある方はそちらをご参照下さい。

モジュールの設定とデータのインポート

上記の準備が終わったら，モジュールのインポートをします。
今回使用するモジュールは以下の通りです。

lda_model.py

# This Python 3 environment comes with many helpful analytics libraries installed
# It is defined by the kaggle/python docker image: https://github.com/kaggle/docker-python
# For example, here's several helpful packages to load in 

import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)

# NLP
import glob
from tqdm import tqdm
import math
import urllib
import gensim
from gensim import corporafrom collections import defaultdict

# pyLDAvis
import pyLDAvis
import pyLDAvis.gensim
pyLDAvis.enable_notebook()

# Vis
from wordcloud import WordCloud
from PIL import Image
import matplotlib
matplotlib.use('Agg') 
import matplotlib.pylab as plt
font = {'family': 'TakaoGothic'}
matplotlib.rc('font', **font)

# Input data files are available in the "../input/" directory.
# For example, running this (by clicking run or pressing Shift+Enter) will list the files in the input directory

import os
import gc
import logging
import pickle
from smart_open import open
print(os.listdir("../input"))

# Any results you write to the current directory are saved as output.

次に、分析で使用するデータをインポートしてきます。
その際に、使用するテキストデータ以外に、別途用意したストップワードのリストもインポートしておきます。

lda_model.py

# importing the dataset
train=pd.read_csv("../input/train_cleaned.csv")

# importing stopwords
f = open('../input/stopwords-en.txt')
stopword = f.read()
f.close()

英語のストップワードのリストは、Kaggleのデータセットでもいくつか公開されています。
詳細については、以下に公開されているデータセットのリンクを記載しておきますので、そちらをご参照下さい。

• Stopwords-En（https://www.kaggle.com/mauropelucchi/stopwordsen）

前処理

ここでは前処理として、シンボルとストップワードを除去してきます。

まず最初に、シンボルの除去を行っていきます。
今回使用するテキストデータでは、「?」や「!」などの記号や、「"」や「'」などの符号に加え、絵文字や顔文字なども多く使用されています。
そこで、以下のコードでは、絵文字や顔文字などのリストをsymbolsとして定義した上で、除去する記号や符号のリストにsymbolsを加える形で対応しています。
一部除去する記号や符号が重複していますが、その点はご容赦いただければと思います。

lda_model.py

# setting symbols
symbols = '.,?!-;*"…:—()%#$&_/@＼・ω+=”“[]^–>\\°<~•≠™ˈʊɒ∞§{}·τα❤☺ɡ|¢→̶`❥━┣┫┗Ｏ►★©―ɪ✔®\x96\x92●£♥➤´¹☕≈÷♡◐║▬′ɔː€۩۞†μ✒➥═☆ˌ◄½ʻπδηλσερνʃ✬ＳＵＰＥＲＩＴ☻±♍µº¾✓◾؟．⬅℅»Вав❣⋅¿¬♫ＣＭβ█▓▒░⇒⭐›¡₂₃❧▰▔◞▀▂▃▄▅▆▇↙γ̄″☹➡«φ⅓„✋：¥̲̅́∙‛◇✏▷❓❗¶˚˙）сиʿ✨。ɑ\x80◕！％¯−flfi₁²ʌ¼⁴⁄₄⌠♭✘╪▶☭✭♪☔☠♂☃☎✈✌✰❆☙○‣⚓年∎ℒ▪▙☏⅛ｃａｓǀ℮¸ｗ‚∼‖ℳ❄←☼⋆ʒ⊂、⅔¨͡๏⚾⚽Φ×θ￦？（℃⏩☮⚠月✊❌⭕▸■⇌☐☑⚡☄ǫ╭∩╮，例＞ʕɐ̣Δ₀✞┈╱╲▏▕┃╰▊▋╯┳┊≥☒↑☝ɹ✅☛♩☞ＡＪＢ◔◡↓♀⬆̱ℏ\x91⠀ˤ╚↺⇤∏✾◦♬³の｜／∵∴√Ω¤☜▲↳▫‿⬇✧ｏｖｍ－２０８＇‰≤∕ˆ⚜☁\n🍕\r🐵😑\xa0\ue014\t\uf818\uf04a\xad😢🐶️\uf0e0😜😎👊\u200b\u200e😁عدويهصقأناخلىبمغر😍💖💵Е👎😀😂\u202a\u202c🔥😄🏻💥ᴍʏʀᴇɴᴅᴏᴀᴋʜᴜʟᴛᴄᴘʙғᴊᴡɢ😋👏שלוםבי😱‼\x81エンジ故障\u2009🚌ᴵ͞🌟😊😳😧🙀😐😕\u200f👍😮😃😘אעכח💩💯⛽🚄🏼ஜ😖ᴠ🚲‐😟😈💪🙏🎯🌹😇💔😡\x7f👌ἐὶήιὲκἀίῃἴξ🙄Ｈ😠\ufeff\u2028😉😤⛺🙂\u3000تحكسة👮💙فزط😏🍾🎉😞\u2008🏾😅😭👻😥😔😓🏽🎆🍻🍽🎶🌺🤔😪\x08‑🐰🐇🐱🙆😨🙃💕𝘊𝘦𝘳𝘢𝘵𝘰𝘤𝘺𝘴𝘪𝘧𝘮𝘣💗💚地獄谷улкнПоАН🐾🐕😆ה🔗🚽歌舞伎🙈😴🏿🤗🇺🇸мυтѕ⤵🏆🎃😩\u200a🌠🐟💫💰💎эпрд\x95🖐🙅⛲🍰🤐👆🙌\u2002💛🙁👀🙊🙉\u2004ˢᵒʳʸᴼᴷᴺʷᵗʰᵉᵘ\x13🚬🤓\ue602😵άοόςέὸתמדףנרךצט😒͝🆕👅👥👄🔄🔤👉👤👶👲🔛🎓\uf0b7\uf04c\x9f\x10成都😣⏺😌🤑🌏😯ех😲Ἰᾶὁ💞🚓🔔📚🏀👐\u202d💤🍇\ue613小土豆🏡❔⁉\u202f👠》कर्मा🇹🇼🌸蔡英文🌞🎲レクサス😛外国人关系Сб💋💀🎄💜🤢َِьыгя不是\x9c\x9d🗑\u2005💃📣👿༼つ༽😰ḷЗз▱ц🤣卖温哥华议会下降你失去所有的钱加拿大坏税骗子🐝ツ🎅\x85🍺آإشء🎵🌎͟ἔ油别克🤡🤥😬🤧й\u2003🚀🤴ʲшчИОРФДЯМюж😝🖑ὐύύ特殊作戦群щ💨圆明园קℐ🏈😺🌍⏏ệ🍔🐮🍁🍆🍑🌮🌯🤦\u200d𝓒𝓲𝓿𝓵안영하세요ЖљКћ🍀😫🤤ῦ我出生在了可以说普通话汉语好极🎼🕺🍸🥂🗽🎇🎊🆘🤠👩🖒🚪天一家⚲\u2006⚭⚆⬭⬯⏖新✀╌🇫🇷🇩🇪🇮🇬🇧😷🇨🇦ХШ🌐\x1f杀鸡给猴看ʁ𝗪𝗵𝗲𝗻𝘆𝗼𝘂𝗿𝗮𝗹𝗶𝘇𝗯𝘁𝗰𝘀𝘅𝗽𝘄𝗱📺ϖ\u2000үսᴦᎥһͺ\u2007հ\u2001ɩｙｅ൦ｌƽｈ𝐓𝐡𝐞𝐫𝐮𝐝𝐚𝐃𝐜𝐩𝐭𝐢𝐨𝐧Ƅᴨןᑯ໐ΤᏧ௦Іᴑ܁𝐬𝐰𝐲𝐛𝐦𝐯𝐑𝐙𝐣𝐇𝐂𝐘𝟎ԜТᗞ౦〔Ꭻ𝐳𝐔𝐱𝟔𝟓𝐅🐋ffi💘💓ё𝘥𝘯𝘶💐🌋🌄🌅𝙬𝙖𝙨𝙤𝙣𝙡𝙮𝙘𝙠𝙚𝙙𝙜𝙧𝙥𝙩𝙪𝙗𝙞𝙝𝙛👺🐷ℋ𝐀𝐥𝐪🚶𝙢Ἱ🤘ͦ💸ج패티Ｗ𝙇ᵻ👂👃ɜ🎫\uf0a7БУі🚢🚂ગુજરાતીῆ🏃𝓬𝓻𝓴𝓮𝓽𝓼☘﴾̯﴿₽\ue807𝑻𝒆𝒍𝒕𝒉𝒓𝒖𝒂𝒏𝒅𝒔𝒎𝒗𝒊👽😙\u200cЛ‒🎾👹⎌🏒⛸公寓养宠物吗🏄🐀🚑🤷操美𝒑𝒚𝒐𝑴🤙🐒欢迎来到阿拉斯ספ𝙫🐈𝒌𝙊𝙭𝙆𝙋𝙍𝘼𝙅ﷻ🦄巨收赢得白鬼愤怒要买额ẽ🚗🐳𝟏𝐟𝟖𝟑𝟕𝒄𝟗𝐠𝙄𝙃👇锟斤拷𝗢𝟳𝟱𝟬⦁マルハニチロ株式社⛷한국어ㄸㅓ니͜ʖ𝘿𝙔₵𝒩ℯ𝒾𝓁𝒶𝓉𝓇𝓊𝓃𝓈𝓅ℴ𝒻𝒽𝓀𝓌𝒸𝓎𝙏ζ𝙟𝘃𝗺𝟮𝟭𝟯𝟲👋🦊多伦🐽🎻🎹⛓🏹🍷🦆为和中友谊祝贺与其想象对法如直接问用自己猜本传教士没积唯认识基督徒曾经让相信耶稣复活死怪他但当们聊些政治题时候战胜因圣把全堂结婚孩恐惧且栗谓这样还♾🎸🤕🤒⛑🎁批判检讨🏝🦁🙋😶쥐스탱트뤼도석유가격인상이경제황을렵게만들지않록잘관리해야합다캐나에서대마초와화약금의품런성분갈때는반드시허된사용🔫👁凸ὰ💲🗯𝙈Ἄ𝒇𝒈𝒘𝒃𝑬𝑶𝕾𝖙𝖗𝖆𝖎𝖌𝖍𝖕𝖊𝖔𝖑𝖉𝖓𝖐𝖜𝖞𝖚𝖇𝕿𝖘𝖄𝖛𝖒𝖋𝖂𝕴𝖟𝖈𝕸👑🚿💡知彼百\uf005𝙀𝒛𝑲𝑳𝑾𝒋𝟒😦𝙒𝘾𝘽🏐𝘩𝘨ὼṑ𝑱𝑹𝑫𝑵𝑪🇰🇵👾ᓇᒧᔭᐃᐧᐦᑳᐨᓃᓂᑲᐸᑭᑎᓀᐣ🐄🎈🔨🐎🤞🐸💟🎰🌝🛳点击查版🍭𝑥𝑦𝑧ＮＧ👣\uf020っ🏉ф💭🎥Ξ🐴👨🤳🦍\x0b🍩𝑯𝒒😗𝟐🏂👳🍗🕉🐲چی𝑮𝗕𝗴🍒ꜥⲣⲏ🐑⏰鉄リ事件ї💊「」\uf203\uf09a\uf222\ue608\uf202\uf099\uf469\ue607\uf410\ue600燻製シ虚偽屁理屈Г𝑩𝑰𝒀𝑺🌤𝗳𝗜𝗙𝗦𝗧🍊ὺἈἡχῖΛ⤏🇳𝒙ψՁմեռայինրւդձ冬至ὀ𝒁🔹🤚🍎𝑷🐂💅𝘬𝘱𝘸𝘷𝘐𝘭𝘓𝘖𝘹𝘲𝘫کΒώ💢ΜΟΝΑΕ🇱♲𝝈↴💒⊘Ȼ🚴🖕🖤🥘📍👈➕🚫🎨🌑🐻𝐎𝐍𝐊𝑭🤖🎎😼🕷ｇｒｎｔｉｄｕｆｂｋ𝟰🇴🇭🇻🇲𝗞𝗭𝗘𝗤👼📉🍟🍦🌈🔭《🐊🐍\uf10aლڡ🐦\U0001f92f\U0001f92a🐡💳ἱ🙇𝗸𝗟𝗠𝗷🥜さようなら🔼'

# deleate symbols
def basic_preprocess(data):
    data = str(data)
    data = data.lower()
    '''
    Credit goes to https://www.kaggle.com/gpreda/jigsaw-fast-compact-solution
    '''
    punct =  "/-'?!.,#$%\'()*+-/:;<=>@[\\]^_`{|}~`" + '""“”’' + '∞θ÷α•à−β∅³π‘₹´°£€\×™√²—–&' + symbols
    def clean_special_chars(text, punct):        
        for p in punct:
            text = text.replace(p, ' ')
        return text

    data = clean_special_chars(data, punct)
    return data

train['cleaned'] = train['comment_text'].apply(basic_preprocess)

次に、ストップワードとして定義した単語を除外していきます。
通常ストップワードとして設定される「and」や「of」に加えて、「good」や「bad」などの形容詞や、「they」や「you」などの代名詞も、ストップワードとして除外していきます。

lda_model.py

#list
all_text = list(train['cleaned'])

# filter stopwords
stop_words = set(stopword.split())
texts = [[word for word in document.lower().split() if word not in stop_words] for document in all_text]

# reduce memory
del train
del all_text
gc.collect()

最後に、今回は後続処理で Bag-of-Words を使用するため、それを考慮して、全文章において、頻出回数が閾値以下となっている単語を除外していきます。
今回の分析では閾値を100回に設定しています。

lda_model.py

# setting frequency
frequency = defaultdict(int)

# count the number of occurrences of the word
for text in texts:
    for token in text:
        frequency[token] += 1

# build only words above 100 into an array
texts = [[token for token in text if frequency[token] > 100] for text in texts]

# save texts
with open("texts.pkl",'wb') as f:
    pickle.dump(texts,f)

辞書とコーパスの作成

前処理が終わったら、LDAのモデリングに必要な辞書とコーパスを用意していきます。

辞書の作成

まず最初に辞書を作っていきます。
文書をベクトルに変換するために、今回の分析では一般的なアプローチ方法である Bag-of-Words（以下では「BoW」と略）というドキュメントの表現方法を使用しています。
この表現方法では、1つのベクトルのそれぞれの要素を、以下のような質問と回答のペアとして表します。

「XXX」という単語が全文書中何回出現したか : XX回

この表現方法のメリットは、質問をそれに対応したIDのみで表せるところにあります。
そして、辞書とはこのIDと質問と回答の組み合わせのことを指しています。
イメージとしては以下の表のようなものになります。

ID	単語	出現回数
11496	abilities	901
139	ability	9085
11628	abject	482
14396	abnormal	222
16124	aboard	384
...	...	...

lda_model.py

# make dictionary
dictionary = corpora.Dictionary(texts)
dictionary.filter_extremes(no_below=3, no_above=0.8)

# vocab size
print('vocab size: ', len(dictionary))

#save dictionary
dictionary.save_as_text("dictionary.txt")

また今回の分析では、以下のコードの箇所で、no_belowとno_aboveの2つの引数を設定し、辞書に登録した単語をフィルタリングしています。
これは、BoW コーパスでは扱い辛い、特定の文書にしか出現しない単語や逆に文書全体で見た時に使用頻度が高い単語を除くことで、LDA の精度の向上が期待できるからです。

dictionary.filter_extremes(no_below=3, no_above=0.8)

各引数の説明は以下の通りです。

• no_below: 出現文書数が閾値以上になるような単語のみを保持します
• no_above: 出現文書数/全文書数が閾値以下になるような単語のみを保持します

因みに、上記2つの引数は、いずれも同一文書内での出現頻度については考慮しません。
今回の分析では、no_below には3、no_above には0.8を設定して、単語のフィルタリングをしています。
また、作成した辞書は dictionary.txt として保存して、後で使用できるようにしておきます。

コーパスの作成

辞書を作成したら、doc2bow() という関数を用いて、トークン化された文書をベクトルに変換します。
doc2bow() は、単純にそれぞれの単語の出現回数を計算した後、単語はIDに変換し、その結果を疎ベクトルとして返します。

lda_model.py

# make corpus
corpus = [dictionary.doc2bow(t) for t in texts]

# save corpus
with open("corpus.pkl",'wb') as f:
    pickle.dump(corpus,f)

結果として以下のようなコーパスが出来上がります。

[(0, 1), (1, 1), (2, 1), (3, 1)]
[(4, 1), (5, 1), (6, 1), (7, 1)]
[(8, 1), (9, 1), (10, 1), (11, 1)]
[(12, 1), (13, 1)]
[(14, 1), (15, 1), (16, 1), (17, 1)]

例えば、疎ベクトル [(12, 1), (13, 1)] の場合では、ある文章中に、ID が12の単語が1回出現し、ID が13の単語が1回出現することを意味しています。

更に、TFIDFオブジェクトを使うことで、「BoW に基づくベクトル表現」を「TFIDF により重み付けを適用したベクトル表現」に変換することもできます。
TFIDF の詳細については割愛しますが、単語の出現頻度だけでなく、文章全体に占める割合も重みとして考慮するモデルであると理解しておけば大丈夫です。

lda_model.py

# tfidf
tfidf = gensim.models.TfidfModel(corpus)
tfidf.save('model.tfidf')

# make corpus_tfidf
corpus_tfidf = tfidf[corpus]

# save corpus_tfidf
with open("corpus_tfidf.pkl",'wb') as f:
    pickle.dump(corpus_tfidf,f)

結果として以下のようなコーパスが出来上がります。
比較の為に、下記のコーパスには、上記の BoW コーパスを TFIDF コーパスに変換したものを載せています。
BoW コーパスと違って疎ベクトルのような形式ではなく、重み付けが考慮された値に変わっていることが分かります。

[(0, 0.6209083565951935), (1, 0.4270908413560687), (2, 0.5445918059283023), (3, 0.3680842170696428)]
[(4, 0.5861878352928633), (5, 0.7063702831821458), (6, 0.27517783370009), (7, 0.28583562519736405)]
[(8, 0.44965682157004144), (9, 0.4952526043816649), (10, 0.48427598026407054), (11, 0.5639240867421602)]
[(12, 0.7007182162460003), (13, 0.7134381412715637)]
[(14, 0.4386145836285086), (15, 0.4064219148658814), (16, 0.6025869780773805), (17, 0.5285143403888968)]

BoW コーパスと TFIDF コーパスの違いは、重み付けをしているかどうかだけなのですが、この重み付けによって、結果の精度も変わってくるので、分析の際の引き出しの1つとして覚えておくと良いでしょう。

トピック数の検討とモデリング

LDA ではトピック数は自動で決まるわけではないので、何個のトピックに分けるのかを分析の際に決めてあげる必要があります。
今回は、モデルの評価指標として一般的に用いられる Perplexity と Coherence を用いて、トピック数を検討していこうと思います。

トピック数の検討に入る前に、ここで Perplexity と Coherence について、簡単に説明したいと思います。

まず、日本語で平均分岐数とも訳される Perplexity について説明します。
Perplexity は汎用能力を表す指標であり、高い精度で予測できるよい確率モデルとも見なされています。
Perplexity を数式で書くと下記のようになります。

\begin{align}
PPL = exp\Biggl\{-\frac{1}{N} \sum_{i=1}^{N} log_2 p(w_i|θ)\Biggr\}
\end{align}

• N：出現単語数
• p($\boldsymbol{w}_i$|θ)：周辺の単語に対するある単語 $\boldsymbol{w}_i$ の発生確率

計算方法としては、学習データとテストデータに分け、モデルに従って学習データでパラメータ θ を求め、未知のテストデータを使って p($\boldsymbol{w}_i$|θ) が最大になるようにパラメータを更新していくという流れになります。
また、上の式では exp を用いていますが、exp は桁数が多すぎると値が飛んでしまうため、代わりに2を用いることもあります。
特徴しては、負の対数尤度であり、また、一般的にトピック数を増やすと共に低くなる傾向にあり、低い程良いとされます。

この Perplexity と共にトピックモデルの評価指標として広く使われているのが、 Coherence になります。
Coherence はトピックの品質を測る指標であり、抽出されたトピックが人間にとって解釈しやすいかどうかを表します。
計算方法としては、学習コーパスより、トピックごとの単語間類似度の平均を対数条件付き確率により求めていく流れであり、トピック全体の Coherence が高ければ、良いモデルと見做します。
今回 Gensim で実装している $\boldsymbol{C}_V$ と呼ばれる Coherence の最適化アルゴリズムは、Röder, Both, Hinneburg (2015) "Exploring the Space of Topic Coherence Measures" が基になっているので、$\boldsymbol{C}_V$ の計算ロジックや他の Coherence の最適化アルゴリズムとの比較などに興味がある方は、そちらの論文も読んでみても良いかもしれません。

Perplexity と Coherence の説明はここまでにして、ここから実際に2つの評価指標を計算し、トピック数を増やしながら、各指標の変遷を確認していきたいと思います。

lda_model.py

#Metrics for Topic Models
start = 2
limit = 22
step = 1

coherence_vals = []
perplexity_vals = []

for n_topic in tqdm(range(start, limit, step)):
    lda_model = gensim.models.ldamodel.LdaModel(corpus=corpus, id2word=dictionary, num_topics=n_topic, random_state=0)
    perplexity_vals.append(np.exp2(-lda_model.log_perplexity(corpus)))
    coherence_model_lda = gensim.models.CoherenceModel(model=lda_model, texts=texts, dictionary=dictionary, coherence='c_v')
    coherence_vals.append(coherence_model_lda.get_coherence())

今回はトピック数が2個からスタートして、1個ずつトピック数を増やしながら、トピック数が21個になるまで、モデルの学習と指標の計算を繰り返していきます。
計算が完了したら、各トピック数ごとのモデルの Perplexity と Coherence の値を折れ線で表示し、それぞれの変遷を確認します。

lda_model.py

# evaluation
x = range(start, limit, step)

fig, ax1 = plt.subplots(figsize=(12,5))

# coherence
c1 = 'darkturquoise'
ax1.plot(x, coherence_vals, 'o-', color=c1)
ax1.set_xlabel('Num Topics')
ax1.set_ylabel('Coherence', color=c1); ax1.tick_params('y', colors=c1)

# perplexity
c2 = 'slategray'
ax2 = ax1.twinx()
ax2.plot(x, perplexity_vals, 'o-', color=c2)
ax2.set_ylabel('Perplexity', color=c2); ax2.tick_params('y', colors=c2)

# Vis
ax1.set_xticks(x)
fig.tight_layout()
plt.show()

# save as png
plt.savefig('metrics.png') 

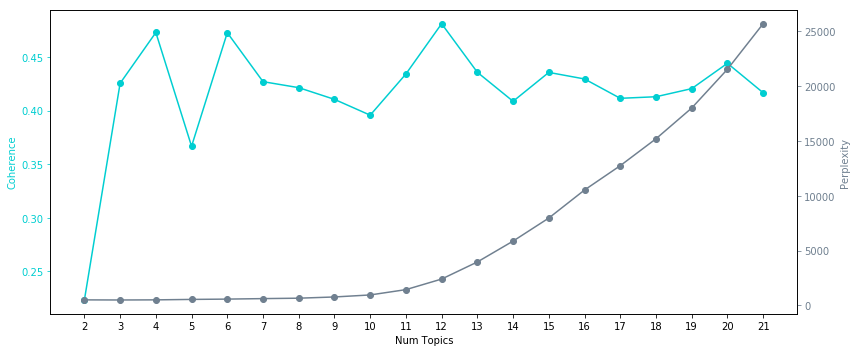
BoW コーパスで学習を行った結果、Perplexity と Coherence は以下のようになりました。

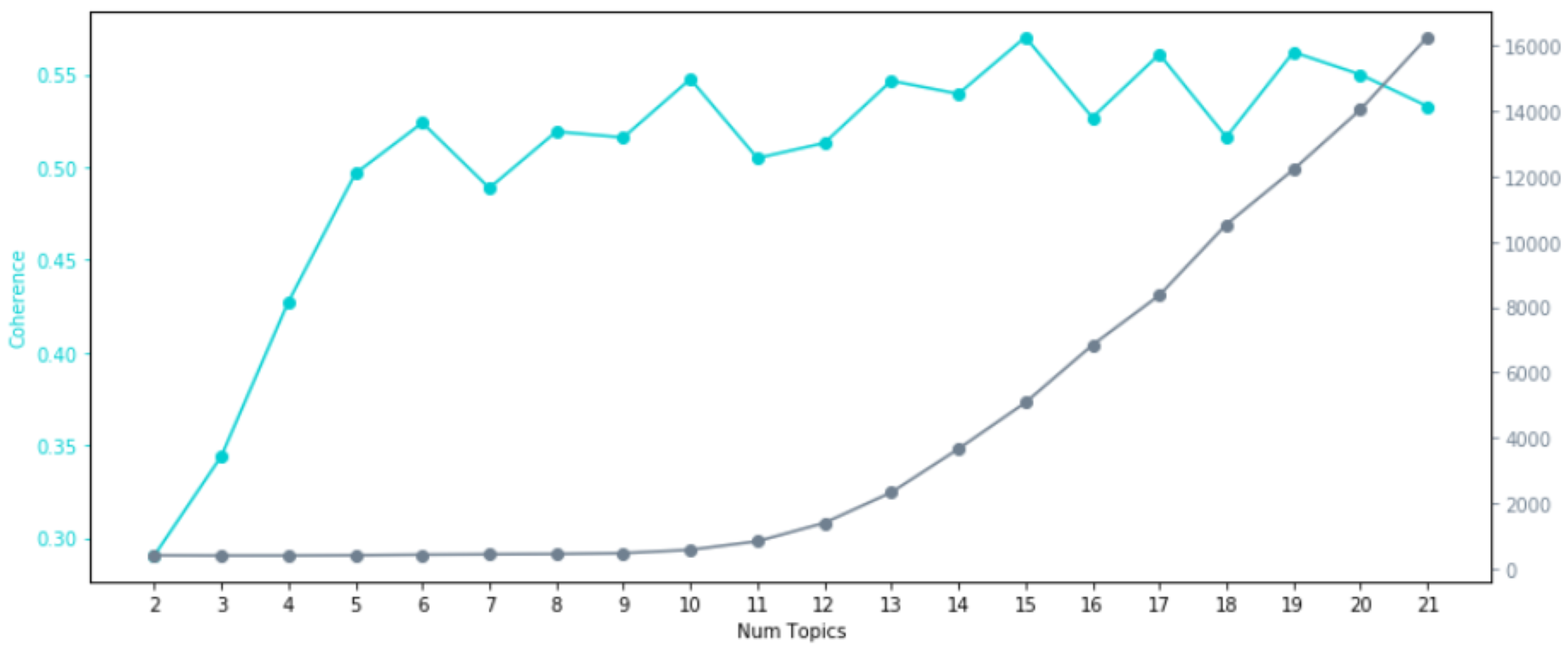
TFIDF コーパスについても、BoWと同様に学習を行い、Perplexity と Coherence を求めました。
結果は以下のようになっています。
BoW コーパスでの学習結果と比べて、Perplexity と Coherence の値や推移が違っているのが良く分かります。

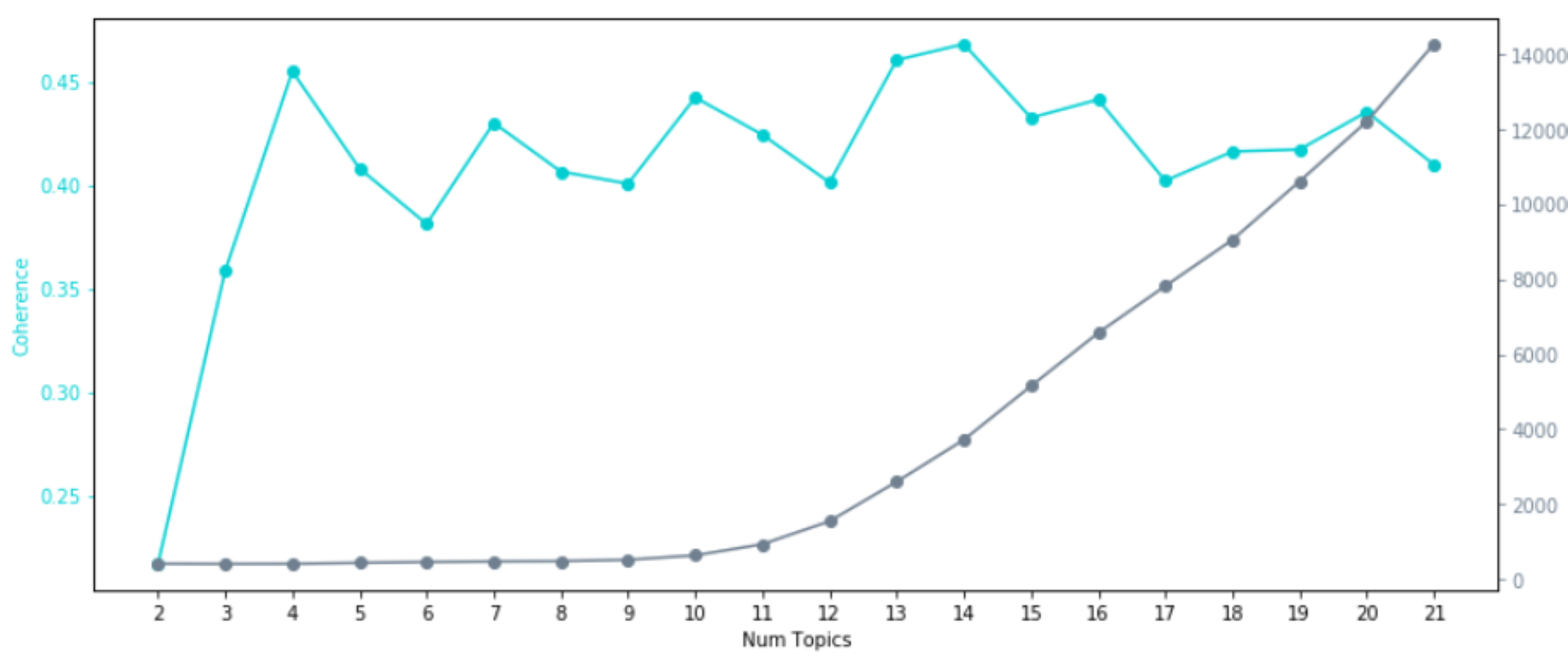
Perplexity は低ければ低い程，Coherence は高ければ高い程、良いモデルであると考えられます。
今回のデータについては、BoW コーパスを使用した場合でも、TFIDF コーパスを使用した場合でも、トピック数としては10個に設定してあげると具合が良さそうです。
比較の意味も込めて、2つのコーパスを使って、トピック数を10個に設定してモデルの学習をしていきます。

lda_model.py

# LDA Model
logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO)
lda_model = gensim.models.ldamodel.LdaModel(corpus=corpus, id2word=dictionary, num_topics=10, alpha=’symmetric’, random_state=0)

# save model
lda_model.save('lda.model')

上記のコードにおいて、alpha=’symmetric’で学習率を設定しており、今回はデフォルトの設定である 1/num_topics を採用しています。
この alpha には、symmetric の他に、asymmetric や auto などが用意されており、更に0.01など直接数値を設定することも可能です。
また、上記のコードでは、random_state=0のところで乱数の設定もしています。
今回の分析では、複数回実行したときの結果の再現性を高めるために、値を0に設定しています。
学習が終わったら、後でモデルが使えるように、学習したモデルの保存もしておきます。
TFIDF コーパスを使用する場合は、上記のコードを次のように書き換えて下さい。
gensim.models.ldamodel.LdaModel(corpus=corpus_tfidf, id2word=dictionary, num_topics=10, alpha='symmetric', random_state=0)

これでモデルの学習が完了しました。

モデルの評価

ここで実際に学習したモデルについて、実際のテストデータを使って、モデルの評価をしてみたいと思います。
今回は出現単語数と Perplexity を比較して、上記で作成したモデルにおいて、出現単語数中正解の選択肢となり得る単語の数がいくらになるかを見ていきます。
実装したものが以下のコードとなっています。

lda_model.py

# importing the dataset
test=pd.read_csv("../input/test_cleaned.csv")

# list
all_text = list(test['comment_text'])

# filter stopwords
test_texts = [[word for word in document.lower().split() if word not in stop_words] for document in all_text]

# make test_corpus
test_corpus = [dictionary.doc2bow(t) for t in test_texts]

# reduce memory
del test
del all_text
gc.collect()

# test
N = sum(count for doc in test_corpus for id, count in doc)
print("N: ",N)

perplexity = np.exp2(-lda_model.log_perplexity(test_corpus))
print("perplexity:", perplexity)

結果は以下のようになりました。

N:  1787627
perplexity: 519.8914706511429

出現単語数が約180万であるのに対して、Perplexity は約520と非常に小さな値を取っているので、良いモデルであることが確認できます。

可視化

本記事では、LDAの結果の可視化の方法として、WordCloud と pyLDAvis という2つのライブラリを使用した方法をご紹介します。

Word Cloud

WordCloud は、テキストデータを頻度の高い単語ほど大きな文字で表示した単語頻度図を生成するライブラリで、LDA の可視化の手法としても良く使われます。
自然言語処理において、対象とする文章中の単語頻度を調べることはとても重要なので、WordCloud による単語頻度図は、それらの直感的な理解の際にとても役立ちます。
また、その見た目から、データサイエンス感を出すのにも向いています(笑)

今回は以下のコードで、トピックごとに単語頻度図を作っていきます。

lda_model.py

# WordCloud
fig, axs = plt.subplots(ncols=2, nrows=math.ceil(lda_model.num_topics/2), figsize=(16,20))
axs = axs.flatten()

def color_func(word, font_size, position, orientation, random_state, font_path):
    return 'darkturquoise'

for i, t in enumerate(range(lda_model.num_topics)):

    x = dict(lda_model.show_topic(t, 30))
    im = WordCloud(
        background_color='black',
        color_func=color_func,
        max_words=4000,
        width=300, height=300,
        random_state=0
    ).generate_from_frequencies(x)
    axs[i].imshow(im.recolor(colormap= 'Paired_r' , random_state=244), alpha=0.98)
    axs[i].axis('off')
    axs[i].set_title('Topic '+str(t))

# vis
plt.tight_layout()
plt.show()

# save as png
plt.savefig('wordcloud.png') 

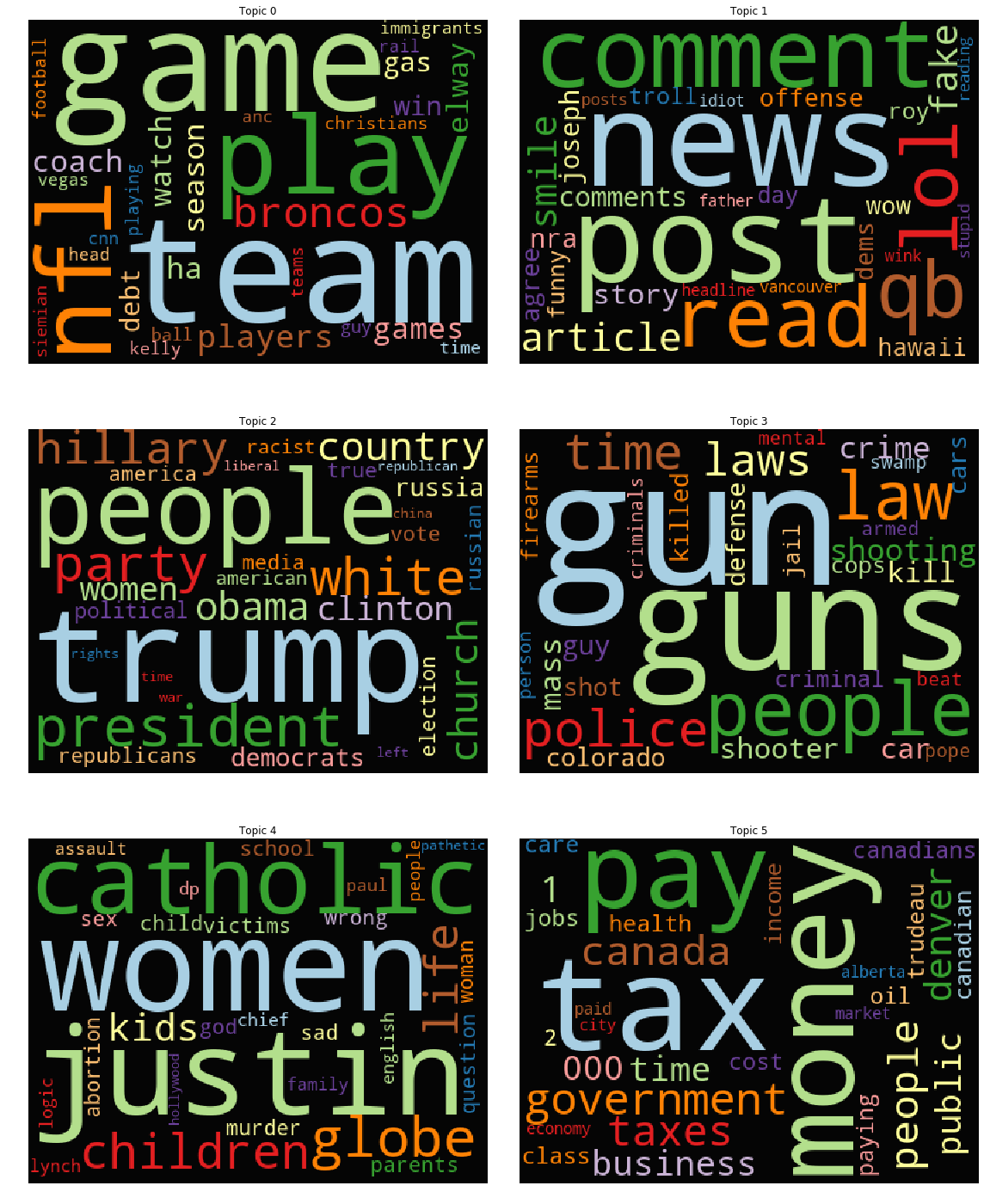
今回はBoWとTFIDFの2つのコーパスでのLDAの結果を、WordCloudで可視化しました。
結果は以下の通りです。

BoW

TFIDF

結果を比べてみると、同じようなトピックがありつつも、BoW コーパスの方では Topic 6のような数字のトピックがある一方で、TFIDFコーパスのモデルでは見られなかったりと、違いがあることが分かります。
また、人間の目で見た場合の解釈性を考えてみると、BoW コーパスを使った LDA の方が、TFIDF コーパスを使ったモデルよりも良さそうな気がします。
ただし、この結果について少し補足すると、上記のモデルで使用した TFIDF コーパスを作成する際に、前処理では BoW コーパス用の処理を行っているため、TFIDF の本来の強みである特定のドキュメントにしか出てこない単語や、ドキュメント内で繰り返し用いられている単語に対する重み付けを上手く活かすことができず、結果的に解釈性が落ちてしまったとも考えられます。
こちらについては、後述の補遺で、TFIDF コーパスの良さが活かせるように前処理を修正した上で、トピック数の検討とモデリングを行った結果を記載しているので、そちらも参考にして下さい。

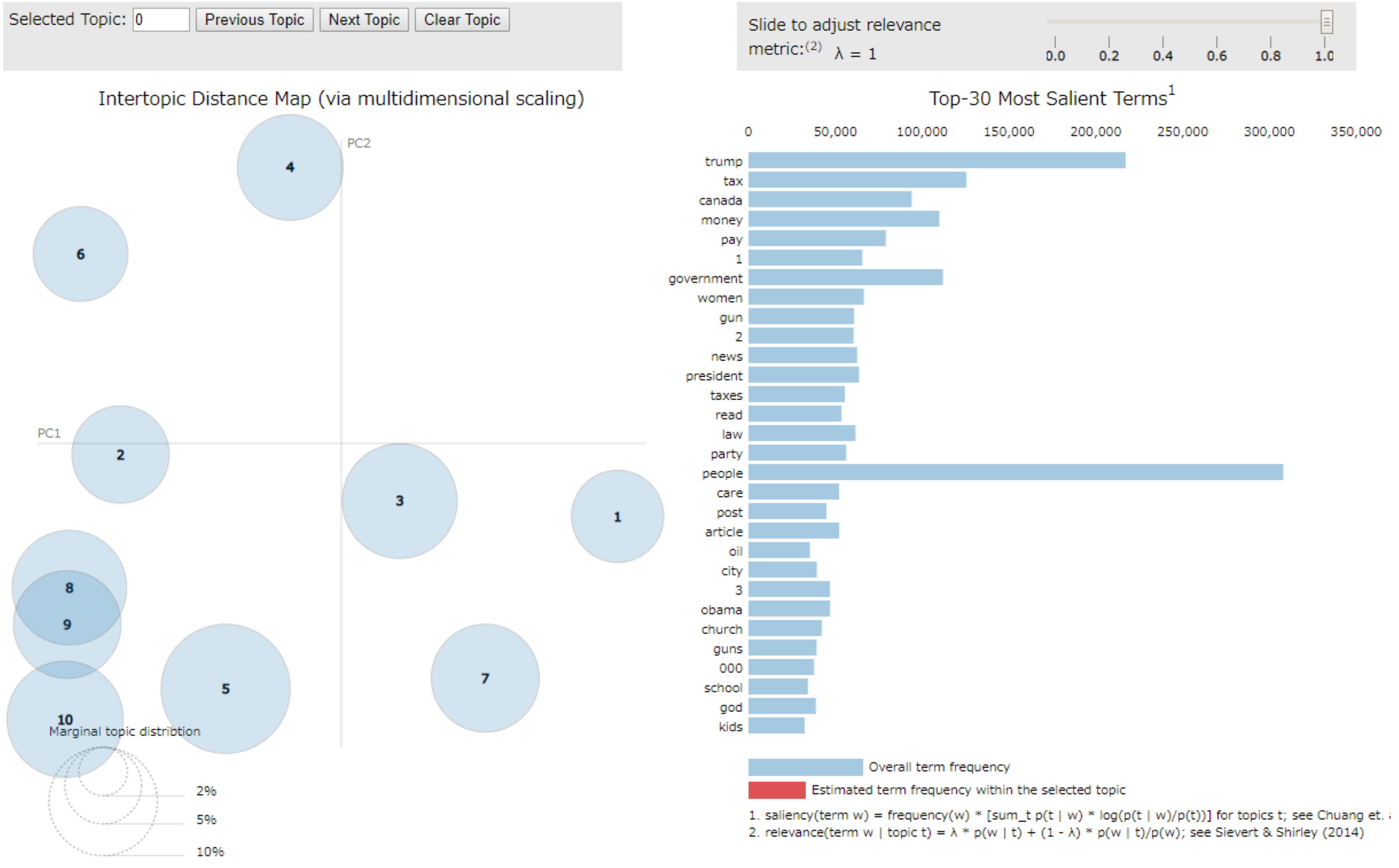
pyLDAvis

pyLDAvisは、LDAの結果をインタラクティブに可視化するためのライブラリです。

pyLDAvisにより生成されるビジュアルについて、簡単に見方を説明します。
まず、左側には各トピックを各多次元尺度法(MDS)で2次元に落として配置したものが表示されます。
この配置された円の大きさは、各トピックに所属するドキュメントの合計を表しており、円と円の距離はトピック間の距離を表しています。
また、右側には選択したトピックの頻出単語、同トピック内での出現頻度が大きい単語とその頻度が表示されます。
右下に説明がありますが、パラメータ λ を変えると出現頻度、同トピック内での出現頻度の割合の比率を変えて順位を変えられます。
更に、右側の単語にマウスを重ねると、各トピック内における出現頻度が左側の円の大きさとして表示されます。

以下の実装では、PCoA、MMDS、t-SNEの3つの多次元尺度法により、結果を可視化しています。

PCoA（Principal Coordinate Analysis）

PCoAは別名、主座標分析とも呼ばれ、古典的MDSに該当する次元削減の手法です。
主座標分析において、低次元に落とす際に使用する距離をユークリッド距離とした場合は、主成分分析と等価になります。
主座標分析が主成分分析と異なっている点は、ユークリッド距離だけでなく、マハラノビス汎距離などの他の距離や、相関係数などの類似度も使えるという点です。

lda_model.py

# Vis PCoA
vis_pcoa = pyLDAvis.gensim_models.prepare(lda_model, corpus, dictionary, sort_topics=False)
vis_pcoa

# save as html
pyLDAvis.save_html(vis_pcoa, 'pyldavis_output_pcoa.html')

結果のビジュアルは以下のようになります。

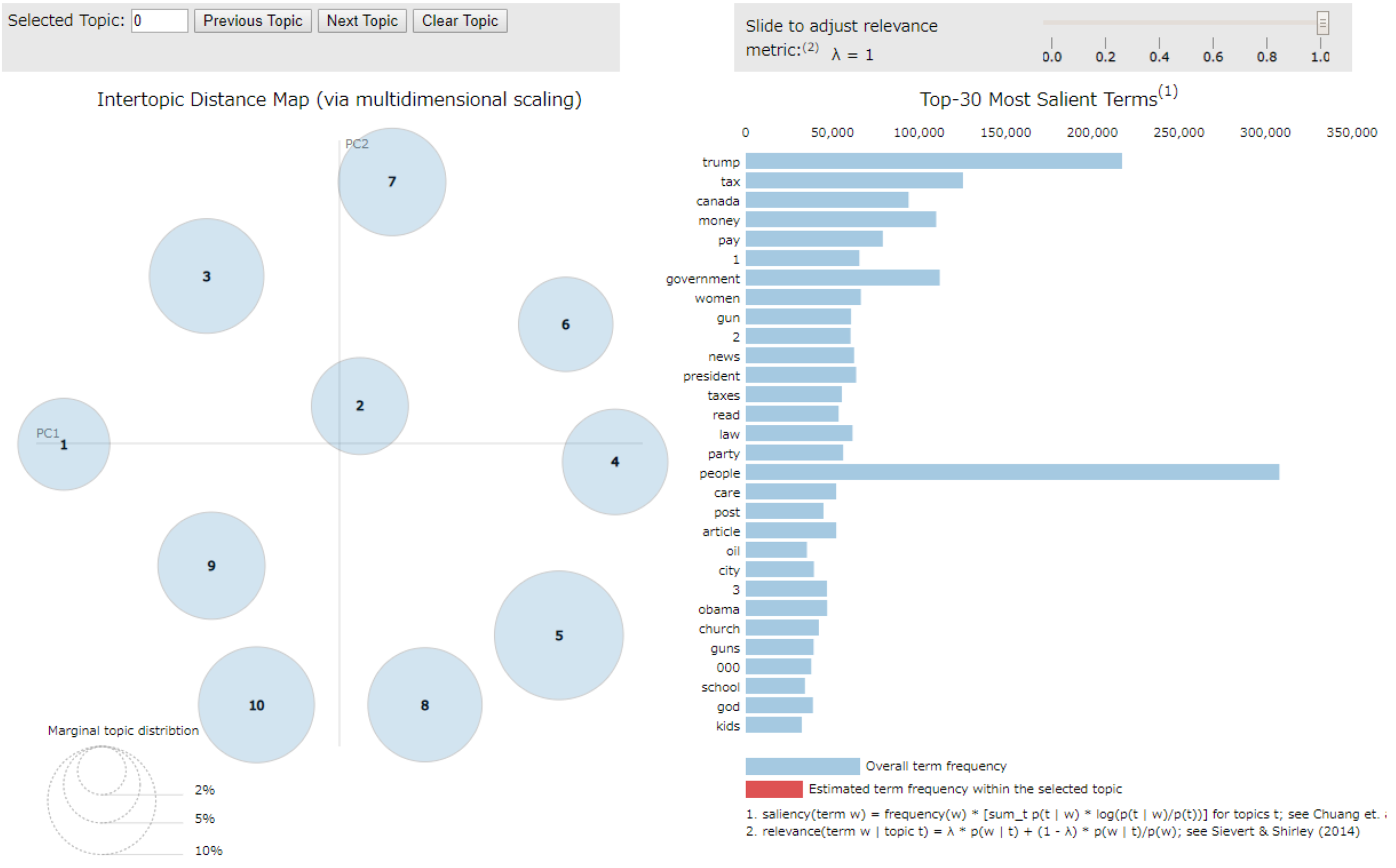
MMDS（Metric Multi-dimensional Scaling）

MMDS は、古典的 MDS の上位集合（superset）であり、計量 MDS と言われたりします。
温度や身長、長さといった比例尺度や間隔尺度等の、定量的数値データを対象に、個体の類似度を計算し、最適な配置を算出するものなので、より厳密な距離関係に向いていると言えます。

lda_model.py

# Vis Metric MDS
vis_mds = pyLDAvis.gensim_models.prepare(lda_model, corpus, dictionary, mds='mmds', sort_topics=False)
vis_mds

# save as html
pyLDAvis.save_html(vis_mds, 'pyldavis_output_mds.html')

結果は以下のようになります。

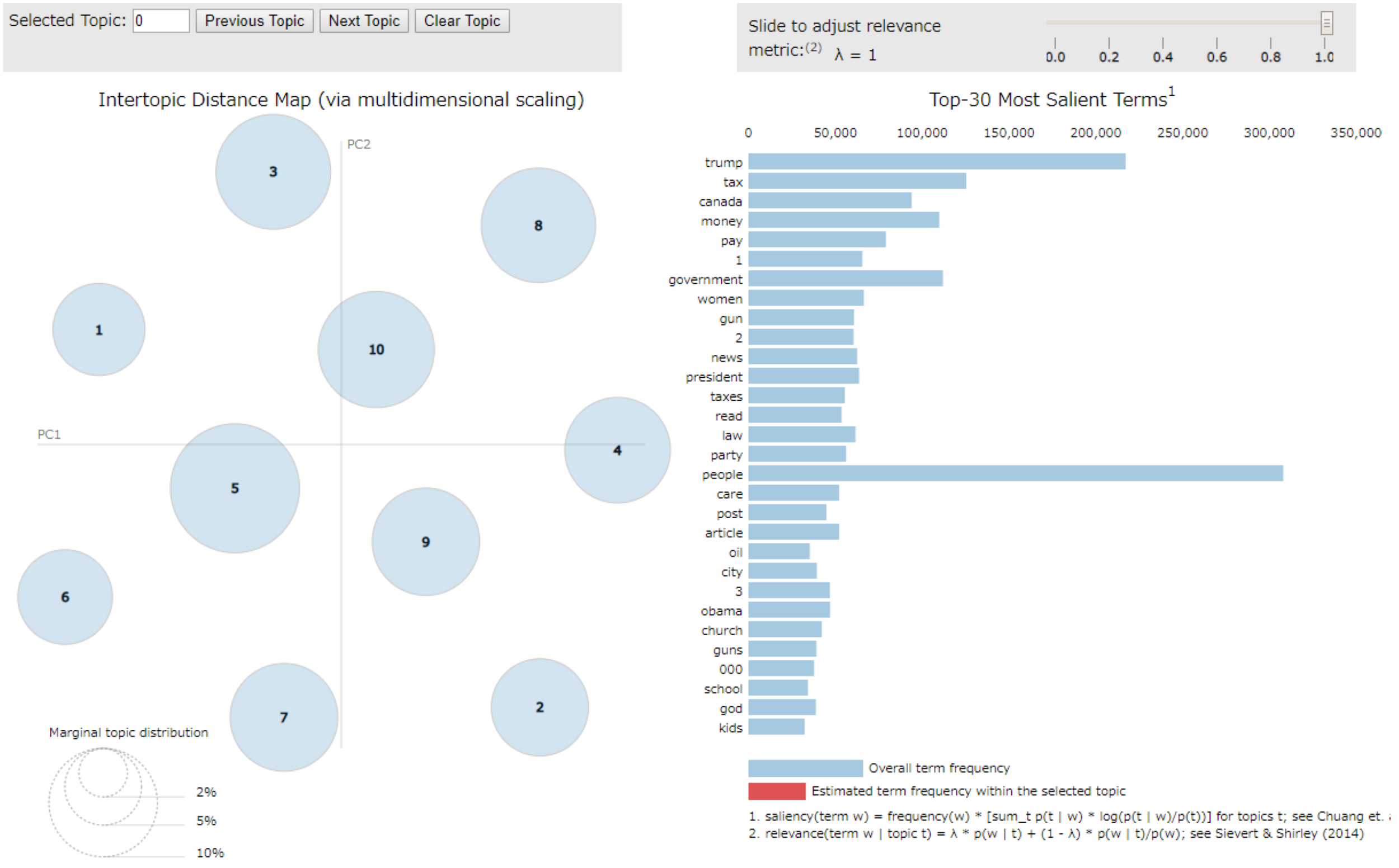
t-SNE（t-distributed Stochastic Neighbor Embedding）

t-SNEは別名、t 分布型確率的近傍埋め込みとも呼ばれる手法で、高次元のデータの可視化に適した次元削減アルゴリズムです。
アルゴリズムの特徴としては、データ同士の「近さ」を、ユークリッド距離やコサイン類似度などではなく、確率分布によって表現することが挙げられます。
ただし、以下のような弱点もあるので、使用する際は注意が必要です。

• 上手くいくことが保証されているのは、2次元，もしくは3次元への圧縮のみです
• 局所構造が次元の呪いの影響を受けやすくなります
• 最適化アルゴリズムの収束性が保証されません

lda_model.py

# Vis t-SNE
vis_tsne = pyLDAvis.gensim_models.prepare(lda_model, corpus, dictionary, mds='tsne', sort_topics=False)
vis_tsne

# save as html
pyLDAvis.save_html(vis_tsne, 'pyldavis_output_tsne.html')

結果は以下の通りです。

使用する次元削減アルゴリズムが変われば、当然ビジュアライズの結果も変わるので、その時々のデータに適した表現方法を選択できれば良いかと思います。

因みに余談ですが、こうした高次元データの構造を解明する方法の一つとして、「トポロジカルデータアナリシス（TDA）」という分野を用いる方法があるそうです。

補遺

上記で実施した分析では、前処理や辞書の作成といった箇所で、BoW を意識した処理をしたため、TFIDF コーパスの強みを活かすことができませんでした。
そこで、補遺という形にはなりますが、ここでTFIDF コーパスを使用するという前提の元、処理を一部修正した上で、TFIDF コーパスを利用した LDA のモデリングを行い、結果がどのように変わるかを確認したいと思います。

まず、前処理の部分については、頻出回数が閾値以下の単語を除外する処理のコードを以下のように修正します。
頻出回数の閾値を100から9に修正することで、10回以上頻出している単語を残すようにしています。

texts = [[token for token in text if frequency[token] > 9] for text in texts]

続いて、辞書の作成のところのフィルタリングのコードを、以下のように修正します。
no_below の設定を削除することで、上記の分析では除外していた出現文書数が3未満の単語も保持しています。

dictionary.filter_extremes(no_above=0.8)

修正は以上となります。

それでは、先程と同じくトピック数の検討をしていきたいと思います。
学習を行った結果、各トピック数における Perplexity と Coherence は以下のようになりました。

上述のものと比べて、計算結果が全く異なっていることが分かります。
特に前回実施した際は、トピック数が6個の時に Coherence の値が比較的に低くなっていたのが、今回の場合では逆に比較的高い値を示しています。
今回の Perplexity と Coherence の結果を見ると、トピック数を6個で設定してあげると良さそうです。

では、トピック数を6個に設定してモデリングを行い、結果を WordCloud で確認してみましょう。
結果は以下のようになりました。
※上記の分析から、各イメージの幅を300から400に変更して、可視化しています。

同じ TFIDF コーパスを使用した前述の分析結果と比べて、いずれのトピックにおいてもどのような内容なのかがはっきりしており、解釈性が飛躍的に向上してるように見えます。

本記事では、TFIDF コーパスを2パターン作成し、それぞれを利用したモデリングの結果を比較することで、辞書やコーパスの前処理の度合いによって、結果の精度も大きく変わることが確認できました。
モデリングした結果、上手くトピックに分けられない場合は、このように前処理を見直し、各コーパスの特徴が活かせるように工夫してみると良いかもしれません。

参考情報

今回記事を書くに当り、参考になった書籍やサイトなどを紹介します。

書籍ですが、私のように理系出身ではない人は勿論、自然言語処理について基礎から学びたい方は、入門書として以下の3冊をオススメします。

• 高村大也 (2010) 『言語処理のための機械学習入門』 株式会社 コロナ社
• 佐藤一誠 (2015) 『トピックモデルによる統計的潜在意味解析』 株式会社 コロナ社
• 黒橋禎夫 (2015) 『自然言語処理』 一般財団法人 放送大学教育振興会

それから、実装の際に参考になったサイトも以下に挙げておきます。

機械学習 潜在意味解析 理論編：
PLSIとLDAについて分かりやすく説明されています。

gensimのDictionaryの中身を簡単にまとめてみた：
gensimのDictionaryについて、各関数とその引数がまとめられています。

WordCloudとpyLDAvisによるLDAの可視化について：
日本語のテキストデータでLDAを実施する際に、どのような流れで分析すれば良いかの参考になります。

tfidf、LSI、LDAの違いについて調べてみた：
BoWやTFIDFといったコーパスの違いについて説明されています。

machine_learning_python/topic.md：
Gensim で LDA を実装する際の学習率の話や、トピック空間での類似度の比較などが説明されています。

LDAとそれでニュース記事レコメンドを作った。：
実装だけでなく、LDAについても数式を交えながら非常に丁寧に解説されています。

深層学習による自然言語処理 - RNN, LSTM, ニューラル機械翻訳の理論 ：
ブログの中で、Perplexityについて、尤度、対数尤度、エントロピーにも触れながら、丁寧に説明されています。

gensimのLDA評価指標coherenceの使い方：
評価指標である Coherence と gensim で実装できる Coherence の計算手法について取り上げられています。

最後に

トピックモデル については、今回勉強するまでほとんど知らなかったのですが、いざ LDA について調べてみると、色々なことに話題が広がっていき、当初の想定を上回る超大作になってしまいました（笑）
勉強会でこの記事を使って発表した際、「もっとこういったことも知りたい」といった意見もいただいたので、それらも可能な限り盛り込みました。
まだまだ勉強中であり、もしかしたら記事の中で間違っていることを書いているかもしれませんが、その時はそっと教えていただけますと幸いです。
他にも記事にしたいネタはたくさんあるので、引き続き頑張って投稿していきたいと思います。

この記事を読んで下さいました皆さんに感謝！！！