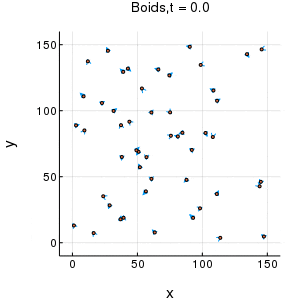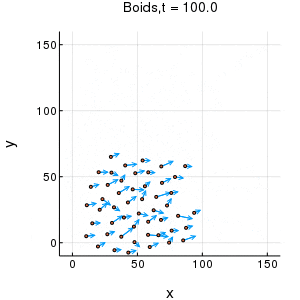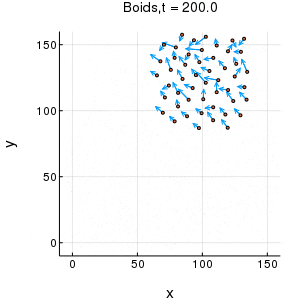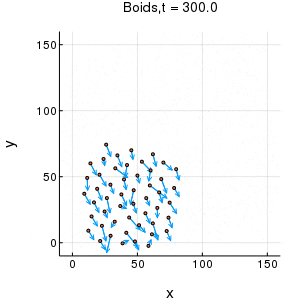
概説
julia言語で簡易的なBoidsシミュレーションを行いました。
はじめに
Boidsとは
Boid(s)とは、"bird(鳥)"+"-oid(~のようなもの)"の造語であり、飛行する鳥の群れをシミュレートするモデルです。人工生命研究者であるCraig Reynoldsが考案しました。このモデルでは、boid1匹1匹がたった3つの相互作用ルールに従って飛行しているだけにもかかわらず、boidの群れ(boids)はあたかも高度な知性を持った1つの生き物のような挙動を示します。その3つのルールを以下に示します。
- Collision Avoidance: 群れの仲間との衝突を避ける
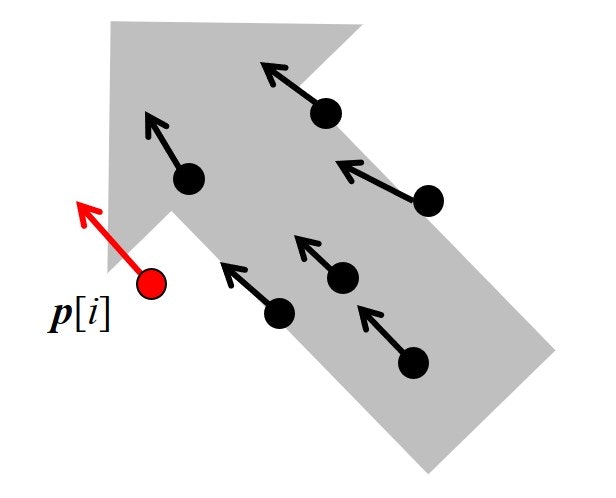
- Velocity Matching: 群れの仲間と速度を合わせようとする
- Flock Centering: 群れの仲間と近づいたままでいようとする
それぞれのルールについて詳しく見ていきます。
定義
$xy$平面に$N$匹のboidが存在します。Boidは位置ベクトル$\boldsymbol{p}$と速度ベクトル$\boldsymbol{v}$をそれぞれ持っています(初期値はランダムです)。$i$番目のboidの位置ベクトルと速度ベクトルを各々$\boldsymbol{p}[i]$,$\boldsymbol{v}[i]$と表します。
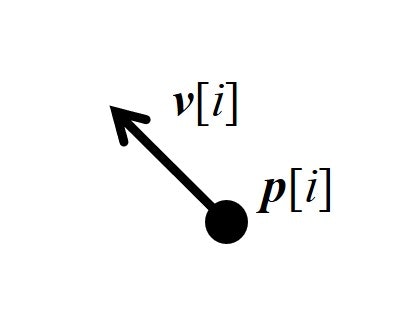
$i$番目のboidに対してルール1-3に基づいて計算して得られた変化量をそれぞれ$\boldsymbol{v_1}[i]$,$\boldsymbol{v_2}[i]$,$\boldsymbol{v_3}[i]$とおきます。現在の速度$\boldsymbol{v}[i]$に$\omega_1 \boldsymbol{v_1}[i]+\omega_2\boldsymbol{v_2}[i]+\omega_3\boldsymbol{v_3}[i]$を加算します($\omega_1$,$\omega_2$,$\omega_3$は重みパラメータ)。
ルール1 Collision Avoidance
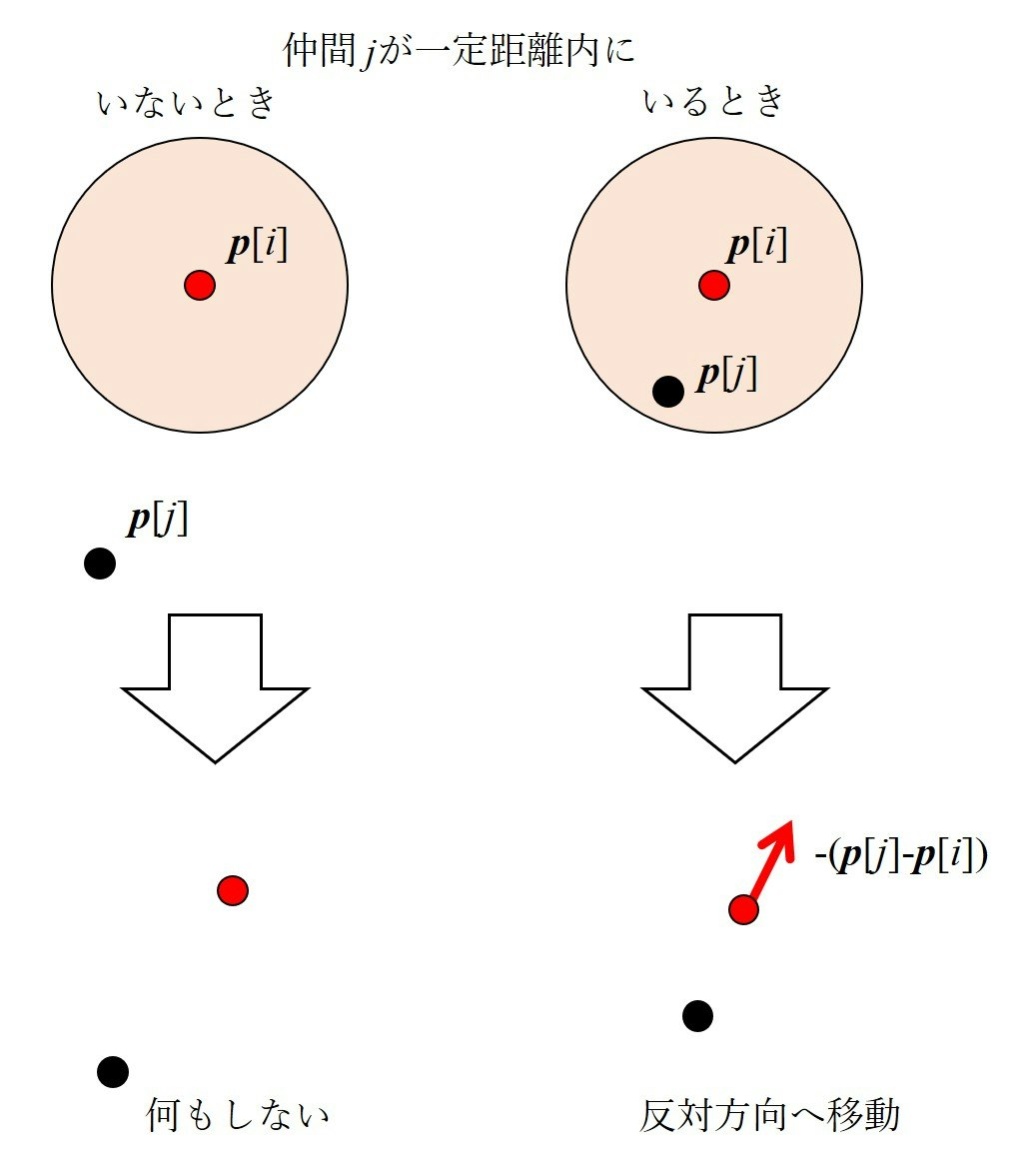
Boidは仲間に近づきすぎたときに衝突を回避しようとします。$i$番目のboidから見て一定の距離内に仲間($j$番目のboid)がいるとき、仲間$j$がいる方向と反対方向に移動しようとします。一定の距離内に複数の仲間がいる場合は合成されたベクトルに従って移動します。
function rule1(param,var)
for i in 1:param.N
for j in 1:param.N
if i==j;continue;end
dist=norm(var.p[j,:].-var.p[i,:])
#ある仲間jとの距離が一定の距離より短ければ
if dist < param.distThresh
var.v1[i,:].-=(var.p[j,:].-var.p[i,:])
end
end
end
end
ルール2 Velocity Matching
Boidは自身の速度を群れ全体の速度に合わせようとします。$i$番目のboidにおけるルール2の計算結果$\boldsymbol{v_2}[i]$は、群れ全体(自身を除く)の平均速度と自身の速度との差です。
\frac{\sum_{i\neq j}^{N} \boldsymbol{v}[j]}{N-1}-\boldsymbol{v}[i]=\boldsymbol{v_2}[i]
function rule2(param,var)
for i in 1:param.N
for j in 1:param.N
if i==j;continue;end
var.v2[i,:].+=var.v[j,:]
end
end
var.v2.=var.v2./(param.N-1)
var.v2.=var.v2.-var.v
end
ルール3 Flock Centering
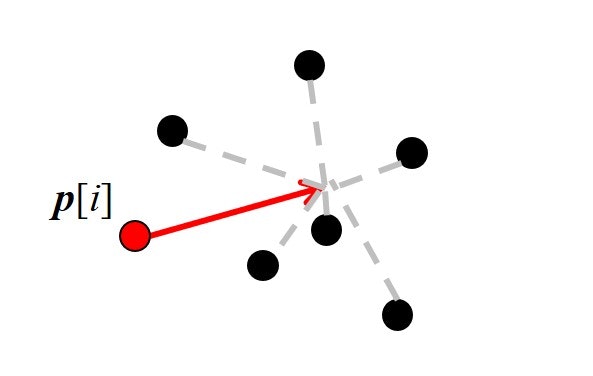
Boidは群れの中心に向かおうとします。$i$番目のboidにおけるルール3の計算結果$\boldsymbol{v_3}[i]$は、群れ全体(自身を除く)の中心位置と自身の位置との差です。
\frac{\sum_{i\neq j}^{N} \boldsymbol{p}[j]}{N-1}-\boldsymbol{p}[i]=\boldsymbol{v_3}[i]
function rule3(param,var)
for i in 1:param.N
for j in 1:param.N
if i==j;continue;end
var.v3[i,:].+=var.p[j,:]
end
end
var.v3.=var.v3./(param.N-1)
var.v3.=var.v3.-var.p
end
付加事項
boidをより本物らしくするためにいくつかの処理を追加します。これらは必須ではありません。
速度制限
本物の鳥は生き物ですから飛行速度には限界があります。また飛行速度がゼロになってしまうのも群れの移動という観点からはあまりうれしくありません。そこでboidの最高速度と最低速度を決めておき、boidの速度がその速度範囲を超えた場合は範囲内に収まるように変化させます。単純なclamp(速度)だと速度がガクンと変わって不自然なので現在速度とclampした値の比をかけて連続的に変化するようにします。
境界判定
世界の大きさの最小値と最大値を決めておきます。Boidの現在位置が世界の外側であり速度方向が世界の外側をむいているとき、速度方向が反対になるようにします。
計算
using Plots
using LinearAlgebra
using Random
Random.seed!(2018)
gr(size=(300,300),titlefont=font("sans-serif",9))
module Boids
struct Param
d::Int64 #次元
N::Int64 #Boidの数
distThresh::Float64 #ルール1の閾値
maxSpeed::Float64 #速度の最大値
minSpeed::Float64 #速度の最小値
maxWorld::Float64 #世界の最大値
minWorld::Float64 #世界の最小値
#R::Float64
ω1::Float64 #rule1の重み
ω2::Float64 #rule2の重み
ω3::Float64 #rule3の重み
end
mutable struct Variables
p::Array{Float64,2} #Boidsの位置
v::Array{Float64,2} #Boidsの速度
v1::Array{Float64,2} #rule1の出力結果
v2::Array{Float64,2} #rule2の出力結果
v3::Array{Float64,2} #rule3の出力結果
end
end
using .Boids
d=2
N=50
distThresh=10.0
ω1=0.1
ω2=0.4
ω3=1/300
maxSpeed=4.0
minSpeed=1.0
minWorld=0
maxWorld=150
worldSize=abs(maxWorld-minWorld)
param1=Boids.Param(d,N,distThresh,maxSpeed,minSpeed,maxWorld,minWorld,ω1,ω2,ω3)
p=rand(N,d).*worldSize
v=(rand(N,d).-0.5)
v1=zeros(N,d)
v2=zeros(N,d)
v3=zeros(N,d)
var1=Boids.Variables(p,v,v1,v2,v3)
#出力結果格納変数の初期化
function clear_vec(var)
var.v1.=0.0
var.v2.=0.0
var.v3.=0.0
end
#rule1 Collision avoidance
#仲間を避ける
function rule1(param,var)
for i in 1:param.N
for j in 1:param.N
if i==j;continue;end
dist=norm(var.p[j,:].-var.p[i,:])
#ある仲間jとの距離が一定の距離より短ければ
if dist < param.distThresh
var.v1[i,:].-=(var.p[j,:].-var.p[i,:])
end
end
end
end
#rule2 Velocity Matching
#群れの平均速度に合わせる
function rule2(param,var)
for i in 1:param.N
for j in 1:param.N
if i==j;continue;end
var.v2[i,:].+=var.v[j,:]
end
end
var.v2.=var.v2./(param.N-1)
var.v2.=var.v2.-var.v
end
#rule3 Flock Centering
#群れの中心に向かう
function rule3(param,var)
for i in 1:param.N
for j in 1:param.N
if i==j;continue;end
var.v3[i,:].+=var.p[j,:]
end
end
var.v3.=var.v3./(param.N-1)
var.v3.=var.v3.-var.p
end
#速度制限
function limit_vel(param,var)
for i in 1:param.N
speed=norm(var.v[i,:])
clamped=clamp(speed,param.minSpeed,param.maxSpeed)
var.v[i,:].*=(clamped/speed)
end
end
#境界判定
function check_boundary(param,var)
for i in 1:param.N
for n in 1:param.d
if ((var.p[i,n]<param.minWorld && var.v[i,n]<0) || (var.p[i,n]>param.maxWorld && var.v[i,n]>0))
var.v[i,n]*=-1.0
end
end
end
end
function update(param,var)
clear_vec(var)
rule1(param,var)
rule2(param,var)
rule3(param,var)
var.v.+=param.ω1*var.v1+param.ω2*var.v2+param.ω3*var.v3
limit_vel(param,var)
var.p.+=var.v
check_boundary(param,var)
end
const dt=1.0
@time anim = @animate for m in 0:300
t=round(m*dt,digits=2)
quiver(var1.p[:,1],var1.p[:,2],
quiver=(var1.v[:,1].*5.0,var1.v[:,2].*5.0),
xlab="x",xlims=(minWorld-10,maxWorld+10),
ylab="y",ylims=(minWorld-10,maxWorld+10),
leg=false,
title="Boids,t = $t")
plot!(var1.p[:,1],var1.p[:,2],seriestype=:scatter,markersize=2)
update(param1,var1)
end
@time gif(anim,"tmp/Boids4.gif",fps=10)
出力
9.440260 seconds (71.71 M allocations: 2.217 GiB, 6.52% gc time)
1.541061 seconds (675 allocations: 38.266 KiB)
概説に示したgif動画が出力されます。
感想
-
quiverはベクトル場のような格子点から矢印が生えているような図を描くのに使われているのをよく見ます。今回は邪道的に使って移動する矢印を描画するのに使ってます(大きさを分かりやすくするために5.0をかけています)。 - コードの分かりやすさを優先してルールごとにforループを回しています。これを一緒くたにしてやればもっと計算時間を短くできそうな気がします。
- 加速度もいれるともっとリアルになると思います。
参考文献
- [C. W. Reynolds, "Flocks, Herds, and Schools: A Distributed Behavioral Model", Computer Graphics, 21(4), 1987, pp. 25-34.]
(http://www.cs.toronto.edu/~dt/siggraph97-course/cwr87/) - "Boids Background and Update" by Craig Reynolds
- @takashi "インタラクティブプログラミング - 群れ(boid)を作る"
- Yutaka Kachi, "Boid"
- ワンダープラネットデベロッパーブログ 2015年3月13日号
- JavaScript, HTML5で『群れ』をシミュレーションするレシピ (ボイド)