目的
- Swarm Oscillatorsの数値計算
- Julia v1.0を試す
- Jupyter notebook
Swarm Oscillatorsのモデル
Swarm Oscillatorは直訳すれば「群れ動く振動子」であり、その名の通り、周辺との相互作用により集団的な挙動を見せます。Swarm oscillatorモデルは、内部自由度と空間自由度を持つ素子が相互作用する多素子系のモデルです。
素子はそれぞれ内部状態(位相)$\psi$を持ち、位置$\boldsymbol{r}$に存在するとします。
平面上に$n$個の粒子が存在するとき、それらの内部状態(位相)は$n$行ベクトル$\boldsymbol{\psi}$、位置は$n$行2列行列$\boldsymbol{r}$とおきます。このとき、$i$番目の粒子の位相は$\psi_i$、位置は$\boldsymbol{r_i}$です。$i$番目の粒子と$j$番目の粒子における位相の差を$\Psi_{ji}=\psi_j-\psi_i$、位置の差をベクトル$\boldsymbol{R_{ji}}=\boldsymbol{r_j}-\boldsymbol{r_i}$とおくと、$i$番目の素子の時間発展は
\begin{align}
\frac{d}{dt}\psi_i &= \sum_{\{j|j\neq i\}}e^{-|\boldsymbol{R_{ji}}|}\sin(\Psi_{ji}+\alpha|\boldsymbol{R_{ji}}|-c_1)\\
\frac{d}{dt}\boldsymbol{r_i}&=c_3 \sum_{\{j|j\neq i\}}\boldsymbol{\hat{R}_{ji}} e^{-|\boldsymbol{R_{ji}}|}\sin(\Psi_{ji}+\alpha|\boldsymbol{R_{ji}}|-c_2)
\end{align}
で書き表されます。ここで、$\boldsymbol{\hat{R}_{ji}}$は規格化されたものであることを示します。
イメージとしては、素子が位相$\psi$に応じてz軸方向に振動している感じです。素子自身からの距離に応じて指数減衰する正弦波の(つまり同心円状の)場があり、それが他の素子の位相や位置に影響を与えるといったような感じでしょうか。
数値計算
using LinearAlgebra
using Plots
gr(size=(340,300),titlefont=font("sans-serif",9))
const n=50 #素子数
const L=25 #系のサイズ
const c1=1.5
const c2=0.5
const c3=2.0
const α=0.5
const dt=0.05 #時間刻み
function dψ(ψ,r)
a=zeros(n)
for i=1:n
sum=0
for j=1:n
if j==i; continue;end
sum+=exp(-norm(r[j,:]-r[i,:]))*sin(ψ[j]-ψ[i]+α*norm(r[j,:]-r[i,:])-c1)
end
a[i]=sum
end
return a
end
function dr(ψ,r)
a=zeros(n,2)
for i=1:n
sum=[0,0]
for j=1:n
if j==i; continue; end
sum+=(normalize(r[j,:]-r[i,:]).*exp(-norm(r[j,:]-r[i,:]))*sin(ψ[j]-ψ[i]+α*norm(r[j,:]-r[i,:])-c2))
end
a[i,:]=sum
end
return c3*a
end
function oneStep!(ψ,r)
ψ.=mod.(ψ+dψ(ψ,r)*dt,2π)
r.=mod.(r+dr(ψ,r)*dt,L)
end
function draw(gen,ψ,r)
t=round(gen*dt;digits=2)
scatter(r[:,1],r[:,2],
xlab="x",xlims=(0,L),
ylab="y",ylims=(0,L),
zcolor=ψ,
leg=false,
cbar=true,
cbarlims=(0,2π),
title="t = $t, (gen = $gen),\n c=[$c1,$c2,$c3],alpha=$α")
end
psi=rand(0:0.01:2π, n)
pos=rand(0:0.01:L,n,2)
@time anim = @animate for m in 0:5000
oneStep!(psi,pos)
draw(m,psi,pos)
end every 100
@time gif(anim,"tmp/swarm_osillators.gif",fps=4)
26.595608 seconds (263.93 M allocations: 22.255 GiB, 11.16% gc time)
0.633165 seconds (701 allocations: 39.125 KiB)
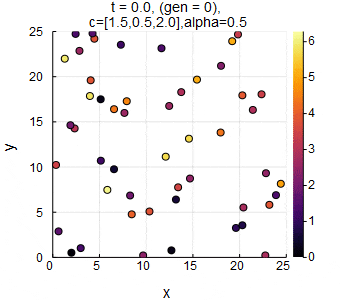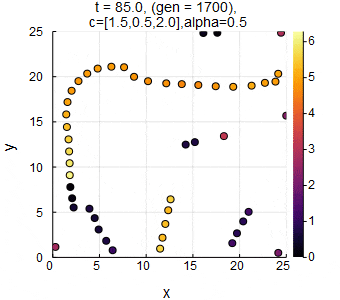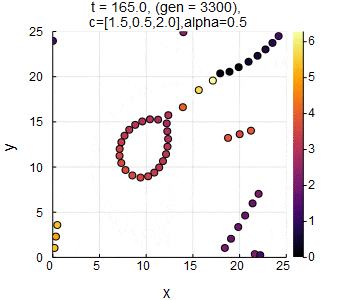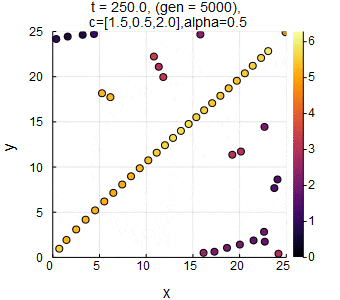
$n=50,L=25,c_1=1.5,c_2=0.5,c_3=2.0,\alpha=0.5,dt=0.05$のときのSwarm Oscillators(動的曲線相).
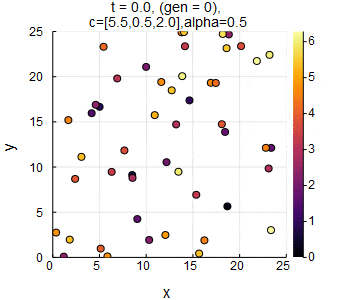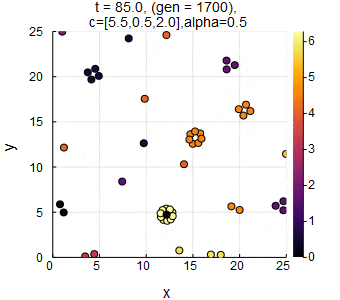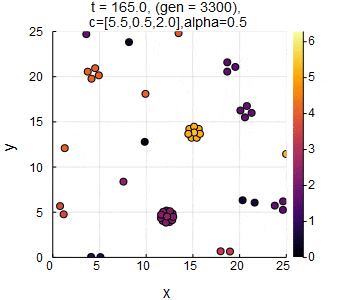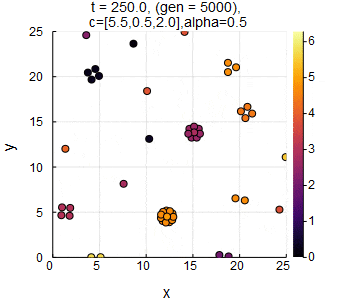
$n=50,L=25,c_1=5.5,c_2=0.5,c_3=2.0,\alpha=0.5,dt=0.05$のときのSwarm Oscillators(凝集相).
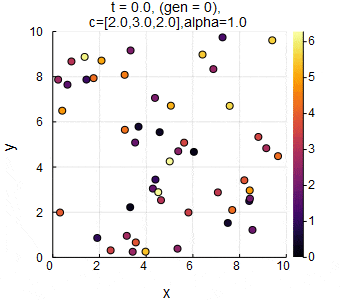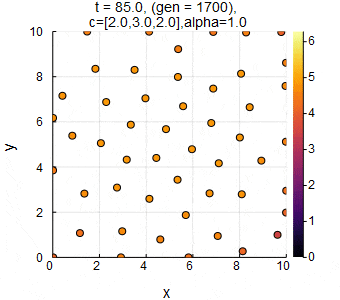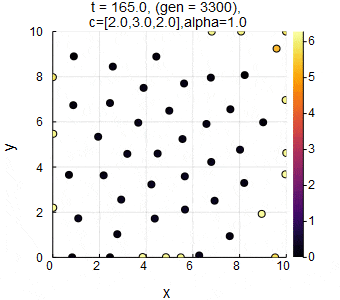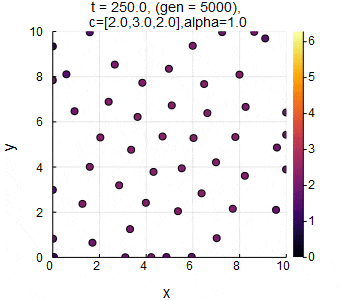
$n=50,L=10,c_1=2.0,c_2=3.0,c_3=2.0,\alpha=1.0,dt=0.05$のときのSwarm Oscillators(格子相).
6つのパラメータ$n,L,c_1,c_2,c_3,\alpha$を調節することで様々な集団的挙動を示します。
つまづいたところ
標準ライブラリの読み込み
Julia v1.0から標準ライブラリがBase.以下ではなくなったため、使うときは明示的にusingする必要があります。今回の場合、normalizeを使うためにusing LinearAlgebraと書かなければいけません。
constの威力
グローバル変数にconstをつけるとだいぶ早くなる(~100sec -> ~25sec)
round
以前は
round(m*dt,3)
で3桁表示ができた。現在は
round(m*dt;digits=2)
で小数第2位まで表示指定するようになっている。コンマではなくセミコロンであることに注意。(20180918追記)セミコロンでなくコンマでもOKです。
round(m*dt,digits=2)
NEORTにも投稿しました
WebGL+領域分割