複数の特徴量で学習するときの注意について自分なりにまとめてみました。
※当初「次元の呪いとは何なのか」というタイトルにしていました不正確だという指摘を複数受けタイトル名を変えました申し訳ないです。時間が取れれば勉強し直して記事を書き直したいと思います。
多数の特徴量で学習するときの問題点
機械学習を勉強し始めた人であれば、特徴量が多いとうまく学習できない、いわゆる次元の呪い(The curse of dimensionality)という言葉は聞いたことがあると思います。
例えば問題の1つとして、説明変数を増やしすぎると過学習しやすくなるという問題があります。
最初に結論
次元の呪いとは高次元データが、実態としてはもっと低次元だったから起こる問題です。
よくある説明
次元の呪いの説明としてよくあるの説明が多次元の球の体積を使った説明です。高次元の球では、ほとんどの部分が球の表面付近に分布する、という説明です。
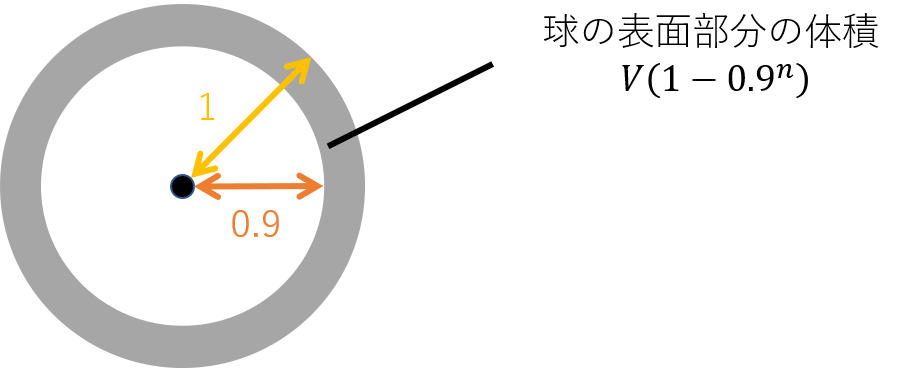
上のように半径1の球と、その中に半径0.9の部分球があったとします。球全体の体積を$V$とすると、球の表面部分の体積は$V(1-0.9^n)$と表せます。これは例えば$n=20$の20次元では実に球の体積の88%を占めることになります。
つまり、データが高次元だと、ほとんどのデータが空間の外側に分布してしまうことになります。
で、何が問題なのか？
この説明を聞いて、「なるほど！だから説明変数を増やしすぎるのは良くないんだ！」と素直に納得する人はどれくらいいるのでしょうか？少なくとも私はそうではありませんでした。
しかもこの説明は不十分な面もあり、たとえデータが低次元でも問題は起こりえます。また例えば正規分布のように、データが中心に偏っていて、球の外側に分布していなくてもデータの分布によっては問題が起こりえます。
最初の結論でも述べましたが、問題は次元が下がることです。
線形回帰で考えてみる
単純な線形回帰を考えてみましょう。説明変数$x$、目的変数$y$の組から、$y=ax+b$と直線の式で回帰できます。
これが説明変数が1次元の場合です。
説明変数が2次元の場合、$y$は2つの説明変数$x_1,x_2$から$y=ax_1+bx_2+c$と平面の式で回帰できます。
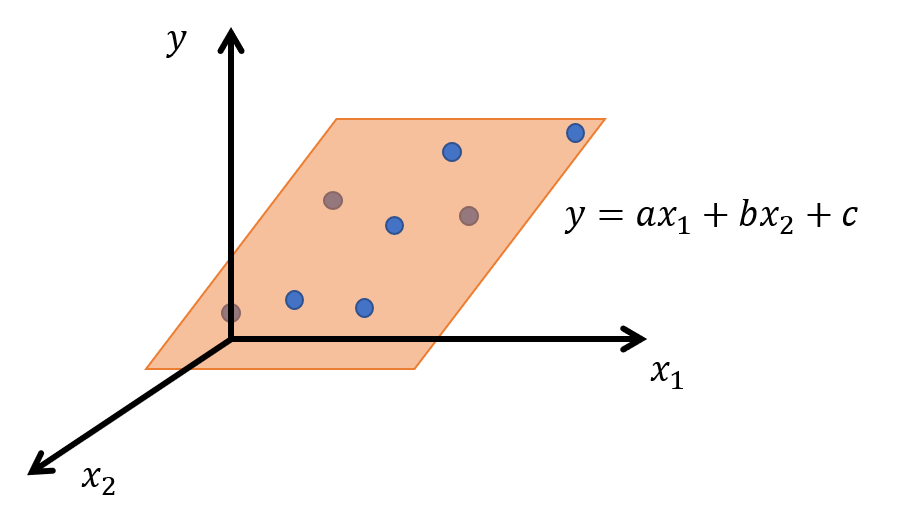
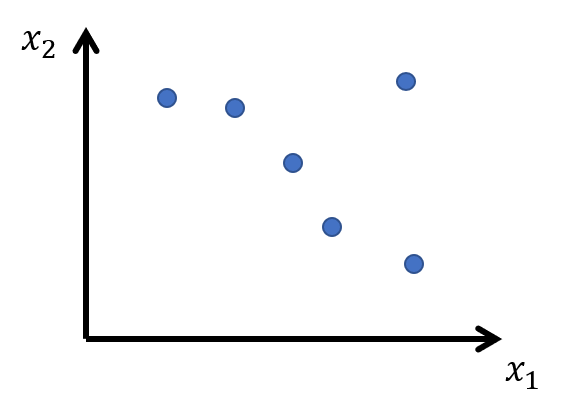
もしここでもし、ここで下のように$x_1$と$x_2$のデータの間に高い相関があり、$x_1,x_2$平面上でほぼ直線状に分布していたらどうなるでしょう？
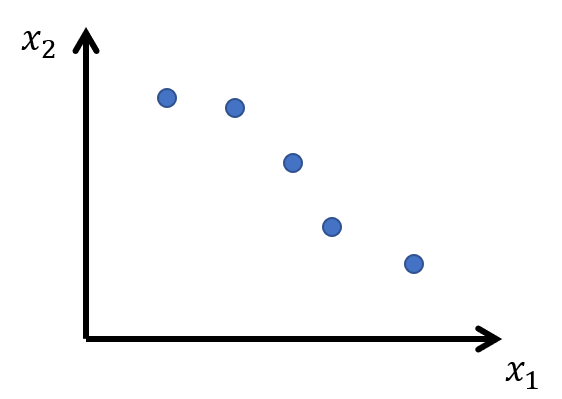
その場合下のように考えられうる回帰の平面が多くなって一意に決められなくなってしまいます。
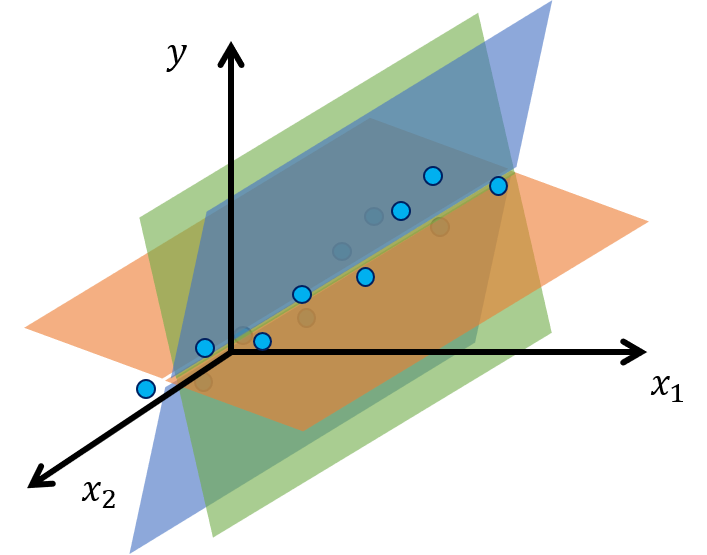
このような状態で、無理やり最小二乗法で計算すれば、回帰式を計算できますが、そのような回帰式は$x_1,x_2$の相関の直線から少しでも外れた値を正しく回帰できる保証はありません。
また下のように相関から外れたデータ1つあったとすると、
全体の回帰平面はその一つの外れ値のデータに引っ張られてします。
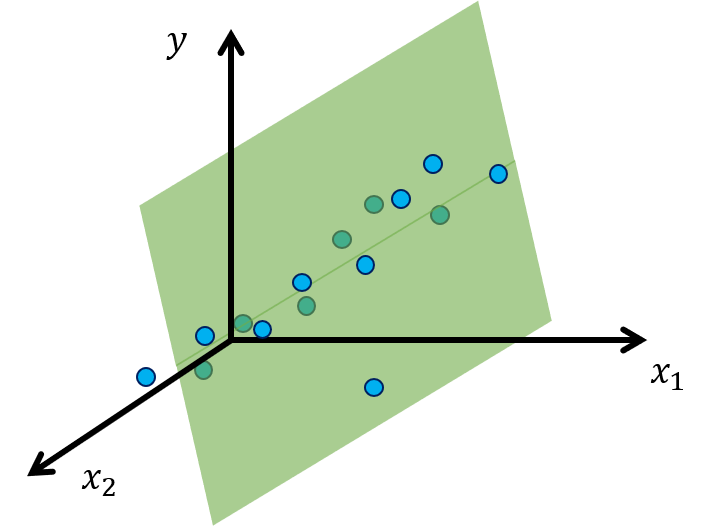
これは過学習の状態で、少数のデータによって回帰式が大きく変わってしまうため、別のデータに対してはうまく回帰できない、ということになりえます。
このように説明変数同士の相関が高すぎて正しく回帰できないことを、(次元の呪いの話とは別に)線形回帰における多重共線性と言うらしいです。
##なら相関が0ならいいのか？
では説明変数同士の相関が0であれば常に正しく回帰できるのでしょうか？例えば下図のように円周状にデータが分布している場合、常にうまく回帰できるのでしょうか？
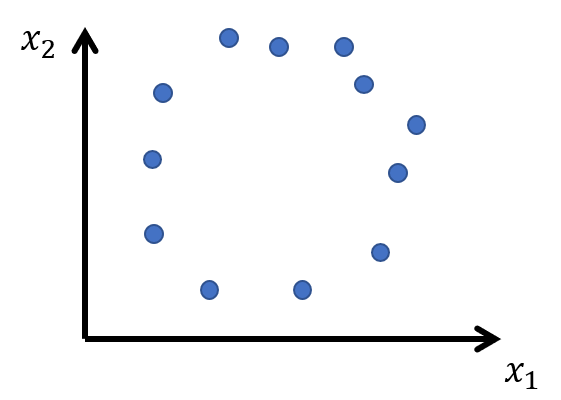
1次関数の線形回帰なら円周上に分布しているデータに対し、描ける平面は一意に決まりそうなので、正しく回帰できそうです。
しかし、他の手法ならどうでしょう？例えば$y=a_1x_1^2+a_2x_2x_1+a_3x_2^2+a_4x_1+a_5x_2+a_6$のような2次関数で回帰しようとしたとします。2変数の2次関数は放物面です。そして円周上に分布したデータに当てはまる放物面はいくつも描けそうです。
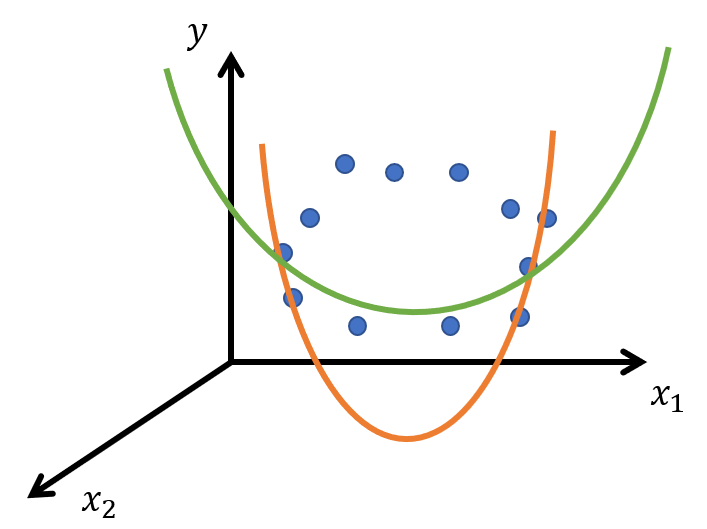
##実際より次元が低いと問題が起きる
このように、説明変数を2次元で用意したつもりでも、実際は直線や円周といった1次元のデータだった場合、正しく学習できないのです。
そして用いる学習手法や、過学習のしにくさによってそのデータをそのままの次元で扱えるかは変わってくるようです。先程の例で言えば、円周状に分布したデータは、直線の線形回帰を使えば二次元のデータとして扱えても、二次関数の回帰では1次元のデータです。
もっと複雑な決定木やディープラーニングを使った場合は、$x_1,x_2$平面上でグネグネ分布したデータであっても、1次元のデータとして扱ってしまうことが考えられます。
(また、円周が1次元なのではなく、2次関数による線形回帰では空間をより高次元空間に射影し、そこでは円周は低次元に分布しているから、という解釈もできそうです。)
つまり用意したデータがいくら高次元であろうと、実態として低次元だと、間違った学習をしてしまうのです。そしてそのデータが何次元かは用いる学習手法によって変わってくるということです。
##じゃあ球の体積の説明とはなんだったのか？
高次元だと球の体積の大部分が表面に分布するなら、球が球面になってしまいます。つまりデータの次元が一つ次元が下がってしまうことになってしまいます。
しかしこれはデータが一様分布していた場合で、独立に正規分布していた場合、20次元でも下のようにある程度空間に一様に広がっていることがわかります。
このように球の体積の例え話はいつも成り立つわけではないのです。
(※更に高次元だと、正規分布であっても球面に集中してしまうらしいですが。)
また、球の体積の話では半径にしか注目していません。
確かに半径方向に広がっているかどうかも重要ですが、半径という次元以外にもデータがまんべんなく広がっているかどうかも重要です。例えば説明変数同士に高い線形な相関があれば、半径方向にまんべんなく分布していたとしても、明らかに次元が一つ下がっています。データがまんべんなく広がっていないことになります。
##じゃあ結局次元の呪いって何よ
今まで見てきたように、次元の呪いとは、単に特徴量を増やしてはいけないという話ではなさそうです。
ここで現実の問題に立ち返ってみると、現実の問題で、独立に正規分布している特徴量がたくさんあるということは少ない思います。2つの特徴量が実際は別の原因によって発生する結果であったりして、無関係な特徴量は数個しかない、という状況もあると思います。また特徴量が正規分布していない場合もあるでしょう。カテゴリを表すデータや離散的なデータはまんべんなく分布したとしても一様分布となってしまいます。
次元の呪いとは、求めたい目的変数に関連ある特徴量のうち、それぞれ独立な特徴量を見つけてくるのが現実的に難しい、という問題な気がします。
じゃあどうすればいいの？
どうすればいいかについては私はまだまだ勉強不足ですが、いくつか言えそうなことはありそうです。
まず説明変数同士の相関が高いのは避けたいです。そしてできるなら正規分布している連続値のデータがいいでしょう。そしてより複雑な手法を用いるなら、線形の相関だけではなく、非線形の相関も確認する必要があります。
説明変数同士の相関を下げるにはどうすればいいか。まずはデータの数を増やすことが理想でしょう。上の図で述べた相関から外れた値がある、というのはいわばモデルにとっては後出しじゃんけんみたいなものです。このデータセットについて合うモデルを作れと言われたのに、後からテストデータにそのデータセットから外れたデータがあれば、モデルが合わないのは当たり前です。データをため、外れ値がたくさん貯まり、外れ値でなくなるまでデータの数を増やすべきです。
それかその外れ値については除去し、諦めるかです。
データが増やせない場合、まず高い相関がある特徴量同士は、重要そうなものを残し、他は削除します。例えばより目的変数と相関が高いほうを残すなどです。(特徴選択)
また2つ以上の特徴量から別の特徴量を作る、ということも考えられます。(特徴作成)
[](##ここまで来て勘違い
とここまで書いてよくよく調べてみたら、次元の呪いというのは高次元空間のデータ同士の距離の分散が小さくなるために、分類が難しくなるという意味で使われているのが本来の使い方らしいです。もしかしたら単に特徴量が多すぎるという問題の中で、次元の呪いの話と、ここで書いた特徴量同士の相関が高すぎる話とは、全く別の話なのかもしれないです。。。
)
##最後に
次元の呪いについて自分なりの解釈をまとめてみました。まだまだ勉強中なので間違い等多々あると思いますが、参考になれば幸いです。