今回も前回に引き続きRによる統計的学習をまとめて行こうと思う。
この記事で使用するグラフ、表は全て本書の公式サイトから引用させてもらった。
Some of the figures in this article are taken from "An Introduction to Statistical Learning, with applications in R" (Springer, 2013) with permission from the authors: G. James, D. Witten, T. Hastie and R. Tibshirani.
なおこの記事では具体例などはすっ飛ばしていきなり一般化させて頂く。
2 統計的学習
2.1 統計的学習とは
$p$個の異なる予測変数 $X_1,....,X_p$から量的な応答変数$Y$を得たとする。$X$と$Y$の間に何らかの関係があるとすると次のように書ける。
$$Y=f(X)+\epsilon$$
ここで$f$は$X$についての未知の関数であり、$\epsilon$は$X$とは無関係で平均が$0$であるランダム誤差項である。
統計的学習はこの$f$を求めるために使われる色々な手法のことである。
2.1.1 なぜfを推定するのか
$f$を推定する理由は予測と推論の2つある。
予測
多くの場合、入力変数Xは簡単に観測できるが出力変数$Y$は簡単に観測できない。そこで$Y$を予測するには以下の式を用いる。
$$\hat{Y}=\hat{f}(X)$$
$\hat{f}$は$f$を推定したもので$\hat{Y}$は$\hat{f}$によって推測されたものである。つまり$f$を推定する理由は$Y$を推定するためである。
$\hat{Y}$を推測するために削減可能誤差と削減不可能誤差の二種類の誤差がある。
削減可能誤差は$\hat{f}$は$f$の推定を完璧にできないことによる誤差である。これはベストマッチな手法を使うことで$f$を推定することでより完璧なものに近づくことから削除可能と呼ばれる。
削減不可能誤差は2.1でも述べた、$X$と$Y$の関係の第二項$\epsilon$によって生まれる。この $\epsilon$は入力変数$X$以外に$Y$に影響を与えたものから発生するものである。これは測定してないからわからないし誤差を埋めようがない。(埋めたら過学習になるしね。)
推論
先ほどまでは$Y$の値を知りたいということだったが、我々は必ずしも$Y$の値を知りたいなんてことはなく、$X$が変わると$Y$がどう変化したいのかを知りたいこともある。つまり$\hat{f}$がどのような関数なのかを知る必要がある。この場合これらの答えを知る必要がある。
・たくさんの入力変数のうち出力変数に影響を与えているのがごく少数だったりするので、入力変数を絞ったりするのは非常に役に立つことである。
・入力変数と出力変数の関係(たとえば正の相関だったり。。。)を知ることも有効である。
・入力変数と出力変数の関係は線形か非線形なのかなどを知ることでその関係を正確に表すことができる。
予測をしたいのか推論をしたいのかそれまた両方したいのかによって$\hat{f}$を推定する上で異なった方法を行う。例えば線形モデルを使えば目に見えて関係がわかることが多いので推論をしやすいが予測するには誤差がありすぎる。逆にほぼ完璧に非線形の関係などを予測できたとしても、その関係が目に見えてわかりやすいとは限らない。
2.1.2 どのようにfを測定するか
$f$を推定するにはパラメトリック法とノンパラメトリック法のに種類がある。これは言葉通りでパラメトリック法は$f$の形を最初から決めて推測するので、パラメーターを推定するだけである。これに対してノンパラメトリック法は$f$の形を推定せずに行うものである。
それぞれもちろん長所短所がある。パラメトリック法は簡単に$f$を推定できるが$f$の形の推定が間違っていたら本来の$f$と全然違うものとなる。ノンパラメトリック法は多くの種類の$f$に対して正確に$f$の当てはめができるが、観測値が大量に必要だったり、過学習になることも多い。
2.1.3 予測精度とモデルの解釈のしやすさのトレードオフ
色々な手法による解釈のしやすさ(Interpretability)と柔軟さ(Flexibility)を以下の図に示した。(和訳すると上から、部分集合選択Lasso、最小二乗、一般化加法モデル、木、バギング、ブースティング、サポートべクターマシン、Lassoが日本語じゃないというのはやめてください。)
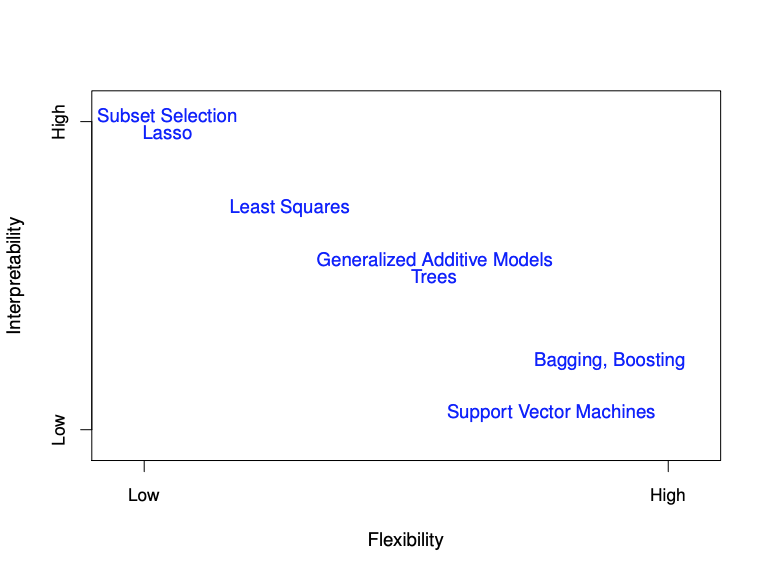
ちなみにトレードオフはどちらか一方を立てるともう一方が沈むみたいな意味。
2.1.4 教師あり学習と教師なし学習
ほとんどの統計的学習は教師あり学習と教師なし学習に分けられる。
教師あり学習は、応答変数$Y$があるものである。それに対して教師なし学習は応答変数がない。
教師あり学習は容易に想像できるしありふれているので説明はしない(今まで扱ったもの全て教師あり)が、なしの場合のみ念の為詳しく説明しておく。教師なし学習は変数の関係や観測データ同士の関係を調べることなどがある。以下の図を見てもらえばわかると思う。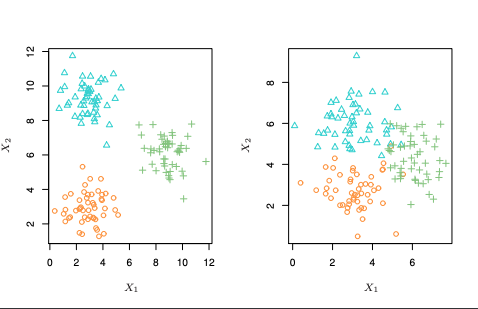
教師あり学習と教師なし学習に明確に分けれないものも存在する。
2.1.5 回帰問題と分類問題
また出力変数のカテゴリーとして回帰問題と分類問題というものがある。量的変数であれば回帰問題だし、質的変数であれば分類問題である。量的というのは身長などの数値を取る。質的は性別など数値で表せないものなどがある。この場合男を1として女を0とする事がある。(男が1じゃなくてもいい。女が1でももちろん結果は変わらない。)
2.2 モデルの制度の評価
2.2.1 当てはめの質を測定する
fを推定した結果、真のfにどれだけ近いかを測定することは極めて重要である。今回帰モデルで最も広く使われているものを紹介する。
平均二乗誤差(MSE:Mean Squared Error)
$$MSE = \frac{1}{N}\Sigma^n_{i=1}(y_i-\hat{f}(x_i))^2$$
である。これは入力$x_i$に対する真のyと推定したyの差の二乗の平均を取ったものである。ある観測値のyと推定したyが大きく異なればこの値が大きくなる(二乗しているのはもちろん入力$x_i$に対する真のyと推定したyの差が正になったり負になったりするので、+とーでこの差を是正させないため)。
MSEを訓練データのみで計算したものを訓練MSE、テストデータのみで計算したものをテストMSEという。訓練MSEが小さくなることももちろん大事だが、我々が知りたいのは未知の入力に対してどれくらいの精度で推定できるかなのでテストMSEが小さいものが大事になってくる。訓練MSEを小さくすればテストMSEも小さくなると何も考えないと思ってしまうが訓練MSEを小さくすることだけ考えると過学習を起こしてテストMSEが大きくなる可能性が高い。
こういうことを聞くとテストデータがないときどうすればいいんだと思うが、後々紹介する交差検証やブーストトラップを学ぶことでわかる。
### 2.2.2 バイアスと分散のトレードオフ
分散とバイアスという言葉についてまず説明する。
分散とは異なる訓練データを使ったときにどの程度$\hat{f}$が変化したか表す量である。
バイアスとは極めて複雑な現象を近似した為に生じる誤差のことである。
もしバイアスを抑える為にfの推測する柔軟さをあげると、分散の値が大きくなる。逆もまた然り。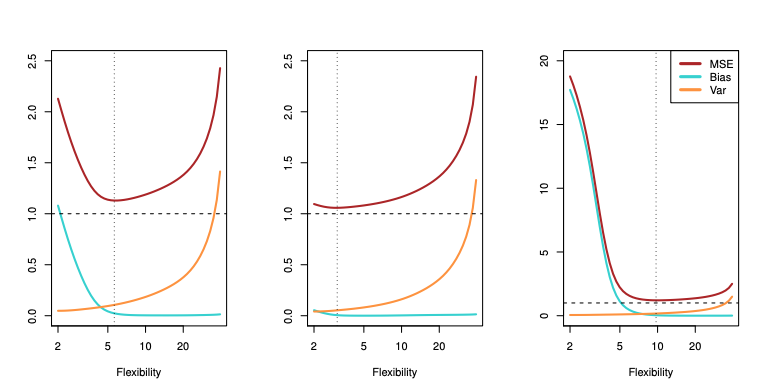
上図の通り、バイアスを抑える為に柔軟さをあげると分散が大きくなる。(点線は削減不可能誤差)3つの図それぞれ真の柔軟さが異なる為違った曲線を描く。真の曲線は左から
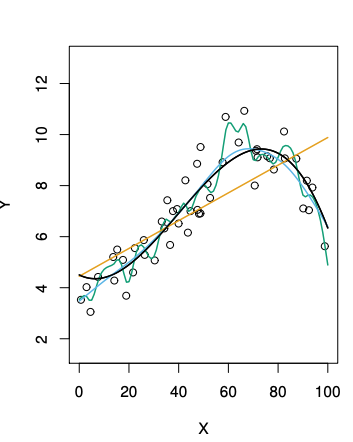
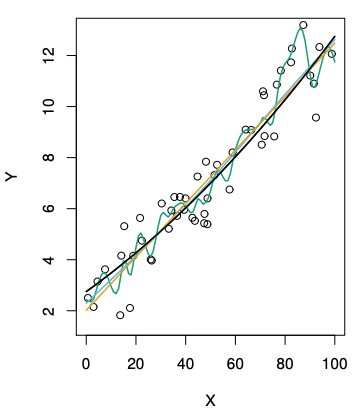
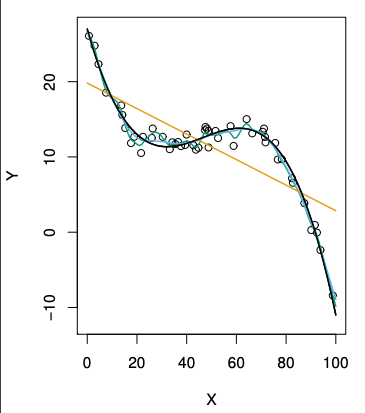
となっている(黒線)。これを見比べるとなぜ最初の図が異なった曲線を描くのかわかる。
2.3.3 分類における制度の評価
これまで回帰について議論してきた。次に分類ついて議論する。$\hat{f}$の推定の精度測るのに最もよく使われるのは推定値$\hat{f}$を訓練データに使った時の誤分類になる割合であり、訓練誤分類率と呼ばれる。
$$\frac{1}{n}\Sigma^n_{i=1}I(y_i\neq\hat{y_i})$$
$I$は$y_i\neq\hat{y_i}$の時に1を返し$y_i=\hat{y_i}$の時0を返す指示関数である。もちろんこれもテストデータをこれに代入したテスト誤分類率の方がより興味の対象となる。
ベイズ分類機
ある予測変数が与えられた上で最もらしいクラスに分類するというとても単純な分類機が、テスト誤分類率を最小化することができる。つまり予測変数ベクトル$x_0$のテストデータを
$$Pr(Y = j | X = x_0)$$
が最大になるようなクラスに分類するのである。このとても単縦な分類機をベイズ分類機という。ベイズ分類機は$Pr(Y = 1 | X = x_0) > 0.5$の時クラス1、そうでなければクラス2に属すると予測する。一般にベイズ誤分類率は
$$1 - E({max}_j Pr(Y=j|X))$$
である。
k最近傍法
K最近傍法とはある整数$K$とテストデータ$x_0$が与えられ訓練データのうち$x_0$に最も近いK個のデータを探し、これを要素とする集合 $N_0$とし、
$$Pr(Y = j | X = x_0) = \frac{1}{K}\Sigma_{i\in N_0}I(y_i = j)$$
を求め、ベイズの法則を使い、テストデータ $x_0$を最も確率の高いクラスに分類するものである。