はじめに
botterの皆さん、メリークリスマス!スナフキンです。
今年も残り1週間となりました。今年1年を振り返ると、ぼくは仕事、不動産、釣り!という感じの2022年を過ごしまして、今年は意識的にあまり真面目にbotに取り組む時間を取らず、昔作ったbotをメンテしながら細々と運用するという感じでした。
しかしながら、釣りでは昔から親交のある老害古参botterであるらっちょさん(https://twitter.com/rc_uni0907)や、DEX沼にハマって人間をやめてしまったDEXデュエリストことRosさん(https://twitter.com/Ros_1224)、コワーキングスペースオーナーのJunさん(https://twitter.com/Freeza_BtcBot)と交友を深めるなど、みなさんのおかげで楽しい1年を過ごせました。
さて、そんな感じで今年は半分botを引退してしまっていたようなぼくなのですが、Twitterで何か書くと宣言してしまった手前、題材を考えなければまずい、困ったなーと首をくねくねさせていたところです。
苦渋の末に捻り出した題材として、古参botterらしく、新規で入ってきた方に向けて昔話をうざったく仮想通貨bot業界の歴史を語りつつ、どういったスキルセット、素養がある方がbotに向いていて、反対にどういった方は、#botは儲からないからやめた方がいいのかを考える記事としたいと思います。
参考(botはやめた方がいいと口々につぶやくbotterたち):https://twitter.com/hashtag/botは儲からないからやめた方がいい?src=hashtag_click
こうして眺めてみると、皆さんポジショントーク的に、競合を増やしたくないためにbotはやめたほうがいいと言っているところが少なからずあるとは思いますし、ぼく自身もそう思っていた時期もあります。
しかしながら、bot開発から少し距離を置いてそれ以外の色々な経済活動をやってみた今改めて思うところとして、やはり自分自身のスキルセット・素養を冷静に客観的に見た上で取り組む対象を選ぶことの重要さを実感しており、ポジトークとしての意味だけではない、この言葉の真の意味を皆さんにお伝えする必要があるのではないかと思い、この度筆を執らせていただきました。
去年のアドベントカレンダーに続いてのポエム記事になりますが、お付き合いのほどよろしくお願いします。
仮想通貨取引bot開発に必要なスキルセットとbot界隈の歴史
bot開発に必要なスキルセット
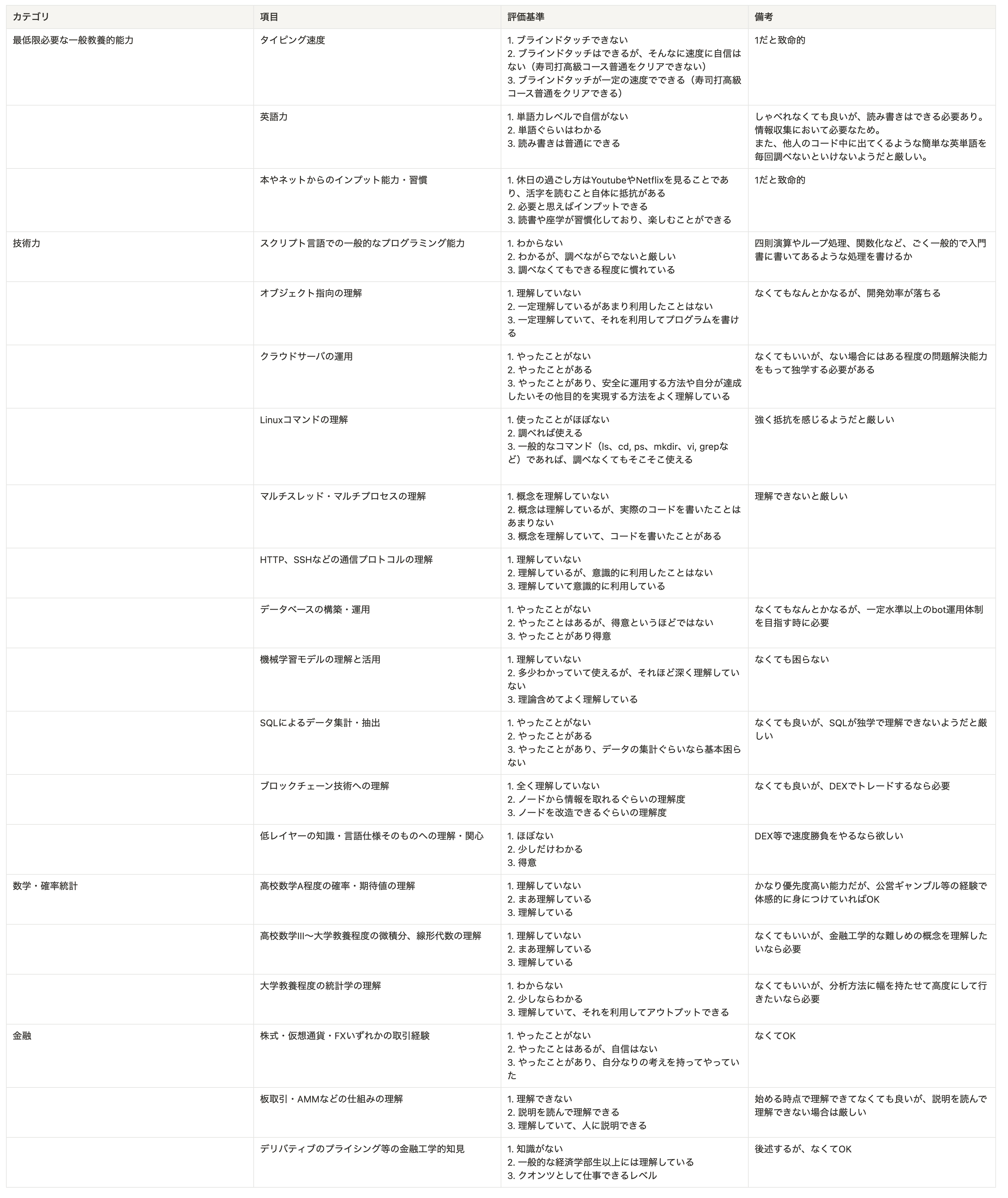
bot開発に必要なスキルセットと言っても様々ではありますが、QASHさんの上記ツイートは非常に的を射ていると考えており、これをさらに分解すると、概ね以下の表のような感じになると考えています。(文字小さくてすみません)
体感として、全ての項目の平均値が1.8以上ぐらいであれば、bot開発を始めて1年以内に勝てるようになる可能性が10〜20%ぐらいある気がします。ちなみに、1-3の3段階で評価基準を書いていますが、当然これ以上の水準もあると思います。
表に記載したスキルセットのうち、どの項目の重要度が高いかというのも、業界の流行によって変わってきました。
仮想通貨botの歴史
ぼくが参入した2017年秋のちょっと手前ぐらいから業界の歴史を振り返ると、次の表のような推移だったと記憶しています。歴史の概観とともに、当時の様子が分かるような記録や当時名を馳せていた方を掲載して行きます。
- 2016年〜2017年前半
- ヨーロピアンさんや田中さんのような先駆者が人知れずbotトレードを行う
- 2017年後半〜2018年末
- 国内CEX最盛期。バブル崩壊後のボラティリティが大きい相場で、競合が少ないため非常に稼ぎやすい環境だった
- 当時はbitFlyerFXの損益グラフがTwitterを埋め尽くしていた。AKAGAMIさんのイナゴbotやドテン君がbotトレードを世に知らしめる
- 2019年〜2020年前半
- 国内CEXの出来高がバブル崩壊後小さくなっていき、botterたちの元気がなくなる。この時期は裁量トレーダーのサロンや、botを販売する動きが増える。
- 2020年後半〜2021年前半
- DeFiサマーと言われるようなDeFiの流行とともに、UniswapなどのDEXを主戦場とするbotterが目立ち始める
- 2021年後半〜2022年前半
- DEX botterという言葉が一般的になり、人間をやめなければ勝てない程度にDEXの競争が激しくなる
歴史の推移と必要とされるスキルセットの変遷
上記のような歴史の変化とともに、botterに必要とされるスキルセットの重要度も変化していきました。
分かりやすい対比として、CEX・DEXという軸で必要とされるスキルセットの違いを考えると、次のような違いがあると思っています。なお、あくまでも典型的なパターンを考えており、これに当てはまらないものもたくさんあると思いますがご容赦ください。
- CEX
- 有効な投資指標(特徴量)の探索、特徴量を利用した予測モデルの構築など、比較的金融・数学・ギャンブル理論的な素養が求められる
- 技術力については、データを蓄積、集計・分析・可視化するための環境構築や、注文執行を効率的に行うためのマルチスレッド・マルチプロセスの理解、bot運用環境であるクラウドサーバの構築力や、速度的優位性を得るためのリージョン選定など、比較的表層的な最低限の知識・経験でOK
- 技術的な参入障壁が比較的低いため、それ以外の能力での競争は激しくなりがち
- DEX
- いち早く新興チェーンの裁定機会に気づき、その裁定機会を拾いにいけるだけの技術的なキャッチアップ能力が求められる
- CEXでの取引で必要とされる知識・経験に加え、より低レイヤーの知識経験やブロックチェーン技術の理解が求められる
- 技術的な参入障壁が比較的高いため、競合の数は少なくなりがち(競争が激しくないということではないですが。)
ざっくり言うとこの1-2年の潮流としては、DEXの流行によって盛り上がっている市場への技術的参入障壁が上がり、技術的なレベルが低い筆者のような老害botterがついていけなくなってしまったという流れだと思います。
筆者としては、この冬の機会に技術力を底上げし、次の仮想通貨バブルで技術力で引けを取らないようにしていきたいと考えています。
なお、よく聞かれることなのですが、どちらの分野においても、難し目の金融工学的な知見はあまり必要ないと考えています。
というのも、暗号資産のアビトラやそれに類する取引というのは、例えるなら自動販売機の下に落ちているお金をひたすらに拾い続ける行為のようなものであり、金融工学的知見というのは、世の中の自販機の特徴を色々と抽象化して行った時に、どのような特徴を持っている自販機の下に、どのような確率でお金が落ちているかを一般論として語る理論に近いと考えているためです。
もちろん、その知見はどこから探し始めるかを考える、つまり仮説を立てる段階で有効ではあるものの、結局のところ、生の自販機の下をたくさん見てお金を探しにいくことや、ライバルの自販機金拾い人に対して如何に速く拾う技術をつけるかということの方が重要度が高いのです。
結局一番重要な能力は自身の相対的優位性を把握する能力
さて、色々な能力について記載してきましたが、個人的には最も重要な能力は、自身の相対的優位性を把握する能力、すなわちメタ認知力だと考えています。
その競争環境の中で勝者になれるかというのは、上述したような各種の能力が絶対的に高い低いということではなく、その競争環境の参加者の中で自分が優位に立てるかによって変わります。
よって、自分自身は各種能力値について、市場参加者全員と比較してどれぐらいの位置にいるのか、どれぐらいの位置以上にいられれば勝者になれるのかということを把握することこそができ、その上で自分に優位性があるならば、上の表に書いたような能力の絶対値については、その瞬間に勝つことに対しては全く関係ないと言っても過言ではありません。
(もちろん、その勝利を長く継続するためには、能力の絶対値を上げ続け、新規に能力値が高い人が入ってきても勝ち続けられるように準備しておく必要があります)
さて、ここで上述した相対的優位性の重要さをより直感的に理解するために、ちょっとしたシミュレーションをしてみようと思います。
シミュレーションの設定
シミュレーションは以下の設定で思考実験を行います。
- 市場参加者の能力と市場マッチ度、優位性
- それぞれ異なる優位性を持つ市場参加者が1,000人いるとします。これらのうち、i番目の参加者を$U_i$と呼びます
- 市場参加者が持つ能力は、a, b, c…, jの10個の項目からなり、それぞれの能力のその市場へのマッチ度合いA, B, C, …, Jという概念があるとします
- 市場参加者の持つ優位性$S$とは、市場参加者の持つ能力とマッチ度合いをそれぞれ掛け合わせて、全ての積を足したもの、つまり$S = aA + bB + ...... + jJ$$aA + bB + ...... + jJ$として、1つの数値で表されるものとします
- なお、a〜j, A〜Jは、多種多様な能力からなる1人の能力を1つの量として表現する方法を具体的に説明するために置いているだけで、シミュレーション上は特に使いません
- $U_i$の優位性は、$S_i$と表されるものとします
- $S_i$は平均1, 標準偏差0.3の正規分布に従うものとします
- つまり、ここでは参加者のうち約70%の人が、せいぜい30%程度の能力差、参加者のうち99%の人としても能力差2倍以内の範囲に収まり、市場参加者間の能力差がわずかであるケースを想定しています
- 富の初期値
- 市場参加者は全員、初期値として10,000の富を所有しているとします
- 取引による富の移動
- 市場参加者から2人をランダムに選び、この市場参加者2人(j, k)は「取引」を行います
-
取引は、定額(100)または所有している富に対する定率(1%)を使って行います
- まずは定額パターンでシミュレーションします
- ランダムに選んだ2人の市場参加者の優位性を$S_j, S_k$とします
- 取引に勝った方は、2人が取引に利用した富を全てもらえることとします
- 取引に勝利する確率は、j, kそれぞれ${S_j}/(S_j + S_k), S_k/(S_j + S_k)$ であるとします
- 市場参加者の退場
- 市場参加者の富が2,000未満となった場合、市場参加者は市場への参加をやめ、これを退場と呼ぶこととします
上記設定を次のように実装します。
import numpy as np
import random
import matplotlib.pyplot as plt
import copy
# 市場参加者を設計します
class User:
def __init__(self, superiority):
self.n_trades = 0
self.capital = 10000
self.capital_history = []
self.update_capital()
self.superiority = superiority
def bet_capital(self, bet):
if bet > 1:
self.capital = self.capital - bet
elif 1 >= bet >= 0:
bet = self.capital * bet
self.capital = self.capital - bet
self.n_trades += 1
return bet
def update_capital(self):
self.capital_history.append(self.capital)
def calculate_record(self):
# 取引ごとの損益の計算
self.pl_history = np.diff(self.capital_history)
# 1000取引の勝率を時系列の移動平均で計算。勝ち:1, 負け:0で符号化
self.win_lose = list(map(lambda x: 1 if x>0 else 0, self.pl_history))
self.win_rate_mvavg = np.convolve(self.win_lose, np.ones(1000), mode="valid") / 1000
# 1000取引の損益の移動平均を計算
self.pl_mvavg = np.convolve(self.pl_history, np.ones(1000), mode="valid") / 1000
# 市場参加者の数は1000人
n_users = 1000
# 優位性順に並び替えて初期化
users = [User(s) for s in sorted([np.random.normal(1, 0.3) for i in range(n_users)], reverse=True)]
# 取引を実行する
def trade(users):
u1, u2 = random.sample(users, 2)
u1_bet = u1.bet_capital(100)
u2_bet = u2.bet_capital(100)
p1 = u1.superiority / (u1.superiority + u2.superiority)
p2 = u2.superiority / (u1.superiority + u2.superiority)
winner = np.random.choice([u1, u2], p=[p1, p2])
winner.capital += u1_bet + u2_bet
u1.update_capital()
u2.update_capital()
return u1, u2
# シミュレーション
def simulate(n_trades, users):
bankrupts = []
for i in range(n_trades):
u1, u2 = trade(users)
# 退場処理
if u1.capital < 2000:
bankrupts.append(u1)
users.remove(u1)
if u2.capital < 2000:
bankrupts.append(u2)
users.remove(u2)
return users, bankrupts
# 市場参加者の優位性の分布を可視化
bins = plt.hist([u.superiority for u in users], bins=20)
plt.title("Superiority histgram")
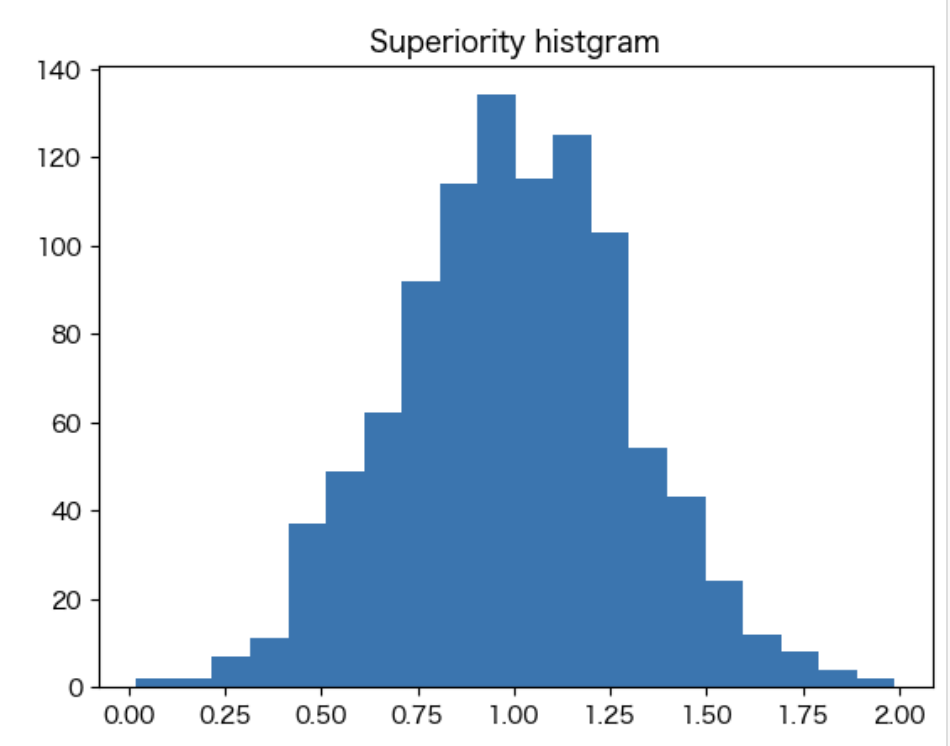
↑優位性の分布は高々上下100%であり、市場参加者同士の能力差は小さいという仮定を置いています
取引回数と観測対象
市場全体での合計取引回数を300,000回、1,000,000回、3,000,000回、と変化させたとき、次のデータがどう変化するかを観測し、その観測をもとに、市場参加者の相対的優位性が重要であることを示します。
- 市場参加者の富の分布
- 市場参加者の優位性と富の散布図
- 市場参加者のうち、優位性が上位30番目(全市場参加者を母集団としたとき上位0.3%)の市場参加者(=対象者と呼びます)の富の時系列推移
- 対象者の勝率・損益の1000取引移動平均の時系列推移
シミュレーション結果と解釈
定額で賭ける場合
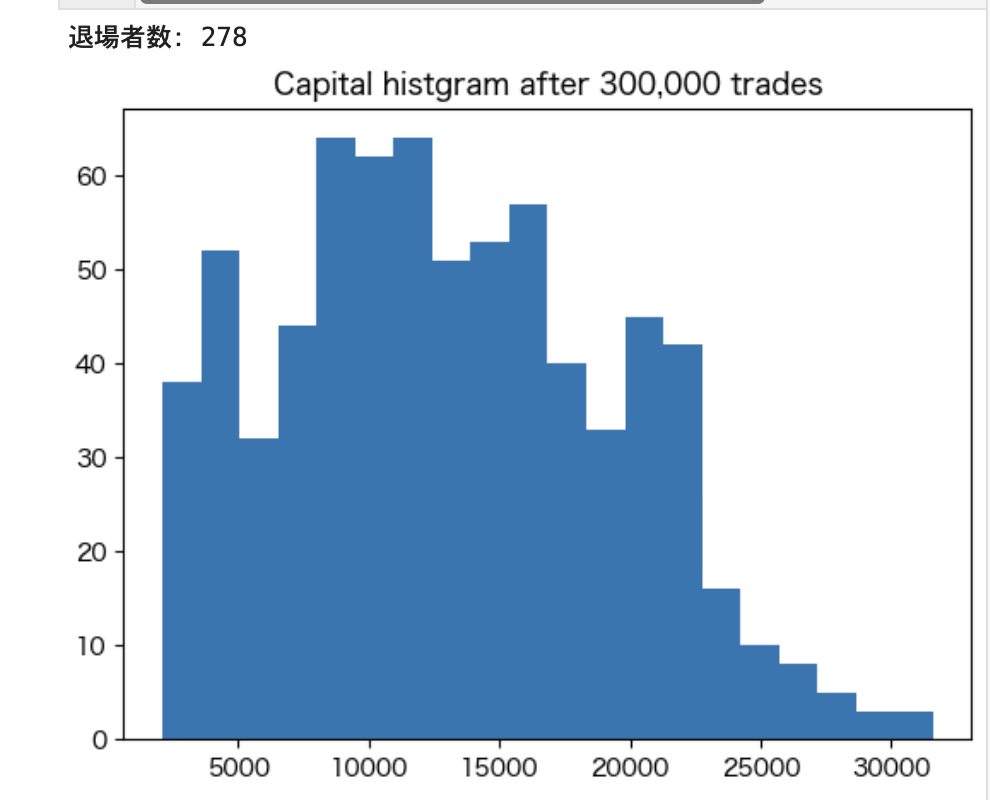
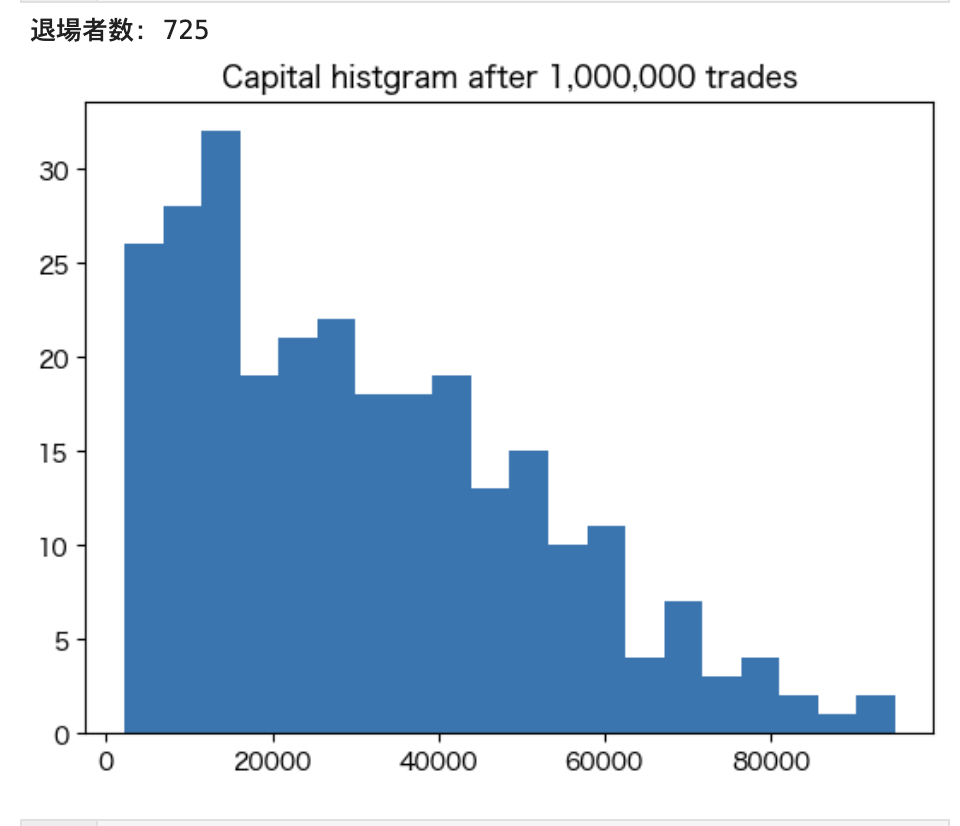
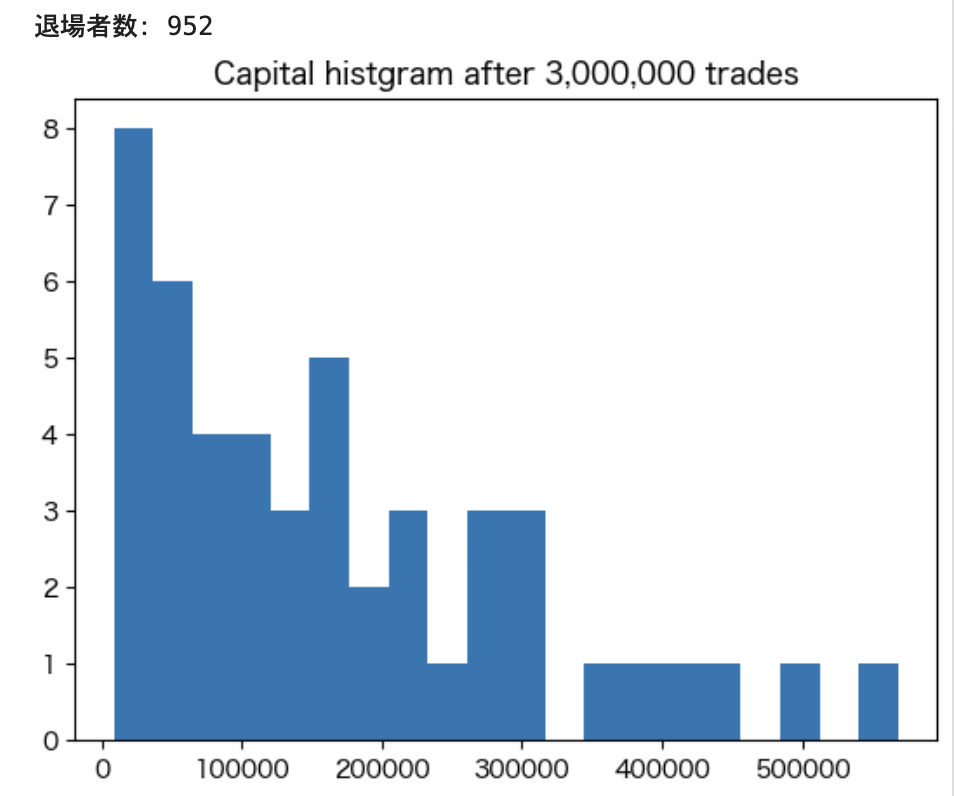
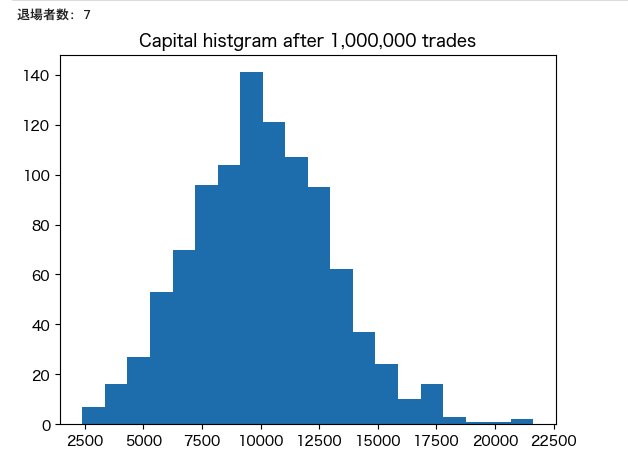
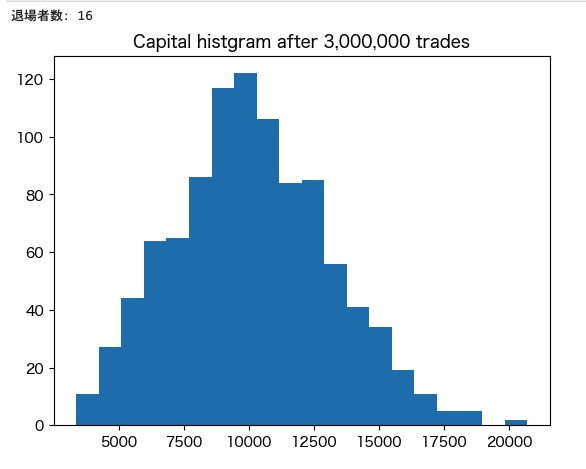
まずは300,000回、1,000,000回、3,000,000回と取引回数を変化させた時の富の分布を見て行きましょう。
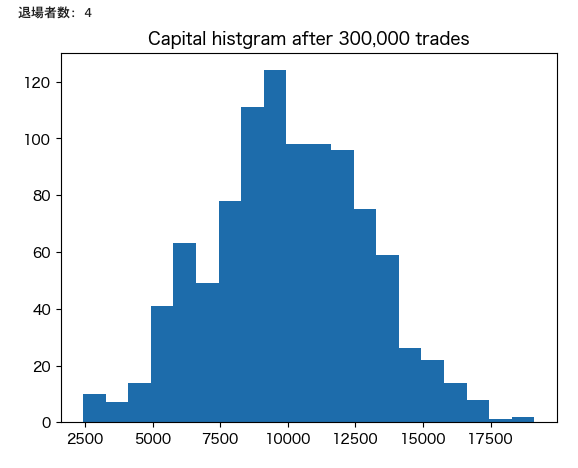
# シミュレーション後の富の分布を見てみる
bins = plt.hist([u.capital for u in result["300000trades"][0]], bins=20)
plt.title("Capital histgram after 300,000 trades")
print("退場者数:", len(result["300000trades"][1]))
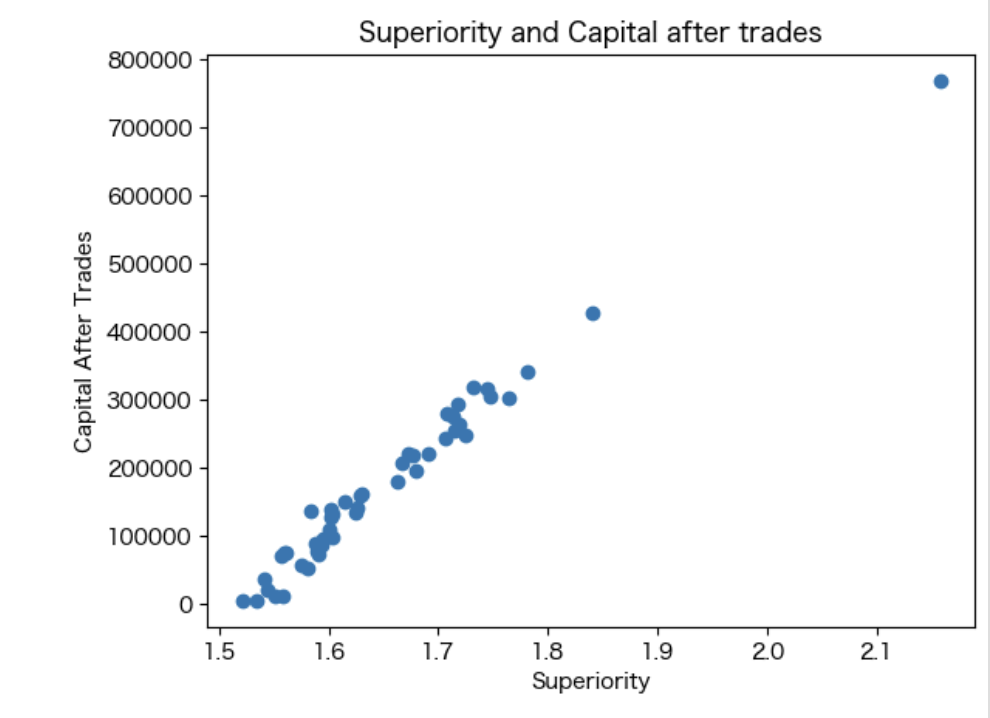
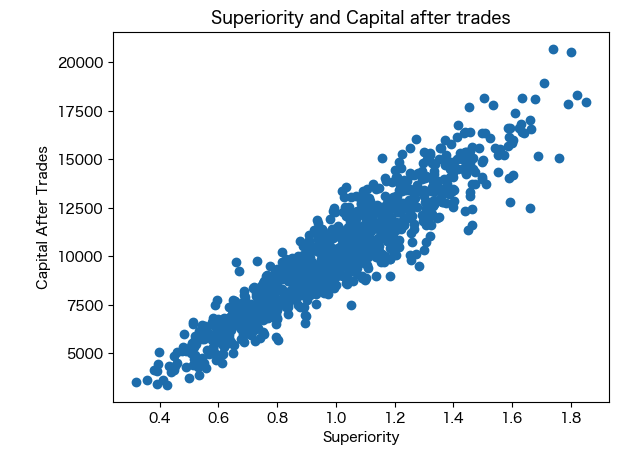
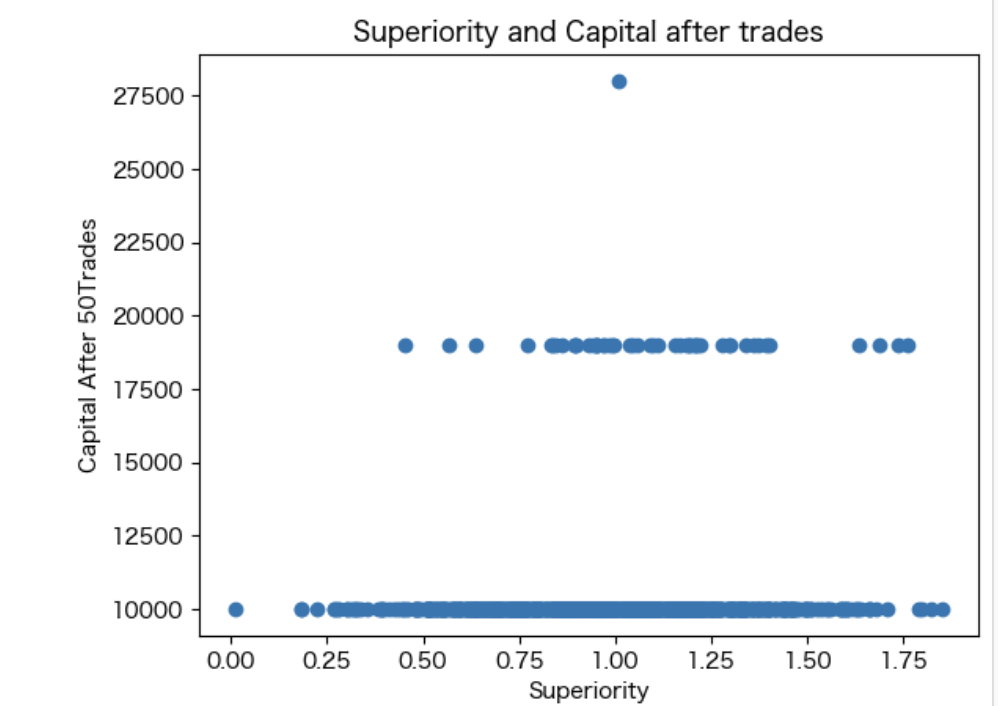
# 富の分布と優位性の散布図
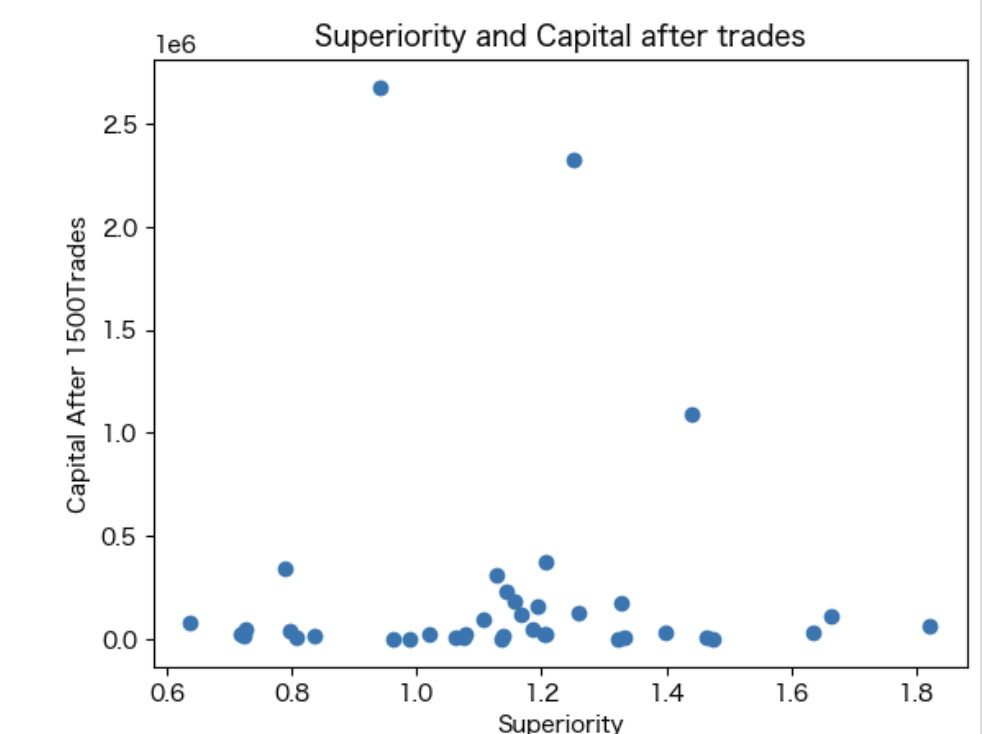
plt.scatter([u.superiority for u in result["3000000trades"][0]], [u.capital for u in result["3000000trades"][0]])
plt.title("Superiority and Capital after trades")
この結果から、次のことがわかります。
- 掛けを定額とすると、取引を繰り返していくことで上位の人たち以外はほぼ全員が退場します
- 具体的には、300万回試行する場合は、9割以上が退場します
- 相対的に上位の人以外は、低い勝率で定額をベットし続けるわけなので当然ではあります
- また、試行を繰り返すごとに、上位の人により極端に富が偏っていくことも分かります
- そして散布図によると、富の分布は市場参加者の持つ優位性と比例しています
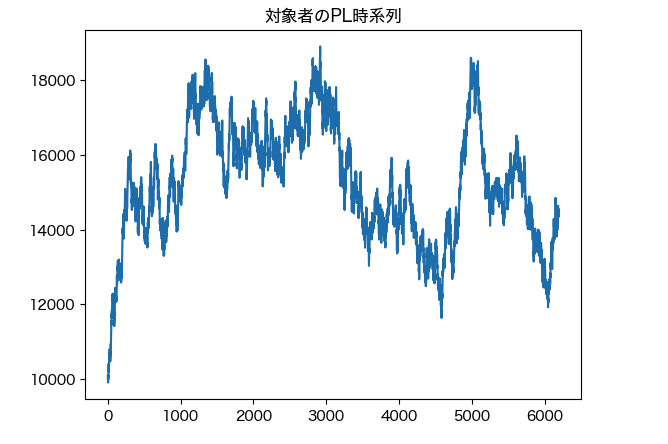
次に、市場参加者のうち、上位30番目(全市場参加者に対して上位0.3%)の優位性を持つ参加者=対象者の富を時系列で可視化してみます。
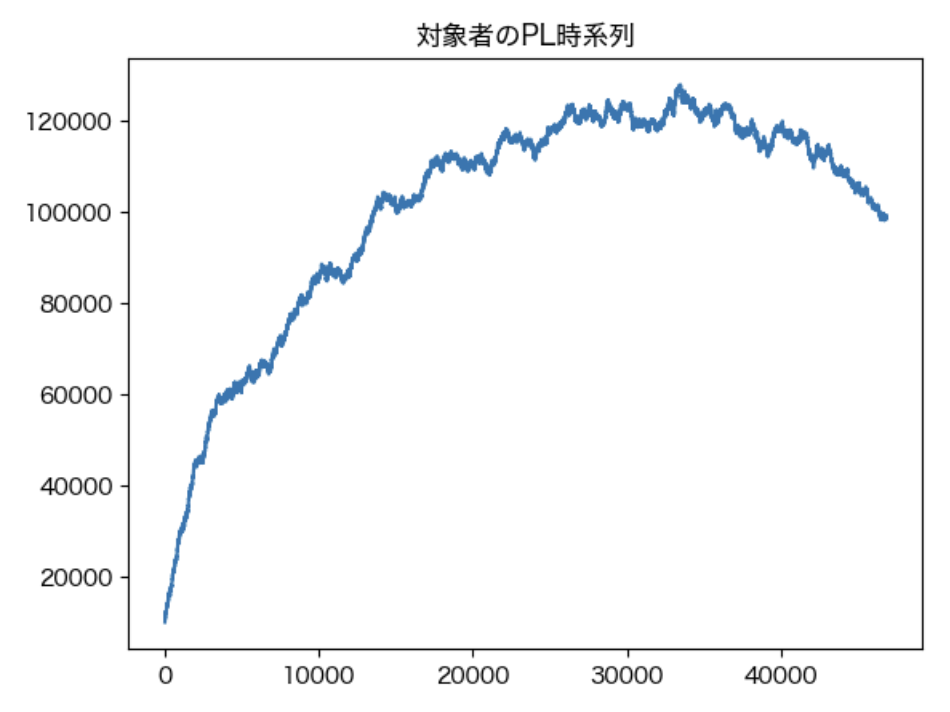
# 損益可視化
u1_result = result["3000000trades"][0][30].capital_history
plt.plot(range(len(u1_result)), u1_result)
plt.title("対象者のPL時系列")
この結果からは次のことが分かります。
- 対象者は市場参加者のうち、自身よりも優位性が低い参加者が多いうちは富を増やし続ける
- しかし、退場者が増えていき、自身よりも優位性が高い参加者が増えていくと、富を増やすことが難しくなっていき、最後には富が減り始める
→ 自身が全市場参加者に対して相対的な優位性を持っていることが、富の増減に影響を与えることがよく分かります
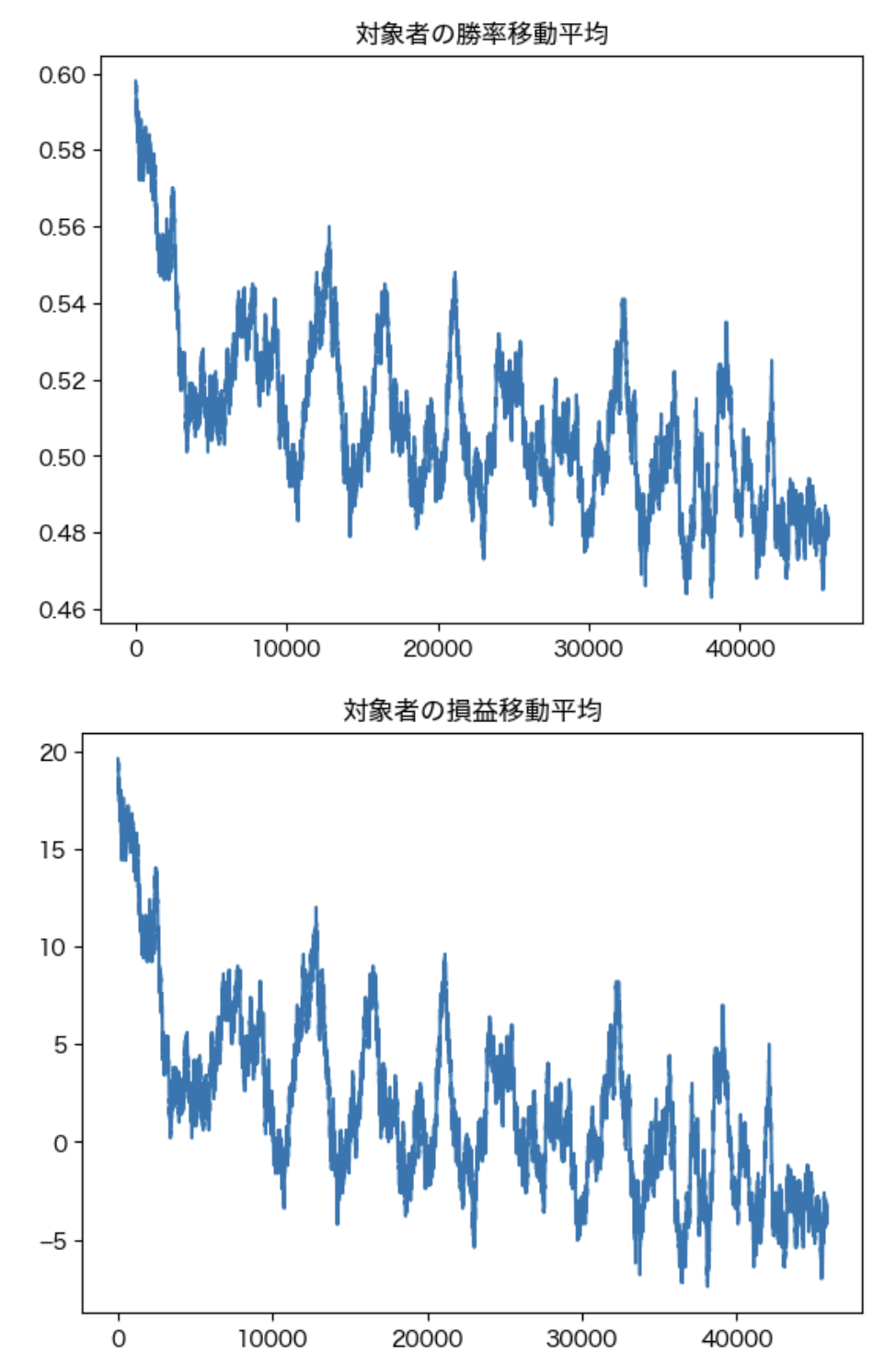
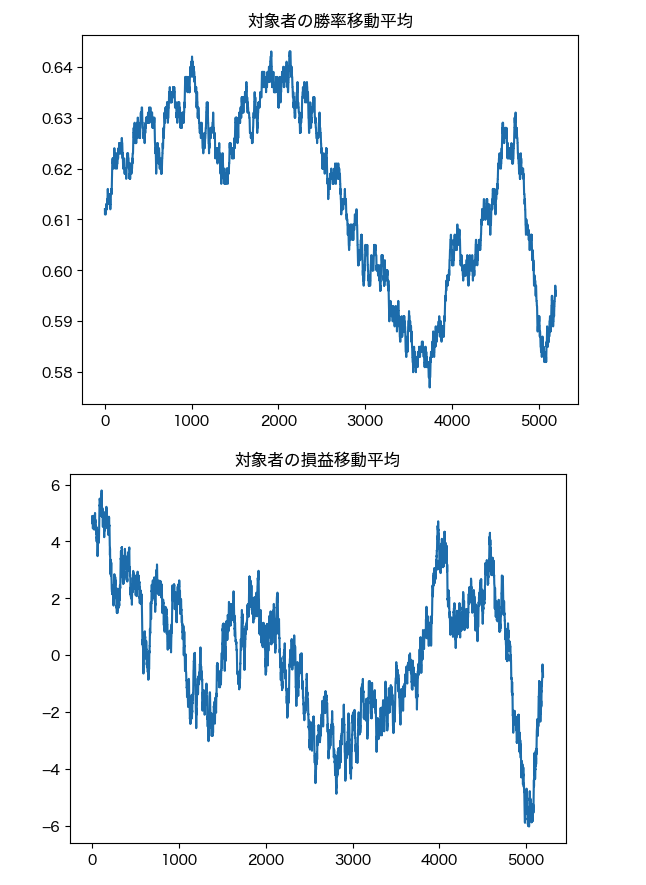
次に、対象者の勝率・損益の移動平均を可視化します。
# 損益の移動平均
u = result["3000000trades"][0][30]
u.calculate_record()
plt.figure()
plt.title("対象者の勝率移動平均")
plt.plot(range(len(u.win_rate_mvavg)), u.win_rate_mvavg)
plt.figure()
plt.title("対象者の損益移動平均")
plt.plot(range(len(u.pl_mvavg)), u.pl_mvavg)
この結果からは次のことが分かります。
- 勝率・平均的なPLが徐々に減少していく。勝率は0.5に、PLは0に近づいていきます
- 勝ち負けの際に移動する金額は200円で固定なので、PLの動きは当然に勝率の動きと一致します
定率で賭ける場合
次のように一部の設定を変更し、定率で賭ける場合のシミュレーションをします。こちらについては、定額で賭ける場合で掲載したグラフをすべて一挙に掲載します。
# 取引を実行する
def trade(users):
u1, u2 = random.sample(users, 2)
u1_bet = u1.bet_capital(0.01) # 定率に変更
u2_bet = u2.bet_capital(0.01) # 定率に変更
p1 = u1.superiority / (u1.superiority + u2.superiority)
p2 = u2.superiority / (u1.superiority + u2.superiority)
winner = np.random.choice([u1, u2], p=[p1, p2])
winner.capital += u1_bet + u2_bet
u1.update_capital()
u2.update_capital()
return u1, u2
- 定率パターンの場合には、試行を繰り返した後の富の分布が、定額と比べて極端ではなくなっていることが分かります
- また、退場者もほとんどいません
→ これは、定率で賭けていく場合、優位性が高い参加者が賭ける額を増やしていく一方で、優位性が低い参加者が賭ける額を減らしていくことで、強い人は勝ったときにより小さく勝ち、弱い人が勝った時はより大きく勝てるためです。
この仕組みにより、次の状態が成り立つ段階で、優位性が低い人から高い人への富の一方的移動が止まります。
強い人の勝率 x 強い人が勝ったときにもらえる金額 = 弱い人の勝率 x 弱い人が勝ったときにもらえる金額
これは、トレードという具体的な対象に当てはめるなら、ロットを上げていくとある段階でそれ以上儲からなくなる現象と同じことと言えます。
なお、ロットの最適化については次のむじネコさん(https://twitter.com/muzineco?ref_src)の記事が面白かったので、皆さんよければ読んでみてください。
定額 / 定率の両シミュレーションから言えること
両シミュレーションから言えることとしては、当たり前のことですが市場全体が大きくならなければ、たとえ強者であろうと富を増やし続けることはできないということだと思っています。
- 定額での賭けの場合、強者であっても最強でなければ、自身がそのうち相対的弱者になることで負けていく
- たとえ最強であっても、最後の1人になった時点でそれ以上富を増やせなくなる
- 定率での賭けの場合、強者であってもある段階で富を増やせない平衡状態になる
このことは、やや話は大きくなりますが、社会全体において、基本的には実力主義で強者が富を増やしていく資本主義社会であっても、社会全体の底上げのために富の再分配が必要なことを裏付けているのではないでしょうか。
また、暗号資産の取引という特定の分野に限って言っても、業界全体を大きくしていなければ、強者も強者で居続けられないでしょう。
自分が弱者だとわかったらどうすれば良いか
さて、ここまで相対的強者であることが重要という話をしました。では自分がその集団の中で相対的弱者であることを自覚している場合にはどういった行動を取ればいいのでしょうか。
筆者としては、自身の能力に対して最大限富を増やす方法として、次の2つの選択肢のいずれかを取るべきであると考えています。
- そもそも競争に参加しない(自分が相対的強者になれる次の市場が現れるのを待つ)
- 試行回数が少なく、1回あたりの富の動きが大きい競争に、損失覚悟で参加する
1については直感的でわかりやすいですが、2についてはやや分かりづらいので、次のような設定で実験をした結果を掲載します。
- 基本的には上記のシミュレーションを実行する
- 試行回数は50回、1500回の2パターン
- 参加者は1回の試行で富の90%を賭ける
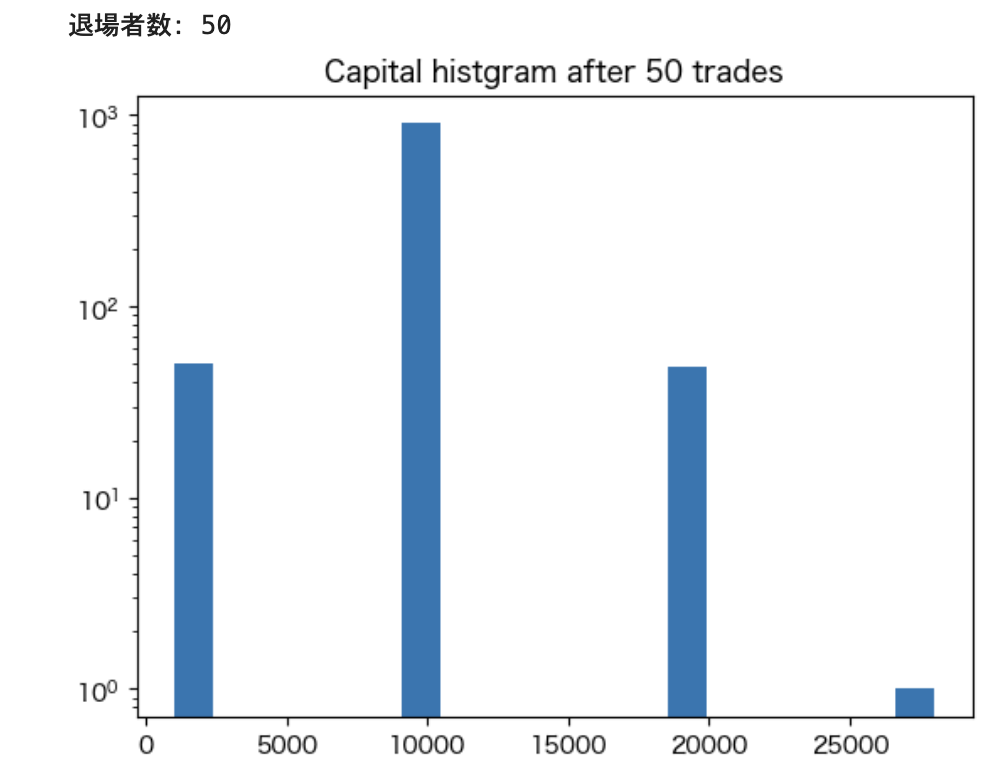
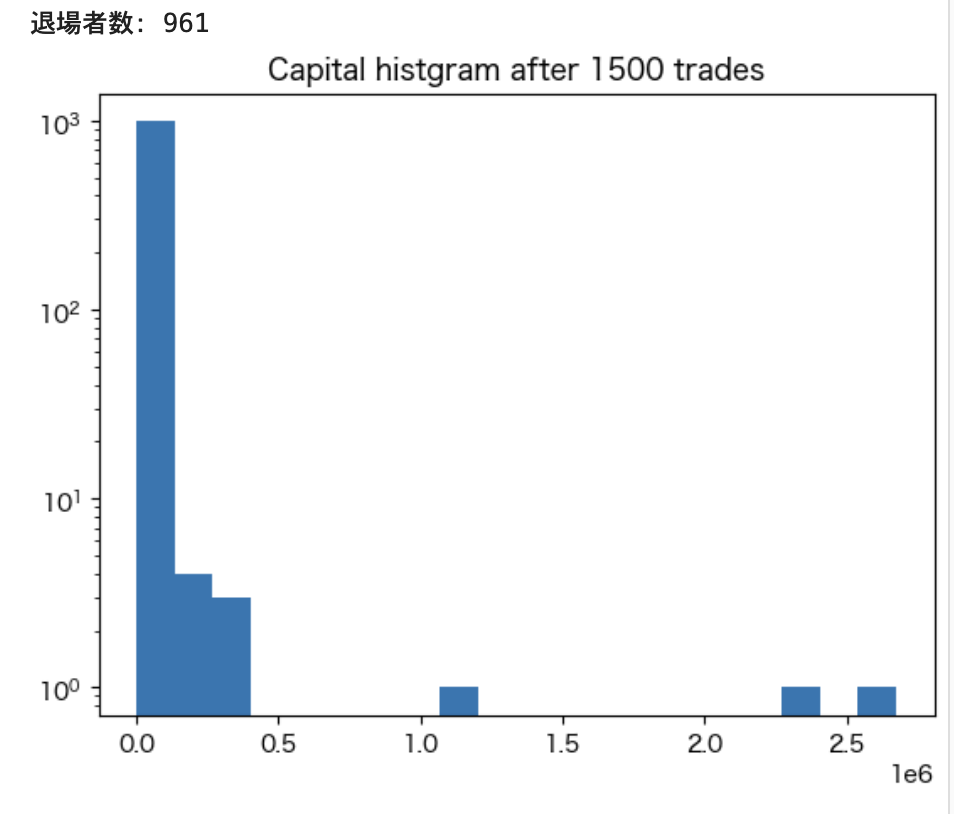
この実験から分かることは次です。
- 試行回数が少ない(50回)の場合、優位性が低い者でも富を2倍にできている参加者がいる
- 試行回数が増えると、ほぼ全員が退場する
つまり、富の大部分を1度に賭けるような試行においては、能力よりも運が重要であり、試行回数を重ねると基本的には破産することになります。
そのため、弱者である自覚がある人としては、運によって勝った後に、試行回数が少なく破産確率が低いうちに勝ち逃げするという戦略が有効であることになります。
なお、2の選択肢ははっきり言って運任せの丁半博打であり、おすすめはできません。
ちなみに自分自身が相対的に弱者であることを自覚していない弱者については、かなり厳しく、成果を出すことが難しいと言わざるを得ません。自身の能力が相対的に低いことを指摘されると、怒ったり悲しんだりというような感情的な反応をする人がそれにあたります。
何かしらの分野について能力が低いというのは、単なる事実にすぎず、そこに良い悪いなどという解釈はないのですが、それを指摘されて感情的になっているということは、その事実を受け入れられていないことになります。
上記のような弱者の戦略は、自身が弱者であることを自覚して始めて取れる行動ですから、自覚のない弱者というのはそれ以前の段階ということになります。
参考:シミュレーションを行う意味について
なお、今回のシミュレーション結果については、別に新しい発見というわけではなく、「そういう設定でシミュレーションをしたからそういう結果が出た」というものに過ぎません。
よって、結果自体もシミュレーションをする前から分かっていたものではあります。しかし、現実に起きていることを抽象化し、そのシミュレーション結果をうまく可視化することで、現実の理解をより解像度高くできると考えています。
より現実に近づけるなら、新規で市場に参入する人が確率的に現れるようなモデルとすることや、ベットする額の決定にランダム性や市場参加者ごとのリスク選好度を盛り込むこともできると思います。
最後に
この記事では、bot業界の歴史や必要とされるスキルセットを振り返りながら、簡単なシミュレーションによって次のことを示しました。
- ベットする富が十分に小さい場合には、能力が相対的に高いことが勝つために重要であり、能力の絶対値が高くても、周囲の能力が高いと負けてしまう
- 自身が弱者であることに自覚的であるならば、そもそも勝負に参加しないか、一か八かの大勝負を挑むことが有効な戦略となる
bot取引がこの3-4年で非常に市民権を得ている感がありますが、個人的にはbot取引のような知力・技術力勝負が得意でないと自覚しているのならば、苦手な分野に挑戦しない、市場に参加しないというのが最適解だと思っています。
筆者がbot取引を始めたのは20代前半の頃ですが、今となっては20代後半にも差し掛かり、世の中にはいろいろな魅力・能力がある人がたくさんいることを、実感としてよく理解できてきました。そういった魅力を持っている人が、SNSに煽られて偶然に始めてしまった、向いていないbot取引で消耗するのはもったいないと思いますし、お金を稼ぐという目的なら、それぞれの能力を活かしてできることが、想像以上に多分野でたくさんあるはずです。
そして筆者としてはそもそも、お金を稼ぐことが本当に目的なのかというのもよく考えた方がいいと思っており、個人的にはお金が大量にあることよりも、お金にしろ何にしろ一定の制約の中で工夫することも含めて、その過程を楽しめる友人や家族がいることの方が、人生の幸福度が高くなりやすいのではないかと考えています。
それでは最後になりますが、クリスマスの日に愛を込めてこの言葉を贈ります。
#botは儲からないからやめた方がいい
追伸
- 最近Twitterアカウントの名前を変えることを考えています。スナフキンという名前がそろそろ恥ずかしくなってきました。良い名前を募集中です!
- ぼくの働いているCoincheckでは、引き続きエンジニアを中心に採用活動を行っています。暗号資産は冬の時代ですが、DEX botterの方々からのご応募もお待ちしています!