はじめに
計測した時間信号が,周波数領域においてどのような特徴(固有振動数・次数音など)を持っているのか?を調べる際に用いられる信号処理手法の1つである**FFT(高速フーリエ変換)**のプログラムコードをここで共有させていただきます.
前置き
・基本概念は,他の方が解説して頂いたので省きます.
・これが初めての投稿となるので,温かい目で見守っていただけるとありがたいです.
・PyCharm 2020.3.2 (Community Edition)
目的
今まで拝見した記事の中では,横軸を周波数 [Hz],縦軸を音圧レベル [dB]または騒音レベル [dBA] としたグラフは見られませんでした(調査不足なだけ).なので,今回は [dB] による周波数分析を試みます.
解析対象のデータのFFT条件
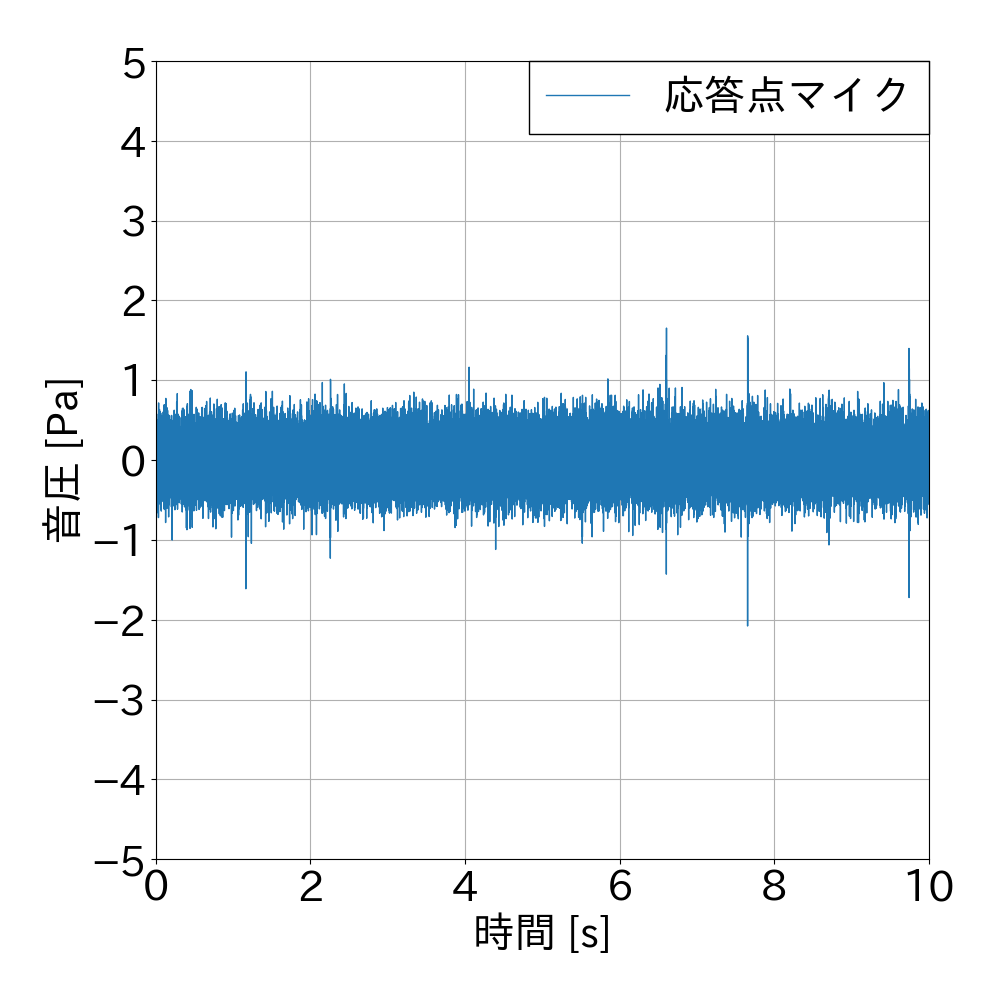
・解析対象は,ホワイトノイズ環境下で外壁タイルを1秒間に1回の頻度で10秒間加振した時の打音データです.
・サンプリングレート fs:8192 Hz
・FFTブロックサイズ block_size:8192 点
・オーバーラップ overlap:0.75
・周波数分解能 df:1.0 Hz
・1回のFFTにかかる時間:1.0 sec
・打音計測マイクのチャンネル本数:1 ch
import類
import numpy as np # 数値演算ライブラリ
import matplotlib.pyplot as plt # 描画ライブラリ
import japanize_matplotlib # グラフの軸ラベルや凡例などを日本語化
import scipy.integrate as si # 積分
import scipy.signal as ss
import sympy as sp # FFT条件を設定した後,何回FFTしないといけないか計算するために必要
FFTコード
def fft(data, fs, block_size, output_ch, overlap):
max_frequency = fs / 2.56 # 上限解析周波数
line_number = block_size / 2.56 # ライン数
df = max_frequency / line_number # 周波数分解能
dt = 1 / fs
block_size_range = np.arange(0, block_size, 1)
nf = np.int((fs / 2) + 1) # ナイキスト周波数
nf_line = (block_size_range / (dt * block_size))[:nf] # 周波数軸
impact_time_data = data[:, 0] # 力センサが取り付けられたハンマの時間波形(インパルス入力)
output_time_data = data[:, 1] # 応答点マイク(打撃音計測専用マイク)
time_line = np.arange(0, data.shape[0] / fs, dt) # 時間軸
# def time_graph():
# plt.rcParams['font.size'] = 30
# plt.figure(figsize=(10, 10))
# plt.plot(time_line, output_time_data, label='応答点マイク', linewidth=1, color='C1')
# plt.ylabel('音圧 [Pa]')
# plt.xlabel('時間 [s]')
# plt.xlim(0, 1)
# plt.ylim(-5, 5)
# plt.yticks(np.arange(-5, 6, 1))
# plt.grid(True)
# plt.legend(loc="upper right", borderaxespad=0, edgecolor='black', framealpha=1, fancybox=False)
# plt.tight_layout()
#
# plt.figure(figsize=(10, 10))
# plt.plot(time_line, impact_time_data, label='加振ハンマ', linewidth=1, color='C2')
# plt.xlabel('時間 [s]')
# plt.ylabel('力 [N]')
# plt.xlim(0, 1)
# plt.ylim(0, 50)
# plt.grid(True)
# plt.legend(loc="upper right", borderaxespad=0, edgecolor='black', framealpha=1, fancybox=False)
# plt.tight_layout()
# time_graph()
"iteration計算"
n = sp.Symbol('n')
right = 0 + (n - 1) * block_size * (1 - overlap)
left = data.shape[0] - block_size
zero = right - left
iteration = np.int(sp.solve(zero)[0])
"FFT開始地点"
start_point = [
np.int(0 + (i - 1) * block_size * (1 - overlap))
for i in range(1, iteration + 1)
]
output_use = [
np.reshape(output_time_data[start_point[i]:start_point[i] + block_size], (block_size, output_ch))
for i in range(iteration)
]
"簡易積分"
def hanning_integral():
global hanning_simpson
hanning_simpson = si.simps(np.hanning(block_size), dx=1 / fs)
hanning_correction = 1 / hanning_simpson
print('hanning_windowの欠損率は {0}'.format(hanning_simpson))
print('だから,相対的に {0} 倍する必要がある'.format(hanning_correction))
return hanning_correction
hanning_window_correction = hanning_integral()
"厳密解"
def exact_solution(x):
hanning_formula = 0.5 - 0.5 * sp.cos(2 * np.pi * x)
return hanning_formula
global hanning_integration
hanning_integration = si.quad(exact_solution, 0, 1)
print('厳密解 {0} '.format(1 / hanning_integration[0]))
# FFT
output_fft = [
[
((np.fft.fft(np.hanning(block_size) * output_use[i][:, j])[:nf]) /
block_size) * (2 * 1 / hanning_integration[0])
for i in range(iteration)
]
for j in range(output_ch)
]
'--------------------行列サイズの変換(FFT繰り返し数×応答点のチャンネル数)--------------------'
output_reshape1 = [
np.reshape(output_fft[j], (iteration, nf))
for j in range(output_ch)
]
output_reshape2 = [
[
output_reshape1[j][:, k]
for j in range(output_ch)
]
for k in range(nf)
]
output_reshape3 = [
np.reshape(output_reshape2[k], (output_ch, iteration)).T
for k in range(nf)
]
'--------------------音圧レベル--------------------'
output_dB = [
20 * np.log10(np.sqrt(np.mean(np.power(np.abs(output_reshape3[k]), 2), axis=0)) / 2e-5)
for k in range(nf)
]
output_dB = np.reshape(output_dB, (nf, output_ch))
# def fft_graph():
# plt.figure(figsize=(10, 10))
# plt.plot(nf_line, output_dB, color='C0', linewidth=3, label="応答点")
# plt.xlim(0, 2000)
# plt.xticks(np.arange(0, 2200, 200))
# plt.axvspan(1020, 1100, color='green', alpha=0.3)
# plt.ylim(0, 80)
# plt.yticks(np.arange(0, 90, 10))
# plt.xlabel('周波数 [Hz]')
# plt.ylabel("音圧レベル [dB]")
# plt.grid(True)
# plt.legend(loc="upper right", borderaxespad=0, edgecolor='black', framealpha=1, fancybox=False)
# plt.tight_layout()
# pass
#
# fft_graph()
return output_reshape3, nf, nf_line, output_dB, iteration, fs, block_size, output_ch, overlap
各パーツごとの解説
iteration計算(FFT繰り返し数)
オーバーラップを設定した場合,FFTは複数回連続して行なうことになりますが,何回FFTしないといけないのかは自分で計算する必要があります.
今回計測された音圧信号のデータ数は81920個(サンプリングレート×計測時間)存在します.
オーバーラップ75 %ということは,1回目のFFT開始地点から,FFT 1 ブロックの25 %ずらしたことと同じ意味ですよね?(下図)
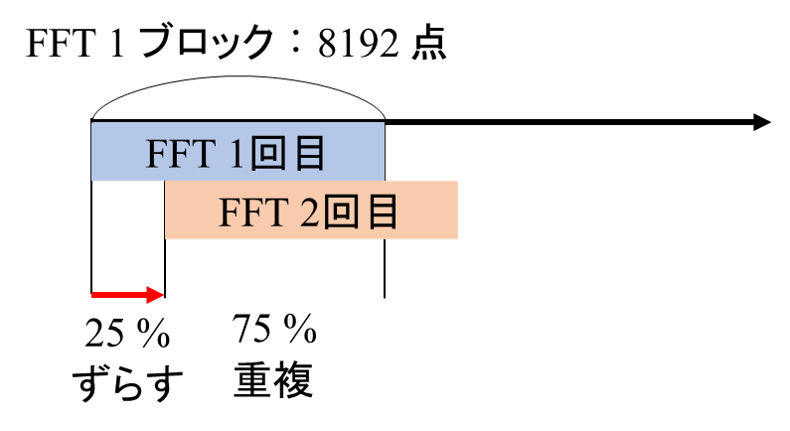
ということは,繰り返しFFTをする際のスタート地点は,初項が0(PythonだからIndexが0番から始まる),交差が2048(8192 点×0.25)の等差数列として扱えませんか?
$$
a(n) = 0 + (n-1)blocksize(1-overlap)(nがFFTの繰り返し数.これが知りたい!)
$$
この式が,プログラムコードの「right」部分になります.
しかしながら,この等差数列だけではFFT繰り返し数は求められません!
そうです.いつ等差数列が終わるのか?という情報が必要になります.
そこで,最後にFFTするときのFFT開始地点を考えてみましょう.
最後にFFTするときは,データのインデックスが73728番(81920 - 8192)の時ですね.
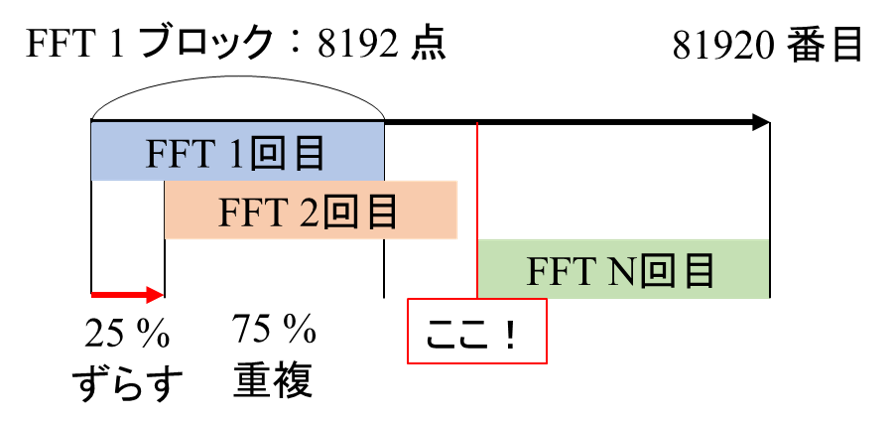
この73728番目の時のnを求めると,FFT繰り返し数が分かります.
$$
0 + (n-1)blocksize(1-overlap) = 全データ数 - blockszie
$$
ここの式が,プログラムコードの「left」部分になります.
$$
iteration = n = \frac{全データ数 - blocksize×overlap}{blocksize(1 - overlap)}
$$
ウィンドウ関数で生データがどれほど振幅欠損するか?
ここでは,補正量の計算について説明しています.
ハニングウィンドウをかけることで,FFT 1 ブロックの両端は必ず0になり,リーケージエラーを防ぐことができます.このメリットに対して,無理矢理信号を変えたわけですから,その分補正し返してあげる必要があります.ここでウィンドウ関数をかけなかった時とハニングウィンドウをかけた時の面積を計算してみましょう.
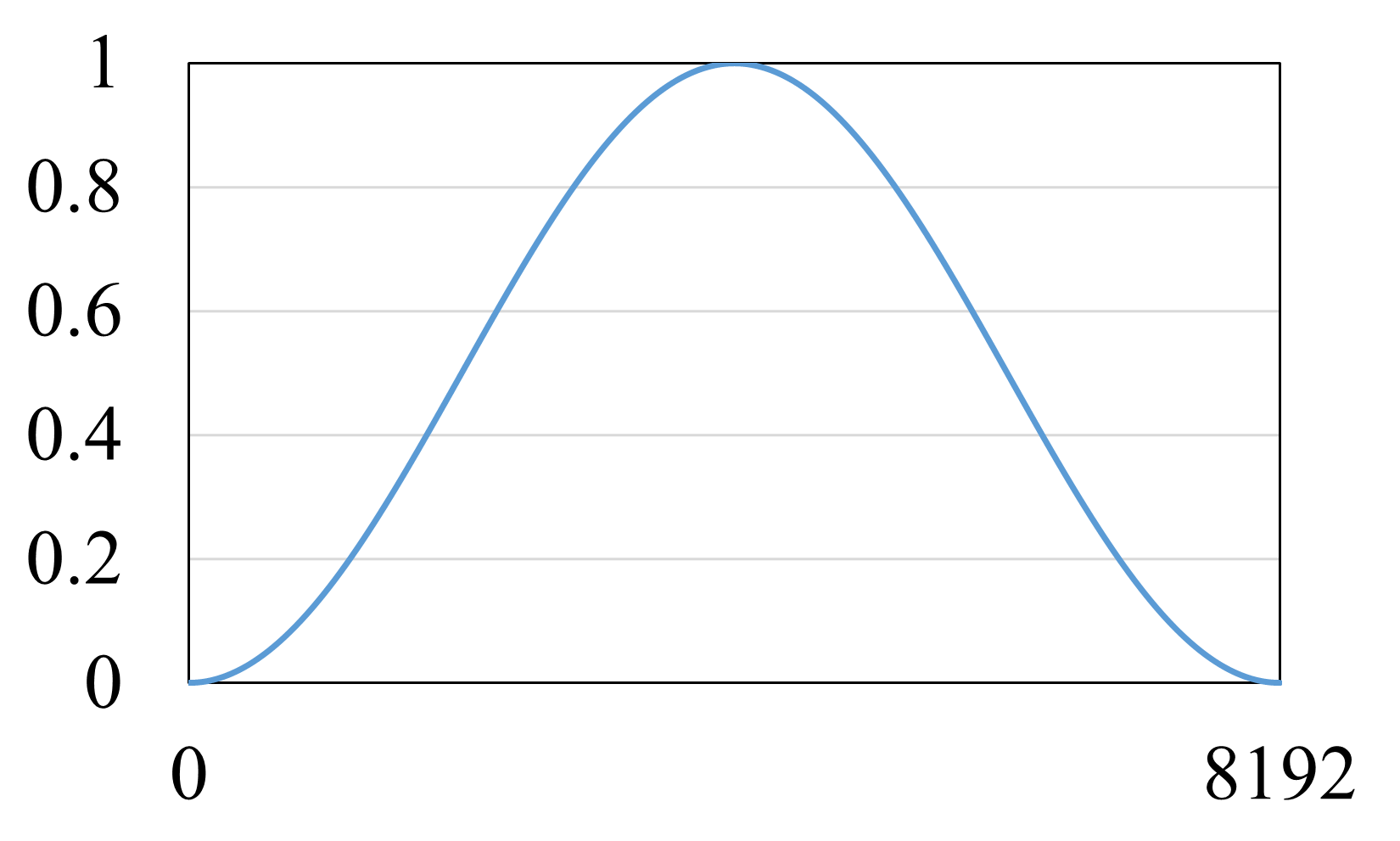
面積は,ハニングウィンドウの線よりも下の領域になります.ですので,面積はウィンドウを何も書けない時に比べて
hanning_simpson = si.simps(np.hanning(block_size), dx=1 / fs)
これだけ小さくなります.ですので,小さくなった分補正し返す(要は逆数をかける)必要があります.
関数呼び出し
noise_impact_output_ffts, nf, nf_line, noise_impact_output_ffts_dB, ffts_iteration, fs, block_size, output_ch, overlap = fft(data=noise_impact, fs=8192, block_size=8192, output_ch=1, overlap=0.75)
得られた結果
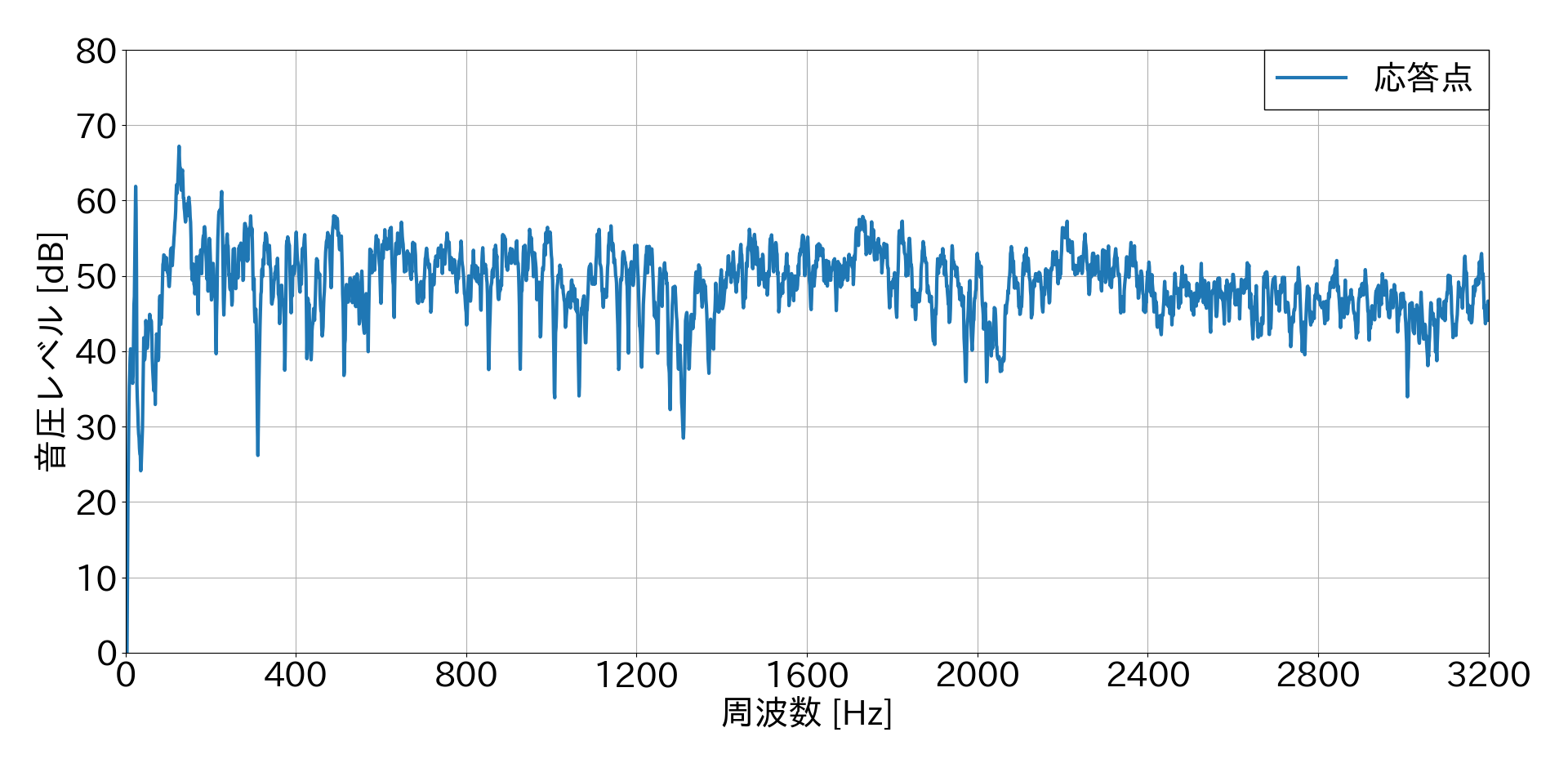
ホワイトノイズ+打音データをFFTすると,このような結果が得られました.本来であれば,打音の共振点が図に現れるはずなのですが,今回のホワイトノイズ環境下で加振した場合,打音成分はノイズに埋もれてしまったと考えられます.(静粛環境下で加振したデータを解析対象にすればよかったですね...)また,共振周波数に着目せずとも,全周波数で約50 dBの一定した信号でもあることが見て取れます.したがって,ホワイトノイズの特徴とも一致します.
なお,今回は全データを用いてFFTを行ないましたが,打音は一瞬なので,力が入力された瞬間周辺1秒をトリミングしてからFFTすべきです.(別の記事に書きます.)
いかがでしたか?
ここまで読んで頂き誠にありがとうございました.今回は,人間の聴覚特性を考慮したdB表記の周波数分析を試してみました.この記事が誰かの助けになれば幸いです.
修正事項
タグ名変更(Python3➡Python)