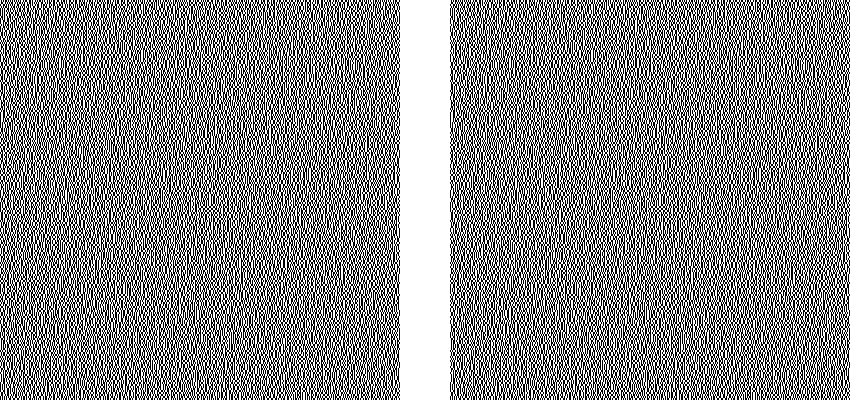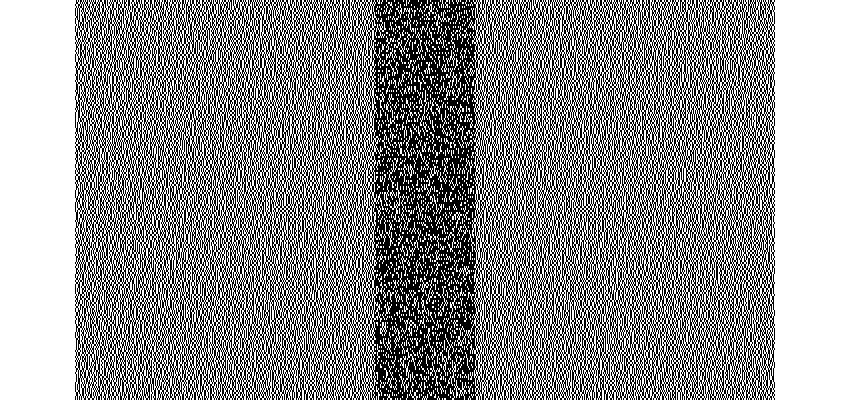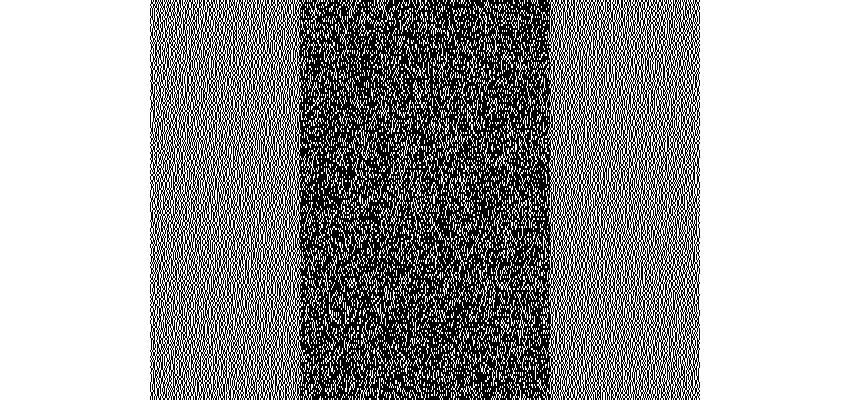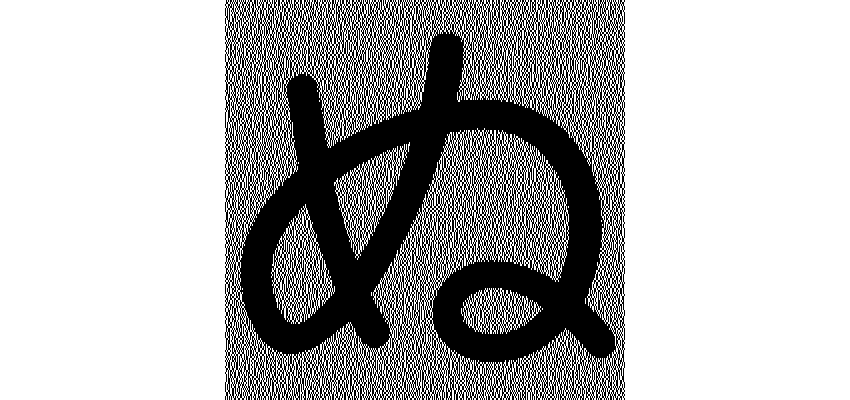視覚復号型秘密分散法 理論編

はじめに

前回の記事ではシャミアの秘密分散法の理論と実装の説明をしました。

今回は、視覚復号型秘密分散法と呼ばれる秘密分散法の説明をしていきます。

視覚復号型秘密分散法

計算機を使うことなく再構成を行えるような秘密分散法があり、その中でも視覚を用いることで再構成が行える秘密分散法のことを、視覚復号型秘密分散法と言います。

視覚復号型秘密分散法における、秘密情報は画像ですが、画像はピクセルの集合なので、一つのピクセルの色の情報を秘密情報として扱えばよいです。
そのため、ここからは一つのピクセルの情報をどのように分散するかについて説明していきます。
またこの記事では、最も一般的なバイナリ画像の視覚復号型秘密分散法を説明するので、扱う色は白と黒の二色のみです。

視覚複合型秘密分散法の基本的なアイデアは、秘密情報である一つのピクセルを、シェアとして複数のピクセルに分けるというものです。
分けた複数のピクセルのことをサブピクセルといい、これらを重ね合わせたとき、元のピクセルの情報が浮かび上がるようにします。
以下の画像を参照すると、分かりやすいと思います。

秘密情報が黒のときと白のときで、再構成されたピクセルの黒(白)の個数が異なるようにします。
つまり、ある整数 $\alpha$ に対して、
秘密情報が白であれば、再構成されたピクセルでは黒の個数が $\alpha$ 未満となり、
秘密情報が黒であれば、再構成されたピクセルで黒の個数が $\alpha$ 以上となるようにします。
こうすることで、最初にあげた画像のように、人の目でも、相対的に色の判断をすることができます。

まず $(2, 2)$ 視覚復号型秘密分散法を説明し、次に $(3, 4)$ 視覚復号型秘密分散法を説明します。

(2, 2) 視覚復号型秘密分散法

最初に、シェアの生成方法・再構成の方法を説明し、その後それらが暗号学的に問題ないことを証明します。

シェアの生成

まず、二つの行列 $C_0, C_1$ を以下のように定義します。

\begin{align}
C_0 &= 
\begin{pmatrix}
0 & 1 \\
0 & 1
\end{pmatrix} \\
C_1 &= 
\begin{pmatrix}
0 & 1 \\
1 & 0
\end{pmatrix}
\end{align}

そして、以下のようにして参加者にシェアを渡します。

• 秘密情報となるピクセルが白のとき
  1. $C_0$ の列をランダムに入れ替えたものを $C_0'$ とする
  2. 1 人目の参加者に $C_0'$ の 1 行目を渡す
  3. 2 人目の参加者に $C_0'$ の 2 行目を渡す
• 秘密情報となるピクセルが黒のとき
  1. $C_1$ の列をランダムに入れ替えたものを $C_1'$ とする
  2. 1 人目の参加者に $C_1'$ の 1 行目を渡す
  3. 2 人目の参加者に $C_1'$ の 2 行目を渡す

これによって、各参加者は 1 行 2 列の行列をシェアとして受け取ります。
この行列がサブピクセルとなり、0 となっている場所を白色、1 となっている場所を黒色とします。

秘密情報の再構成

シェアの行列を、要素毎の論理和によって、再構成をします。

例えば、1人目の参加者が $\begin{pmatrix} 1 & 0 \end{pmatrix}$ を持っていて、2 人目の参加者が $\begin{pmatrix} 0 & 1 \end{pmatrix}$ を持っている場合、これらで再構成を行うと、

\begin{align}
\begin{pmatrix} 1 & 0 \end{pmatrix} \vee \begin{pmatrix} 0 & 1 \end{pmatrix}
&= \begin{pmatrix} 1 \vee 0 & 0 \vee 1 \end{pmatrix} \\
&= \begin{pmatrix} 1 & 1 \end{pmatrix}
\end{align}

となります。
シェアから分かるように元の秘密情報は黒で、全ての要素が 1 になっているので、再構成後も黒一色になっていることが分かります。

また、シェアの生成方法と再構成の方法から、再構成された行列の要素における 0/1 の個数は、秘密情報のみに依存します。
つまり、以下のようになります。

• $C_0$ からシェアを生成して再構成した場合
  • 0 となる要素数: 1 個
  • 1 となる要素数: 1 個
• $C_1$ からシェアを生成して再構成した場合
  • 0 となる要素数: 0 個
  • 1 となる要素数: 2 個

今回の方法の場合、元の情報が白のときより黒のときの方が、再構成したときの黒の個数が多くなるので、人の目で再構成できることが分かります。

ちなみに、サブピクセルのサイズが 1 行 2 列なので、再構成すると画像が横に長くなります。

安全性の証明

秘密情報が白の場合、$C_0'$ は以下の 2 通りになります。

\begin{pmatrix}
0 & 1 \\
0 & 1
\end{pmatrix}
, \;
\begin{pmatrix}
1 & 0 \\
1 & 0
\end{pmatrix}

これより、参加者はそれぞれ $\dfrac{1}{2!}$ の確率で $\begin{pmatrix} 0 & 1 \end{pmatrix}, \; \begin{pmatrix} 1 & 0 \end{pmatrix}$ をシェアとして渡されます。
また、秘密情報が黒の場合、$C_1'$ は以下の 2 通りになります。

\begin{pmatrix}
0 & 1 \\
1 & 0
\end{pmatrix}
, \;
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}

これより、参加者はそれぞれ $\dfrac{1}{2!}$ の確率で $\begin{pmatrix} 0 & 1 \end{pmatrix}$, $\begin{pmatrix} 1 & 0 \end{pmatrix}$ をシェアとして渡されます。

逆に、シェアが $\begin{pmatrix} 0 & 1 \end{pmatrix}$ のとき、秘密情報の色が白である確率も、黒である確率も $\dfrac{1}{2}$ なので、シェアからは情報が漏れていないことが分かります。
シェアが $\begin{pmatrix} 1 & 0 \end{pmatrix}$ のときも、同じようにして情報が漏れていないことが分かります。
これ以外にシェアとなりうる行列は無いので、シェアが 1 つしか集まっていない場合、つまりシェアが 2 つ未満の場合、秘密情報が漏れることはなく、安全であることが証明できました。

(2, 2) 視覚復号型秘密分散法の実例

画像を載せているだけで、少し長いので折りたたんでいます。

実際の例

• 秘密情報
  

• シェア画像

1 つ目	2 つ目

• シェアから再構成した秘密情報
  

(3, 4) 視覚復号型秘密分散法

$(2, 2)$ のときと同様に進めていきます。

まず、二つの行列 $C_0, C_1$ を以下のように定義します。

\begin{align}
C_0 &= 
\begin{pmatrix}
0 & 0 & 0 & 1 & 1 & 1 \\
0 & 0 & 1 & 0 & 1 & 1 \\
0 & 0 & 1 & 1 & 0 & 1 \\
0 & 0 & 1 & 1 & 1 & 0
\end{pmatrix} \\
C_1 &= 
\begin{pmatrix}
1 & 1 & 1 & 0 & 0 & 0 \\
1 & 1 & 0 & 1 & 0 & 0 \\
1 & 1 & 0 & 0 & 1 & 0 \\
1 & 1 & 0 & 0 & 0 & 1
\end{pmatrix}
\end{align}

そして、以下のようにして参加者にシェアを渡します。
この部分は、一般的な $(k, n)$ の場合でも変わりません。

• 秘密情報となるピクセルが白のとき
  1. $C_0$ の列をランダムに入れ替えたものを $C_0'$ とする
  2. $i$ 人目の参加者に $C_0'$ の $i$ 行目を渡す ($1 \leq i \leq 4$)
• 秘密情報となるピクセルが黒のとき
  1. $C_1$ の列をランダムに入れ替えたものを $C_1'$ とする
  2. $i$ 人目の参加者に $C_1'$ の $i$ 行目を渡す ($1 \leq i \leq 4$)

これによって、各参加者は 1 行 4 列の行列をシェアとして受け取ります。

秘密情報の再構成

再構成の方法も $(2, 2)$ のときと同様に、要素毎の論理和をとります。

また、再構成された行列の要素における 0/1 の個数は、以下のようになります。

• 3 つのシェアから再構成する場合
  • $C_0$ からシェアを生成して再構成した場合
    • 0 となる要素数: 2 個
    • 1 となる要素数: 4 個
  • $C_1$ からシェアを生成して再構成した場合
    • 0 となる要素数: 1 個
    • 1 となる要素数: 5 個
• 4 つのシェアから再構成する場合
  • $C_0$ からシェアを生成して再構成した場合
    • 0 となる要素数: 2 個
    • 1 となる要素数: 4 個
  • $C_1$ からシェアを生成して再構成した場合
    • 0 となる要素数: 0 個
    • 1 となる要素数: 6 個

今回の方法の場合も、元の情報が白のときより黒のときの方が、再構成したときの黒の個数が多くなるので、人の目で再構成できることが分かります。

ちなみに、サブピクセルのサイズが 1 行 6 列なので、再構成すると画像がかなり横に長くなってしまいます。
しかし、2 行 3 列等に並べなおすことで、多少抑制することもできます。

安全性の証明

$(2, 2)$ のときと、同じような証明をしようと思うと、通り数がかなり多くなってしまうので、少し違う方法で安全性の証明をしていきます。

まず $C_0$ や $C_1$ を行毎に見たとき、常に 0 と 1 は 3 個ずつになります。
したがって、各参加者には $\dfrac{6!}{3!3!}$ 通りの内から、等確率でシェアが渡されます。
よって、シェアが 1 つの場合、いかなる情報も漏れないことが分かります。

そして、$C_0$ の中から任意の 2 行を選んだとき、現れる列は以下のような分布になります。

• $\begin{pmatrix}0 \\ 0\end{pmatrix}$ となる列数: 2列
• $\begin{pmatrix}0 \\ 1\end{pmatrix}$ となる列数: 1列
• $\begin{pmatrix}1 \\ 0\end{pmatrix}$ となる列数: 1列
• $\begin{pmatrix}1 \\ 1\end{pmatrix}$ となる列数: 2列

$C_1$ のときも同様に調べると、全く同じ分布になります。
したがって、シェアが 2 つ集まっている場合、いかなる情報も漏れないことが分かります。

上記より、シェアが 3 つ未満の場合、いかなる情報も漏れないことが証明されました。

(3, 4) 視覚復号型秘密分散法の実例

画像を載せているだけで、少し長いので折りたたんでいます。
サブピクセルは 1 行 6 列でなく、2 行 3 列にしています。

実際の例

• 秘密情報
  

• シェア画像

1 つ目	2 つ目	3 つ目	4 つ目

• 2 つのシェアから再構成した秘密情報 (正しく再構成できない場合)

$1 \vee 2$	$1 \vee 3$	$1 \vee 4$	$2 \vee 3$	$2 \vee 4$	$3 \vee 4$

• 3 つのシェアから再構成した秘密情報

$1 \vee 2 \vee 3$	$1 \vee 2 \vee 4$	$1 \vee 3 \vee 4$	$2 \vee 3 \vee 4$

• 4 つのシェアから再構成した秘密情報

おわりに

この記事では $(2, 2)$ と $(3, 4)$ の構成法を紹介しました。
一般化した $(k, n)$ 視覚復号型秘密分散法の構成もシステマティックに行うことができますが、説明が長くなってしまうため、入門として特殊化した 2 種類の説明をしています。
また、再構成した画像は、横へと伸びたものになっていましたが、縦横比を保つような構成も可能です。
初めは $(2, 2)$ の場合にうまく構成する方法を考えてみると良いと思います。
次の記事では、今回説明したもののプログラムによる実装をしたいと思います。