再考、NanoDet plusの post-processing

0.Prologue

不満!!
先般投稿した"NanoDet plus"記事の post-processingがエレガントでない。decode_boxes/2が、なんともごちゃごちゃしていて、小生のレベルの低さを如実に物語っているようで……気に食わない。Boxのデコードの理解を優先したと言ういい訳はこの際却下。

と言う訳で、素人なりに decode_boxes/2を再考・再構築してみようと思う。
恥ずかしながら元のコードは下記の如くだった。

  def decode_boxes(tensor, world \\ {}) do
    max_index = Nx.axis_size(tensor, 0) - 1

    for(i <- 0..max_index, do: decode_box(tensor[i], world))
    |> Nx.stack()
  end

  def decode_box(tensor, world \\ {}) do
    grid_x = Nx.to_number(tensor[-3])
    grid_y = Nx.to_number(tensor[-2])
    arm    = Nx.iota({8}) |> Nx.multiply(tensor[-1])  # [0, pitch, 2*pitch, ... 7*pitch]

    # private func: decode probability table to wing.
    wing = fn t ->
      max = Nx.reduce_max(t)

      {weight, sum} =
        Nx.subtract(t, max)  # prevent exp from becoming too big
        |> Nx.exp()
        |> (&{&1, Nx.sum(&1)}).()

      # mean of probability list
      Nx.dot(weight, arm) |> Nx.divide(sum) |> Nx.to_number()
    end

    {scale_w, scale_h} = scale(world)

    [
      scale_w * (grid_x - wing.(tensor[0..7])),
      scale_h * (grid_y - wing.(tensor[8..15])),
      scale_w * (grid_x + wing.(tensor[16..23])),
      scale_h * (grid_y + wing.(tensor[24..31]))
    ]
    |> keep_within(world)  # keep coners of the box within the original photo.
    |> Nx.stack()
  end

1.Design Policy

"NanoDet plus"の推論結果は実質的には表なのだが tensorとして出力される。となると、Elixirだと Nxだけで推論結果を加工するのが王道であろう。なにせ、Nxには Numpy同様に tensor演算をコンパクトに表現できる関数が数々と用意されているのだから[*1]。ふむ、これを巧みに利用するのがエレガントかつ玄人っぽく見えるに違いない。左様、あくまでも見た目勝負で、処理速度など眼中にないである

さて、decode_boxes/2の心臓部は先の記事でも触れた通り「疑似確率分布」の平均(重心)を求める部分だ。そこでは、ベクトル同士の内積(Nx.dot/2)やベクトル要素の総和(Nx.sum/1)を計算していた。それもご丁寧に、候補Box一つ一つに対してちまちまと……不細工 orz。ここが再考のポイントだろう。さあ、どうするかな?

Nx.dot/2は引数にmatrix(tensor rank=2)とvector(tensor rank=1)を取ることができ、第一引数にmatrix、第二引数にvectorを与えると下記の結果を返してくるようだ。つまり、matrixの行vector各々とvectorの内積が一挙に計算できるのだ。もしも行vectorが候補Box各々の「疑似確率分布」だとすれば……これは使える

Nx.dot\Biggl(
\Biggl(\begin{matrix}
a&b&c\\
d&e&f\\
g&h&i
\end{matrix}\Biggr),
(x,y,z)
\Biggr)
=
\Biggl(\begin{matrix}
a*x+b*y+c*z\\
d*x+e*y+f*z\\
g*x+h*y+i*z
\end{matrix}\Biggr)

一方、Nx.sum/2も引数にmatrixを与えることができ、その際に総和を求める軸を同時に指定すれば、下記の結果を得ることができる。つまり、こちらもmatrixの行vector各々の総和を一挙に計算できるのだ。しめしめ

Nx.sum\Biggl(
\Biggl(\begin{matrix}
a&b&c\\
d&e&f\\
g&h&i
\end{matrix}\Biggr),
axes: [1]
\Biggr)
=
\Biggl(\begin{matrix}
a+b+c\\
d+e+f\\
g+h+i
\end{matrix}\Biggr)

次章では、これら二つのテクニックを中心に Nxを巧みに利用して decode_boxes/2の再構築に挑戦する。

尚、tensorの slicingや transpose、concatenate等は必要最小の使用に抑えることにする。できるだけ tensorの複製(重い処理?)を避けたいが故だが、これらの実装を詳しく調べた訳ではないので真相は定かではない。まぁ、触らぬ神に祟り無しってことだ。

[*1]偉そうに書いているが、小生は Nxも Numpyもド素人である

2.Redesigning

decode_boxes/2の再構築は、"NanoDet plus"とは別のnotebookで進めることにする。単体で動作確認ができる様に、予め "NanoDet plus"のnotebookで decode_boxes/2の入力tensorと出力tensorをファイルに落としておく。

  ...
  File.write!("ex_check/boxes.bin", Nx.serialize(boxes))
  Npy.savecsv(boxes, "ex_check/boxes0.csv")

  boxes = decode_boxes(boxes, {width, height})

  Npy.savecsv(boxes, "ex_check/boxes1.csv")
  ...

ここで、簡単に入力tensor、出力tensorの仕様を確認しておこう。

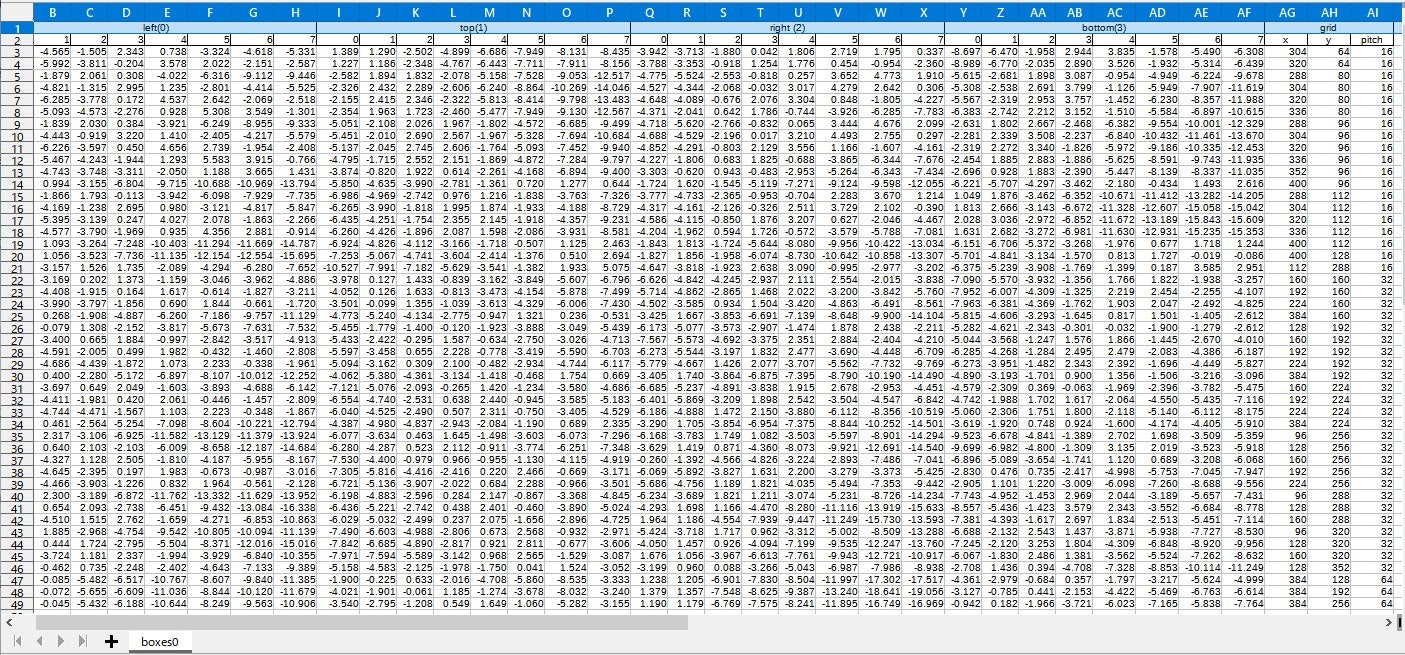
入力tensorは下の様な表(tensor rank=2)で、各行はそれぞれ候補Boxを表している。一方、列は左から順に Boxの左端推定の疑似確率分布(8列)、同上端推定(8列)、右端推定(8列)、下端推定(8列)、そしてBoxが属するグリッドの座標(x,y)、大きさpitchが続いている。左・上・右・下の疑似確率分布は、"NanoDet plus"モデルの出力値そのものである。また tensorの軸は、行方向(紙面垂直方向)が 0軸、列方向(紙面水平方向)が 1軸となる。

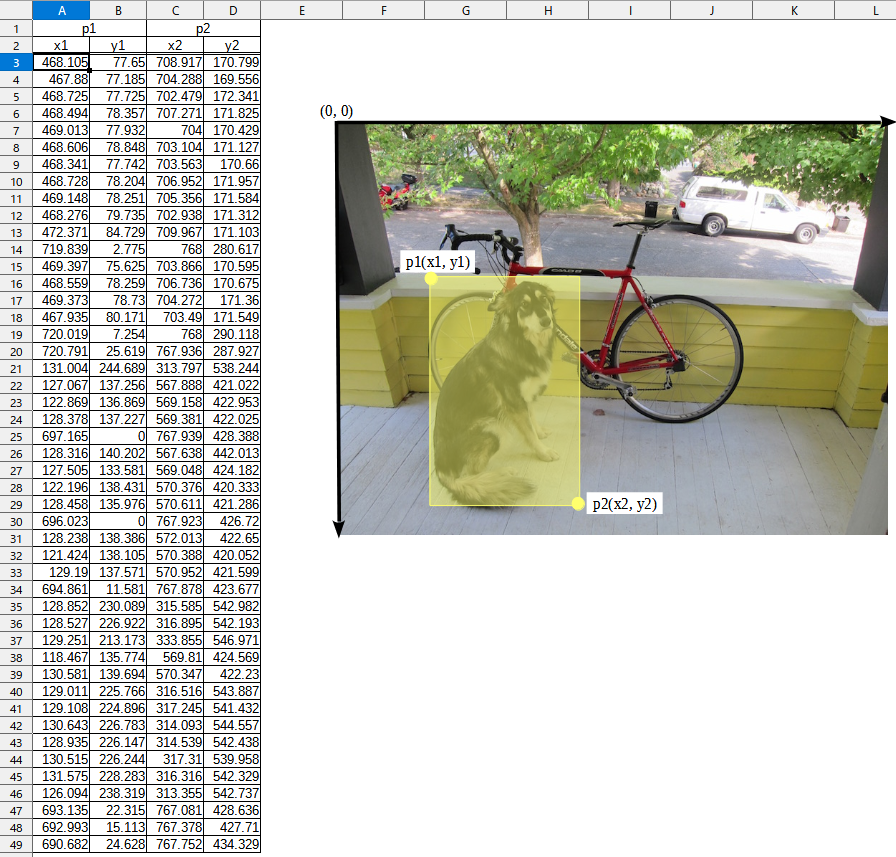
この入力に対する出力tensorは下の通りで、入力画像の座標系における各候補Box(行)の左端(x1)、上端(y1)、右端(x2)、下端(y2)の座標値が列方向に順に並んだ表となっている。つまり、候補Boxの左上頂点p1と右下頂点p2の座標が並んでいるのだ。

では、decode_boxes/2の再構築に取り掛かろう。
上で見たように、入力tensorには複数の属性が含まれている。このままでは decode_boxesの計算が出来ないので、tensorの1軸でslicingして 左,上,右,下の疑似確率分布とグリッドの座標,大きさを取り出そう。

# tensorから左(0),上(1),右(2),下(3)の疑似確率分布(8列)を取り出す
Enum.map(0..3, fn i ->
  Nx.slice_along_axis(tensor, 8*i, 8, axis: 1)
  ...
end)

# tensorからグリッドの座標,大きさを取り出す
[grid_x, grid_y, pitch] = Enum.map(32..34, fn i ->
  Nx.slice_along_axis(tensor, i, 1, axis: 1) |> Nx.squeeze()
end)

さらに、次の式に基づいて疑似確率分布からwingを求める。ここで、一章で再考した Nx.dot/2, Nx.sum/2のテクニックを用いる。バンッと一挙に全候補Boxのwingを計算するのだ

格子点からBBOX端までの距離 wing = pitch*\frac{\sum_{i}(i*e^{dist[i]})}{\sum_{i} e^{dist[i]}}

# tensorから左(0),上(1),右(2),下(3)の疑似確率分布(8列)を取り出す
Enum.map(0..3, fn i ->
  # 疑似確率分布の重心wingを求める
  exp  = Nx.slice_along_axis(tensor, 8*i, 8, axis: 1) |> Nx.exp()
  wing = Nx.dot(exp, Nx.iota({8})) |> Nx.divide(Nx.sum(exp, axes: [1])) |> Nx.multiply(pitch)
  ...
end)

最後に、グリッド座標にwingを足し/引きして Box端の座標を求め、それを入力画像に合うようにスケーリングする。……なのだが、これらの処理は左(0),上(1),右(2),下(3)で異なるものになる。case分岐するしか手はないか

# tensorから左(0),上(1),右(2),下(3)の疑似確率分布(8列)を取り出す
Enum.map(0..3, fn i ->
  # 疑似確率分布の重心wingを求める
  exp  = Nx.slice_along_axis(tensor, 8*i, 8, axis: 1) |> Nx.exp()
  wing = Nx.dot(exp, Nx.iota({8})) |> Nx.divide(Nx.sum(exp, axes: [1])) |> Nx.multiply(pitch)

  # 左(0),上(1),右(2),下(3)のそれぞれのBox端を求め、入力画像に合うようにスケーリングする(scale_*)
  case i do
    0 -> Nx.subtract(grid_x, wing) |> Nx.multiply(scale_w) |> Nx.max(0.0)
    1 -> Nx.subtract(grid_y, wing) |> Nx.multiply(scale_h) |> Nx.max(0.0)
    2 -> Nx.add(grid_x, wing) |> Nx.multiply(scale_w) |> Nx.min(img_w)
    3 -> Nx.add(grid_y, wing) |> Nx.multiply(scale_h) |> Nx.min(img_h)
  end
  ...
end)

以上を整理してまとめると、新decode_boxes/2は下の様になる。
まあまあスッキリしたかな?

defmodule PostNanoDet do
  @shape {416, 416}
  @arm   Nx.iota({8})

  def decode_boxes(tensor, {img_w, img_h} \\ {}) do
    [grid_x, grid_y, pitch] = Enum.map(32..34, fn i ->
      Nx.slice_along_axis(tensor, i, 1, axis: 1) |> Nx.squeeze()
    end)

    scale_w = img_w / elem(@shape, 0)
    scale_h = img_h / elem(@shape, 1)

    Enum.map(0..3, fn i ->
      exp  = Nx.slice_along_axis(tensor, 8*i, 8, axis: 1) |> Nx.exp()
      wing = Nx.dot(exp, @arm) |> Nx.divide(Nx.sum(exp, axes: [1])) |> Nx.multiply(pitch)

      case i do
        0 -> Nx.subtract(grid_x, wing) |> Nx.multiply(scale_w) |> Nx.max(0.0)
        1 -> Nx.subtract(grid_y, wing) |> Nx.multiply(scale_h) |> Nx.max(0.0)
        2 -> Nx.add(grid_x, wing) |> Nx.multiply(scale_w) |> Nx.min(img_w)
        3 -> Nx.add(grid_y, wing) |> Nx.multiply(scale_h) |> Nx.min(img_h)
      end
      |> Nx.reshape({:auto, 1})
    end)
    |> Nx.concatenate(axis: 1)
  end
end

それでは、ファイルに保存しておいた入力tensorを新decode_boxes/2に与えて動作を確認してみよう……良さそうな雰囲気だ。

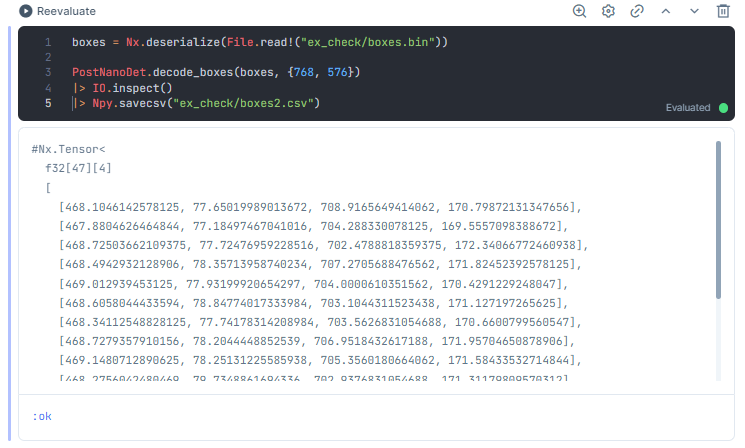
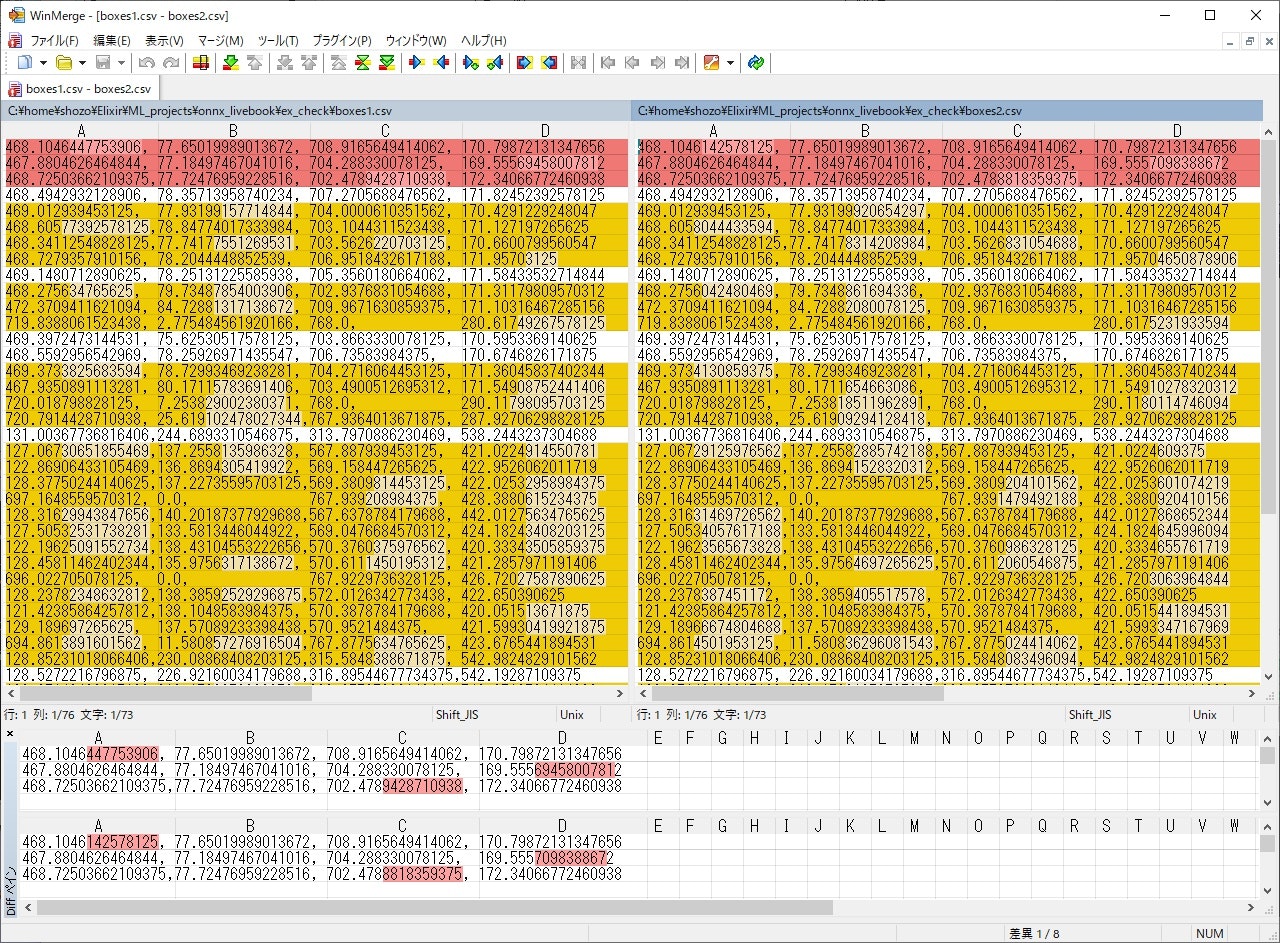
より詳しくチェックするために、新/旧decode_boxes/2に同じ入力を与えたときの出力tensorを比較してみよう……小数点第4～5位辺りで差異があるようだ。有効桁数は大体 6～7桁かな。

tensorのデータ型は float32なので仮数部は (23+1)ビット。10進数に直すとその有効桁数は、

log(2^{24}) \fallingdotseq 7.2247198959

ほぼ7桁と言えそう。ということは、先の差異は float32演算による丸め誤差と見做しても良さそうかな

ということで、decode_boxes/2の再構築完了だ

3.Epilogue

どうだろう、ちょっとはエレガントになっただろうか?
もしも入力tensorが転置されていれば、また別の道があったかも知れない。

「この手のリファクタリングは多分にヒューリスティックだなぁ」と思う一件であった。