Pythonによる数値計算-1次元電子系のパイエルス転移

#はじめに
　今回は数値計算の手法にこだわらずPythonにおけるmatplotlibの簡単な使い方について書きたいと思います。数値計算とは直接的な関係はないですが可視化という意味では重要ですし、本投稿を読んでいただいた方の中にプログラミングは初心者だけど綺麗なグラフくらいは描けるようになりたいと考えている方がいれば十分に役立てるはずです。
　題材としては1次元電子系におけるパイエルス転移です。難しそうに見えるかもしれませんが、数値計算としてはただ数式をグラフにするだけなので細かい説明を読み飛ばしてmatplotlibの使い方の部分まで飛んでいただければ大丈夫です。

#1次元電子系のパイエルス転移
####・分極関数　
　金属電子に波数Q、角振動数$\omega$の弱い摂動を加えると、物質中の金属電子の密度は結晶格子と同じ周期で空間的に変化する。電子密度の空間変化、つまり振幅の大きさは格子の周期ポテンシャルが弱い場合には小さい。これはアルカリ金属などの自由電子モデルが成り立つような系に対応する。一方、強束縛電子モデルが成り立つような分子性物質や酸化物導体、半導体シリコンなどでは、自由電子モデルが成り立つような系に比べて相対的に振幅が大きくなる。
　波数Qで空間的に振動するポテンシャル$V_{Q}$を外部から加えると、これに応じて電子系は同じ波数の密度変調$\rho_{Q}$を生じるはずで、ポテンシャルが十分小さければ密度変調はポテンシャルに比例する。

\rho_{Q} = - \chi(Q)V_{Q}

ここで$\chi(Q)$は分極関数と呼ばれる比例係数である。

####・ネスティング
　自由電子のハミルトニアンは$H_{0}={p^{2}}/{2m}$であり、波数kの固有状態の波動関数は

\phi_{k}=\frac{1}{\sqrt{V}}\exp\left(ikr+i\frac{E_{k}t}{\hbar}\right)

ここで$E_{k}=\hbar^{2}k^{2}/2m$であり、Vはは系の体積である。摂動として

V(r,t)=V_{Q}\exp(iQr+i\omega t+\alpha t)

を加える。$\alpha$は無限の過去からゆっくりと摂動を加えるためのものである。全ハミルトニアンの固有状態における波動関数$\psi_{k}$は

\psi_{k}=\phi_{k}+a_{k+Q}\phi_{k+Q}

展開係数$a_{k+Q}$が1に比べて十分小さい。

a_{k+Q}(t)=\frac{V_{Q}\exp(i\omega+\alpha t)}{E_{k}-E_{k+Q}+\hbar\omega-i\hbar\alpha}

また、電子密度は

\rho(r)=\sum_{k}{|\psi_{k}|^2}

で与えられる。これに波動関数$\psi_{k}$を代入し、空間的に一様な平均密度を表す項を落とした残りが電子密度の空間変調を与える。電子密度を$\delta\rho(r)=\rho_{Q}\exp(iQr)$のように表すと分極関数の定義より

\chi(Q)=\frac{1}{V}\sum_{k}{\frac{f_{k+Q}-f_{k}}{E_{k}-E_{k+Q}}} \tag{1}

簡単のために$T=0$とすると分極関数がゼロにならないためには$E_{k}$と$E_{k+Q}$がフェルミエネルギーを挟まなければならない。1次元系では

\chi(Q)=\frac{2m}{\pi \hbar^2 Q}\ln \left|\frac{Q+2k_{F}}{Q-2k_{F}} \right| \tag{2}

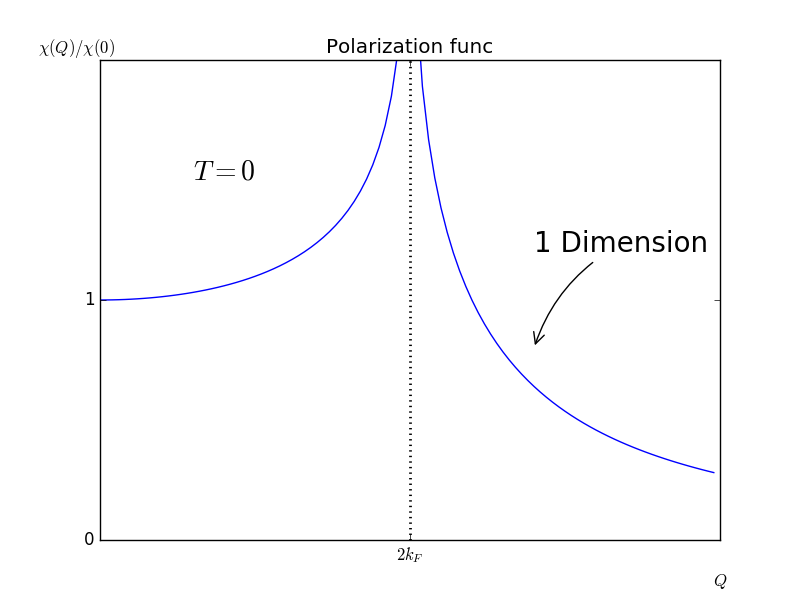
となる。よって1次元電子系の分極関数は振動数が$2k_{F}$のときに発散する。この特異性は2次元や3次元では緩やかになる。次元によって変わる分極関数の振る舞いの違いはフェルミエネルギーの性質によるものである。フェルミエネルギーは摂動による波数の平行移動$k\rightarrow k+Q$に伴って移動する。1次元の場合は波数の平行移動に対してフェルミ面がすべて一致する。しかし、2次元(等方的)になるとフェルミ円筒は平行移動に対しては線でのみ一致する。つまり、次元性が上がるにつれて波数の平行移動に対して同じエネルギーを持つkが少なくなる。すると式(1)の分母を発散させるようなkが少なくなる。したがって分極関数の性質は系のフェルミ面の形状によって変わり、波数を平行移動した先のフェルミ面と元のフェルミ面との重なり具合が大きいほど分極関数を増大させる。このようなフェルミ面の重なりをネスティングという。
####・1次元電子系のパイエルス転移
　1次元格子-電子系において格子が歪むことで1次元電子系は周期的な摂動を受ける。これによって前述したように電子系は密度波を生じる。電子系は密度波を生じることでエネルギーを下げるが、格子系は歪みによってエネルギーが増加する。そのため、電子系のエネルギーの減少分が格子の歪みによるエネルギーの増加分をしのげば格子歪みと電視密度の波が生じることになる。1次元電子系では$Q=2k_{F}$の振動数を持つ格子歪みによって生じる。この二つの波の振動数が$Q=2k_{F}$になるとき、ちょうど格子歪みの一周期の中に二つの電子が入ることになる。Pauliの排他律によって電子は隣の格子へ移動することができなくなる。したがって系は金属状態から絶縁体へ変化する。これをパイエルス転移という。

#数式の可視化
　前置きが長くなりましたが以降では式(2)をグラフに描きたいと思います。

\chi(Q)=\frac{2m}{\pi \hbar^2 Q}\ln \left|\frac{Q+2k_{F}}{Q-2k_{F}} \right| 

次のプログラムを実行してみてください。

plot.py

import math, pylab


#--------数値計算--------#
step = 100
x = [0.00]*step
y = [0.00]*step

for i in range(step):
    x[i] = i*2/step
    if x[i] == 1.0:         #x[i]が1.0のとき発散を避ける
        x[i] = 1.0000001

#x[i]が0.0のとき発散を避ける
x[0] = 0.00001



for i in range(step):
    y[i] = (math.log(abs((x[i]+1)/(x[i]-1)))/x[i])/(math.log(abs((x[0]+1)/(x[0]-1)))/x[0])

#------------------------#



#グラフを描く
pylab.plot(x,y)

#グラフのタイトル
pylab.title('Polarization func')

#x軸のラベル、Texが使えて、表示する位置も決められる
pylab.xlabel('$Q$', x = 1)

#y軸のラベル、rotationを定義することで文字の向きを決められる
pylab.ylabel('$\chi(Q)/\chi(0)$', rotation = 0, y = 1)

#y軸の最大値と最小値を設定する
pylab.ylim(ymin = 0, ymax = 2)

pylab.axvline(1,ls = ':' , c = 'black', lw = 2)


#x軸の値を設定する
#Texを使った文字も表示できる
#1.0のデータ点をフェルミ波数の2倍に書き換える
pylab.xticks([1.0], ["$2k_{F}$"])

#y軸の値を設定する
#表示する数値を0と1のみにする
pylab.yticks([0,1])

#text関数で注釈を加える
pylab.text(0.3,1.5, '$T = 0$', family = 'monospace', fontsize = 20, color = 'black')

#annotate関数で注釈を加える
pylab.annotate(
    '1 Dimension',                          #注釈の内容
    xy = (1.4,0.8),                           #arrowpropsの矢印の終点
    xytext = (1.4, 1.2),                      #注釈コメントの位置。arrowprops矢印の始点
    arrowprops = dict(arrowstyle = "->",        #矢印の設定
                    connectionstyle = "arc3,rad=.2",
                    facecolor = 'black'),
    fontsize = 20,
)
pylab.show()

　プログラムを実行すると下のようなグラフが出来上がるはずです。パラメータの説明はプログラム内に書いておいたので、パラメータをいじってみてください。関数はプログラム内にあるもの以外にもたくさんあるのでチュートリアルや他の方々が書かれたプログラムを読んで試してみるといいでしょう。