Pythonによる数値計算-放物運動(Euler法)

はじめに

　前回は放射性物質の半減期をテーマとして扱いました。今回のテーマは重力加速度のもとで運動する物体の放物運動です。前回と同じ手法を使って別の問題を扱うことにしました。放物運動は高校物理でも出てくる基本的で重要な内容です。あらかじめ作ろうとしているプログラムを宣言しておきましょう。今回作ろうとしているのは横軸および縦軸が位置を表すグラフです。ある角度で射出された物体がどのような軌道を描くのかをみてみましょう。
　　重力加速度のもとで物体は、Newtonの運動方程式に則って運動することがわかっています。Newtonの運動方程式は次のように表されます。

m\alpha = F  \tag{1}

ここでmは物体の質量、$\alpha$は物体の加速度、そしてFは物体に加わる力を意味します。Pythonによる数値計算入門-Part1でも述べたように、まず準備するべきは数値計算の手法で解くことのできる数式を用意することですが、この数式を数値計算の手法で解くのは少し厄介です。
　そこで今まで後回しにしてきた数式の変形を行いましょう。式(1)は書き換えると次のようにかけることがわかります。

\frac{dv}{dt} = F \tag{2}

加速度が速度の微分であることを用いました。また簡単のために式を単位質量あたりになるようにしました。質量を考える場合はパラメータとして含めれば良いだけなので運動の本質には影響しません。
　さて、これで数値計算の手法で解くことができるかと言われれば、まだ複雑です。一つは物理でよくやるベクトル分解です。この場合は物体にかかる力が重力ですので、重力のかかる方向をyとしてそれに垂直に交わるようにx軸をとったxy平面を考えるのが良いでしょう。そこで式(2)を次のようにベクトル分解します。

\frac{dv_{x}}{dt} = 0 \tag{3}

\frac{dv_{y}}{dt} = -g \tag{4}

式(3)はx軸方向の運動方程式です。力がかかっていないので右辺は0になります。一方、式(4)は重力加速度が-y方向にかかっていますから右辺は-gになります。式(3)と(4)から求めることができるのは速度の時間変化ですので、次の式も加えることで物体の軌道を計算できるようにしましょう。

\frac{dx}{dt} = v_{x} \tag{5}

\frac{dy}{dt} = v_{y} \tag{6}

　これで数式を数値計算の手法で解くことのできる状態まで持ってくることができました。次に行うのはパラメータの設定です。定義域の設定と運動の初期値の設定が必要になります。定義域に関しては、求めたい軌道がグラフの中に入っていれば良いので難しくはありません。運動の初期値の設定とは、この場合は初速度、重力加速度、射出角度を意味しています。式(3)および(4)を完全に解くためにはこれらのパラメータを定義しなければなりません。これらはプログラムを説明する際にまとめて説明することにします。

#Euler法
前稿のEuler法をそのまま適用してみましょう。自分の力で式(3)から(6)までを変形できるようになりましょう。答えは次のように表されます。

v_{x,i+1} = v_{x,i}\tag{7}

v_{y,i+1} = v_{y,i}-g\Delta t \tag{8}

x_{i+1} = x_{i}+v_{x,i}\Delta t \tag{9}

y_{i+1} = y_{i}+v_{y,i}\Delta t \tag{10}

前回も説明したように$\Delta t$が十分小さければ$O({\Delta t}^{2})$の項は無視できます。そのことが理解できていればEuler法が上式のように書けることも理解できるでしょう。

#計算
では全体のプログラムをみてみましょう。

parabola.py

import math, pylab

#①
g = 9.8
v0 = 30
angle = 45.0
dt = 0.01

#②
x = [0.0]
y = [0.0]
vx = [v0*math.cos(angle*math.pi/180.0)]
vy = [v0*math.sin(angle*math.pi/180.0)]

#③
i = 0
while y[i] >= 0:

    x += [0.0]
    y += [0.0]
    vx += [0.0]
    vy += [0.0]

    x[i+1] = x[i]+vx[i]*dt
    y[i+1] = y[i]+vy[i]*dt
    vx[i+1] = vx[i]
    vy[i+1] = vy[i]-g*dt

    i = i+1

pylab.plot(x,y)
pylab.ylim(ymin = 0)
pylab.show()

①:まずは初期値の設定です。重力加速度はご存知の通り9.8$[m/s^{2}]$です。初速度は適当に30$[m/s]$にしておきました。射出角度は45°で、分割数は0.01[s]ごとにしました。
②:各分割点に対応した計算値を出すために初期値を代入しておきます。前々回までとの違いは最初にリストの初期値を全て決めてしまわないことです。各リストへの値の格納は次のwhile文で行います。
③:yが正である間計算を繰り返します。while文の中はEuler法であることを確認してください。
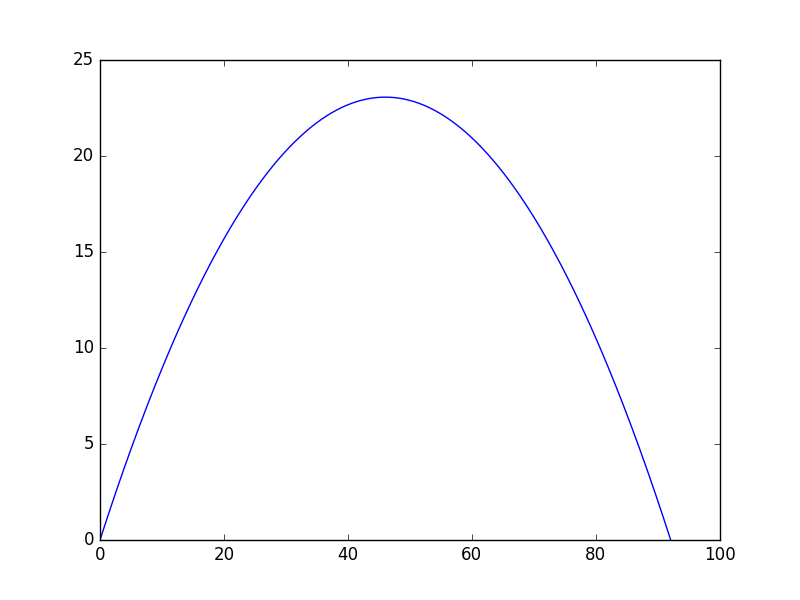
　このプログラムを実行してみてください。放物線が出力されることがわかると思います。以上で目的の結果が得られました。

#最後に
　物理的に興味があるのは例えば空気抵抗がある場合です。wikipediaなどを参考に空気抵抗のある場合の運動方程式を数値計算で解いてみましょう。また、パラメータの設定を色々と変えてみてください。角度以外のパラメータが同じ場合、角度が45°のときがもっとも遠くまで放物線が伸びていることも確認できます。