初めに
(Quasi-)Monte Carlo法について,理論的な話は良く分かっていないのだが,実験から傾向を観察する.理論的な議論は,鈴木&合田2020が詳しい.
(Quasi-)Monte Carlo法
乱数を用いて計算をする方法である.乱数なので,ランダムネスが含まれるので,(ほぼ)正しい計算結果になることもあれば,正しくない結果になることもある.
区別として,
- 疑似乱数で以て計算する方法はMonte Carlo法(MC)
- 準乱数で以て計算する方法はQuasi-Monte Carlo法(QMC)
と呼ばれる.
標本サイズ$N$と近似誤差$\varepsilon$の関係を記す:
- MC: $\varepsilon \sim \mathcal{O} \left[ 1 / \sqrt{N} \right]$
- QMC: $\varepsilon \sim \mathcal{O} \left[ (\log N)^d / N \right]$
ほどの速度で収束する($d$は空間次元).QMCについては,振る舞いの良い関数では$\varepsilon \sim \mathcal{O} \left[ 1 / N \right]$程度で収束するらしい(何を以て振る舞いが良いと言うのか知らないのだが,,).
2024/01/09追記
この良い性質のことを「有界変動」というらしい.まだ全く分かっていないが,名前だけメモしておく.
Experiment
先に記した通り,(ほぼ)正しい計算結果になることもあれば,正しくない結果になることもある.したがって,同じ実験を256回繰り返し,その平均値を観察する.
分布の観察
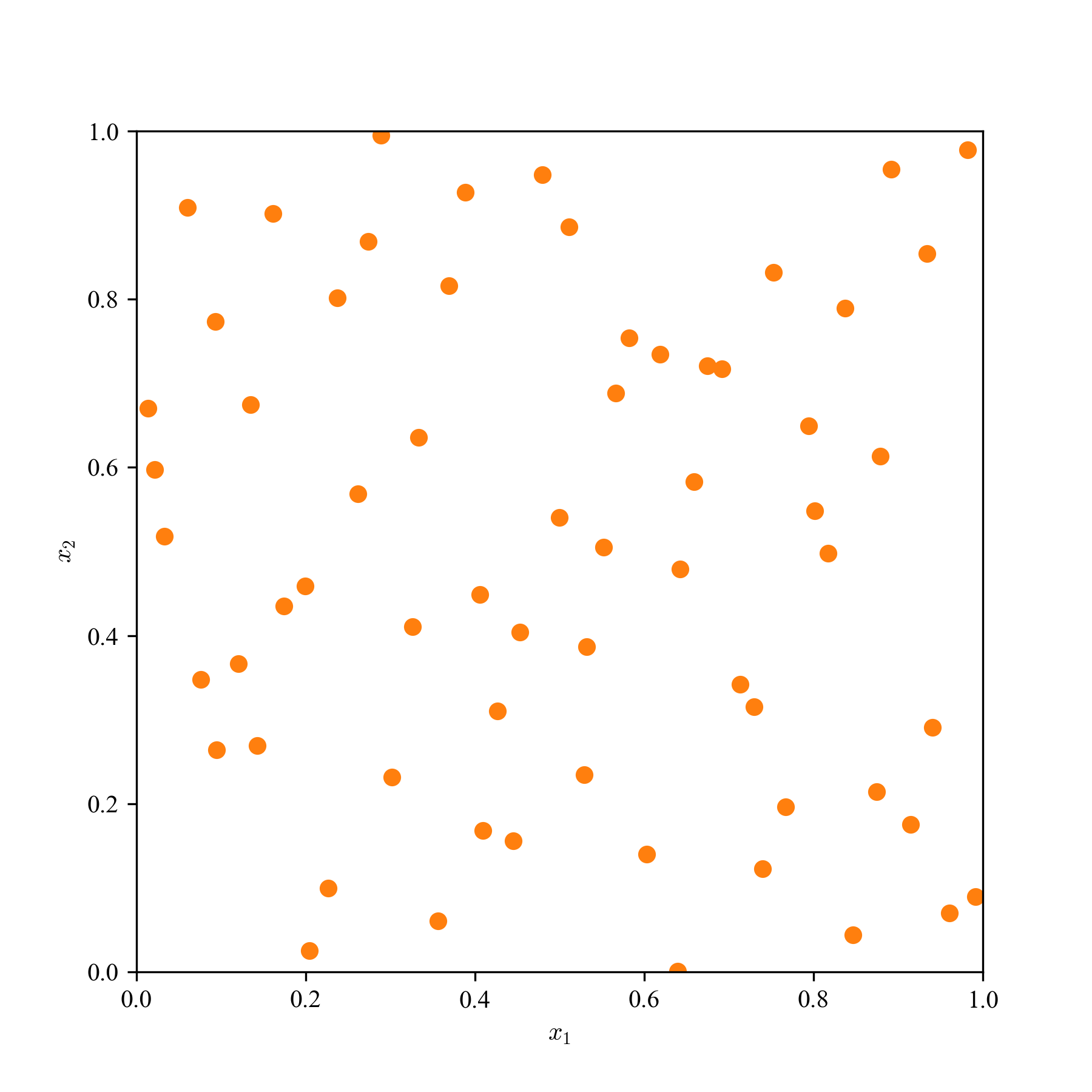
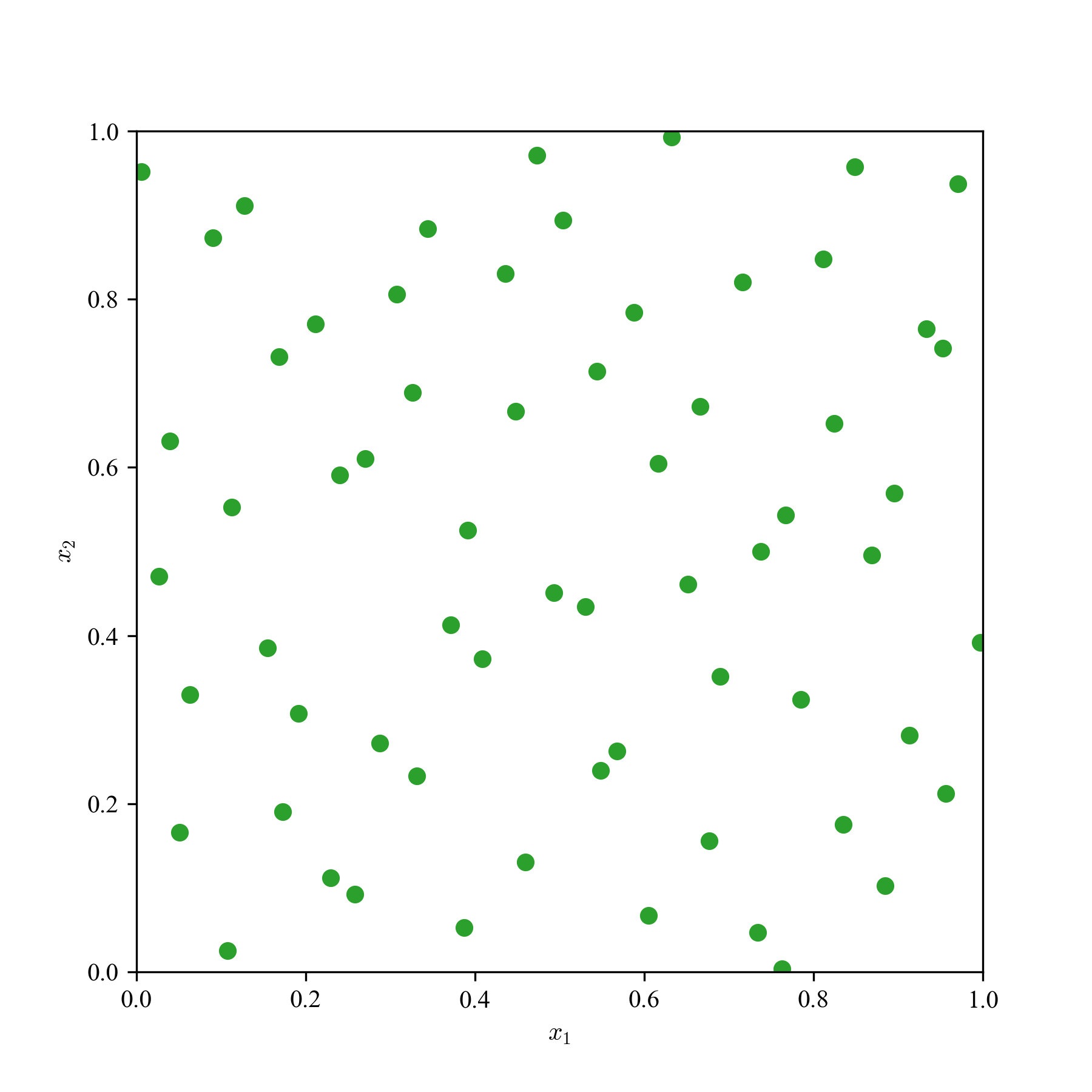
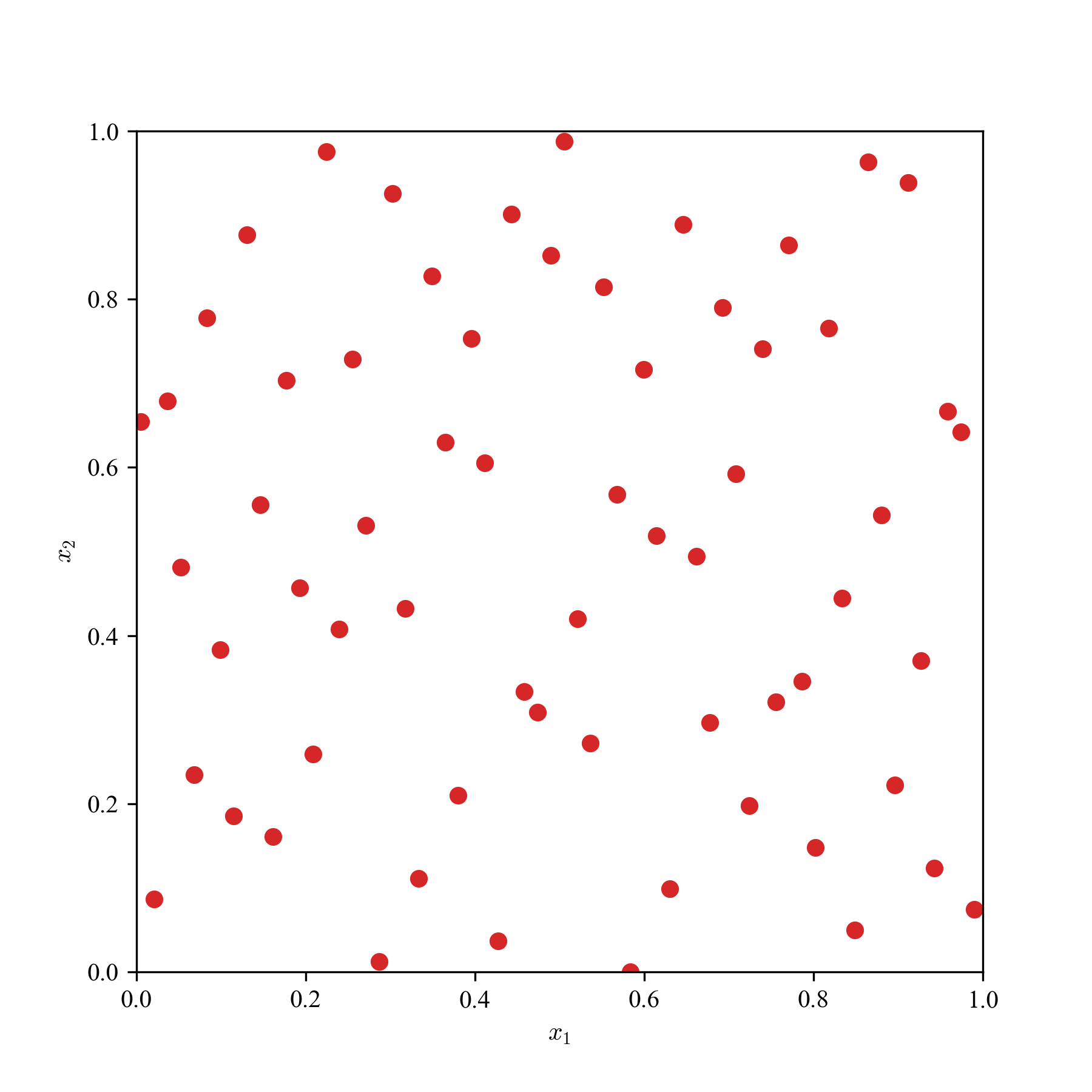
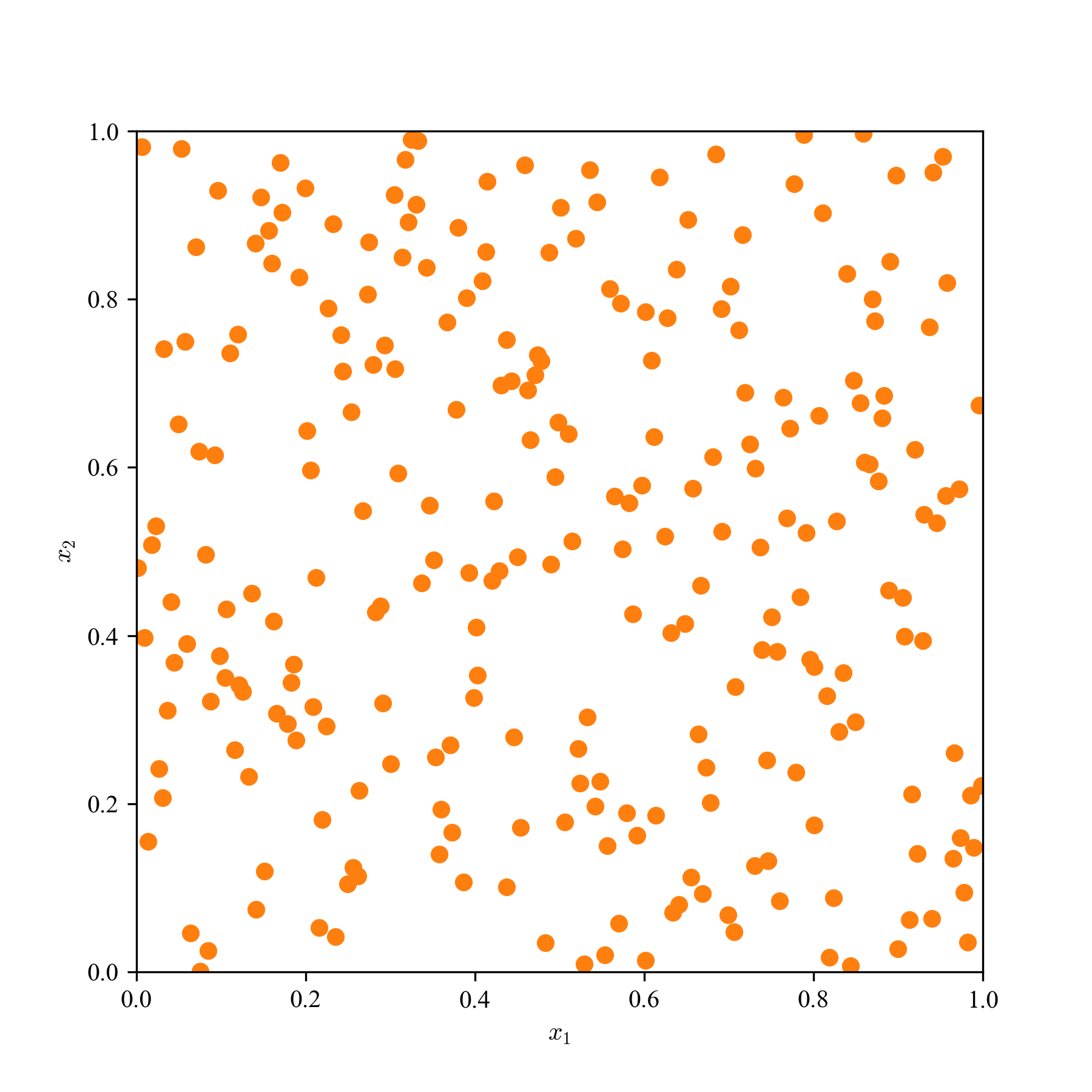
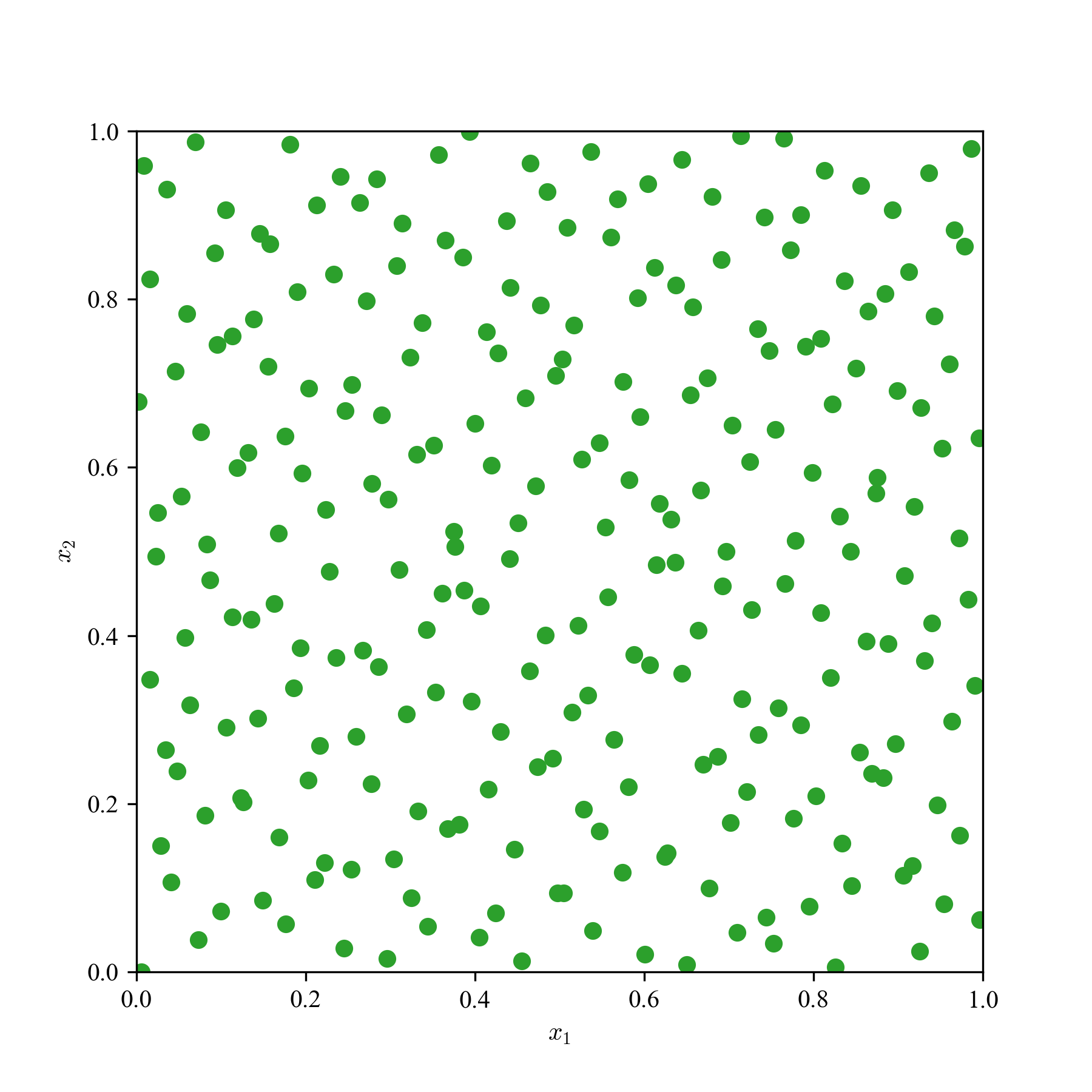
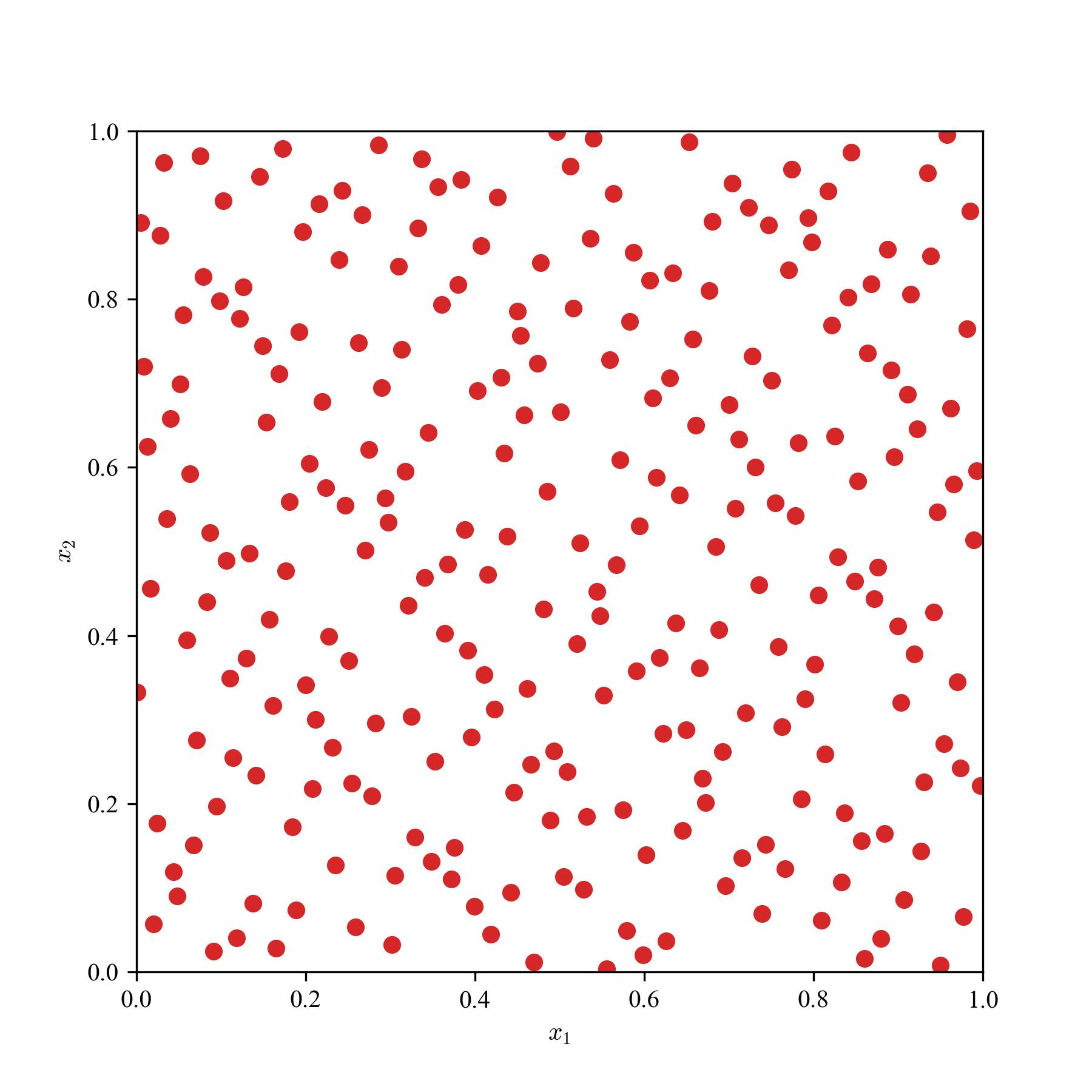
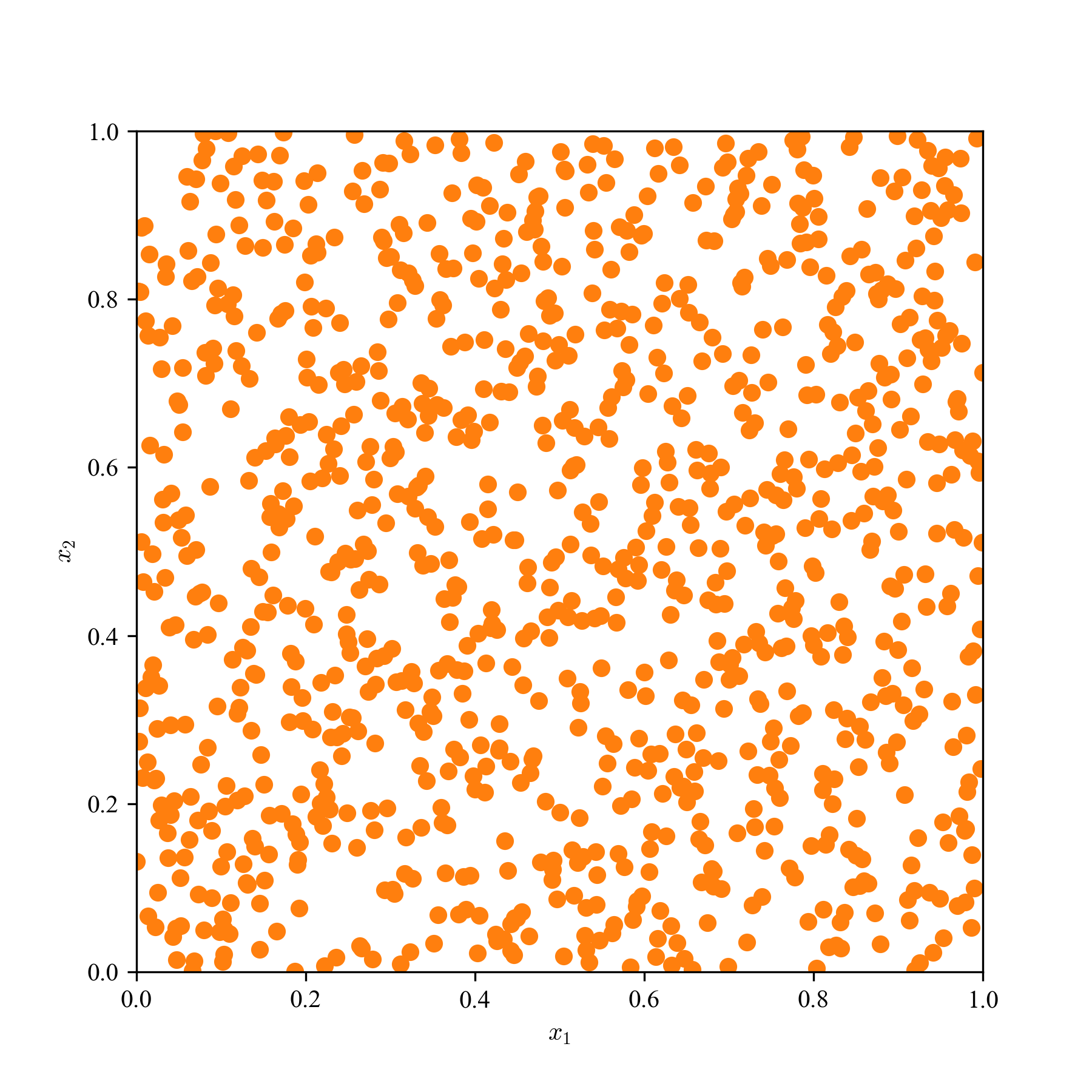
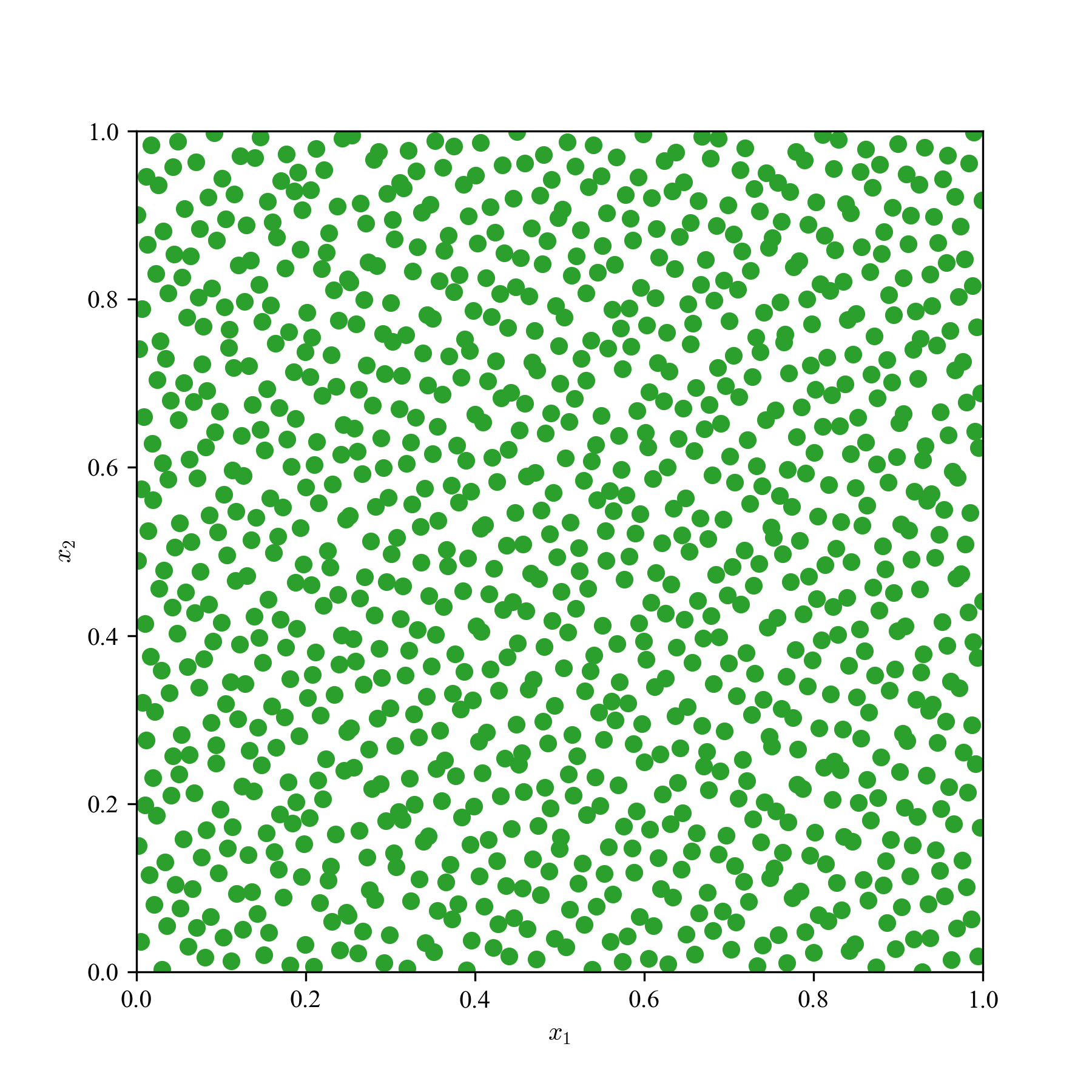
一様乱数(MC)とQMCの求積点を2次元空間に散撒き,見た目の違いを観察する.
a: 64点,b: 256点,c: 1024点の3パターンで,単なる一様乱数,LHS,Sobol'列,Halton列の結果を貼り付ける.
| MC | LHS | Sobol' | Halton | |
|---|---|---|---|---|
| a | 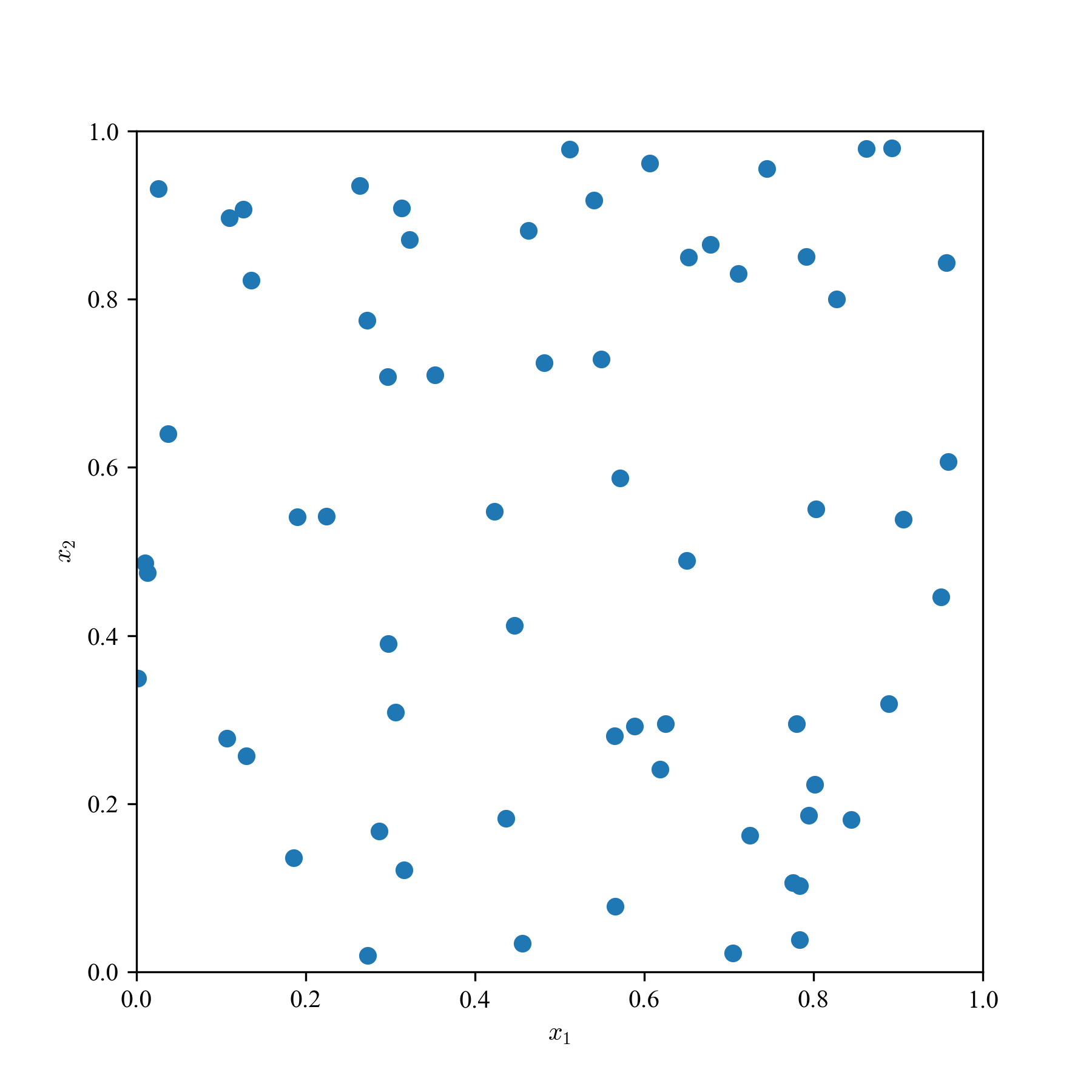 |
 |
 |
 |
| b | 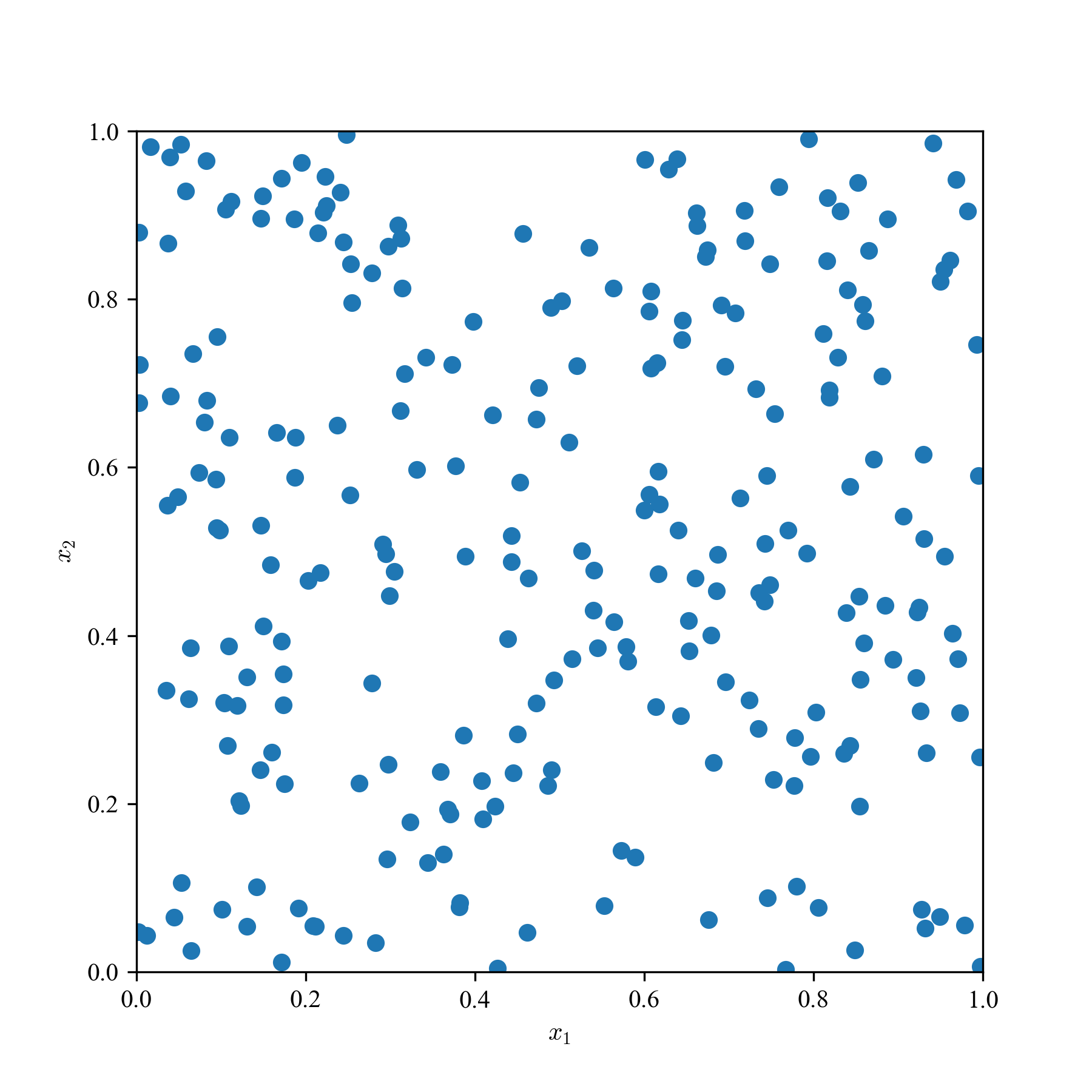 |
 |
 |
 |
| c | 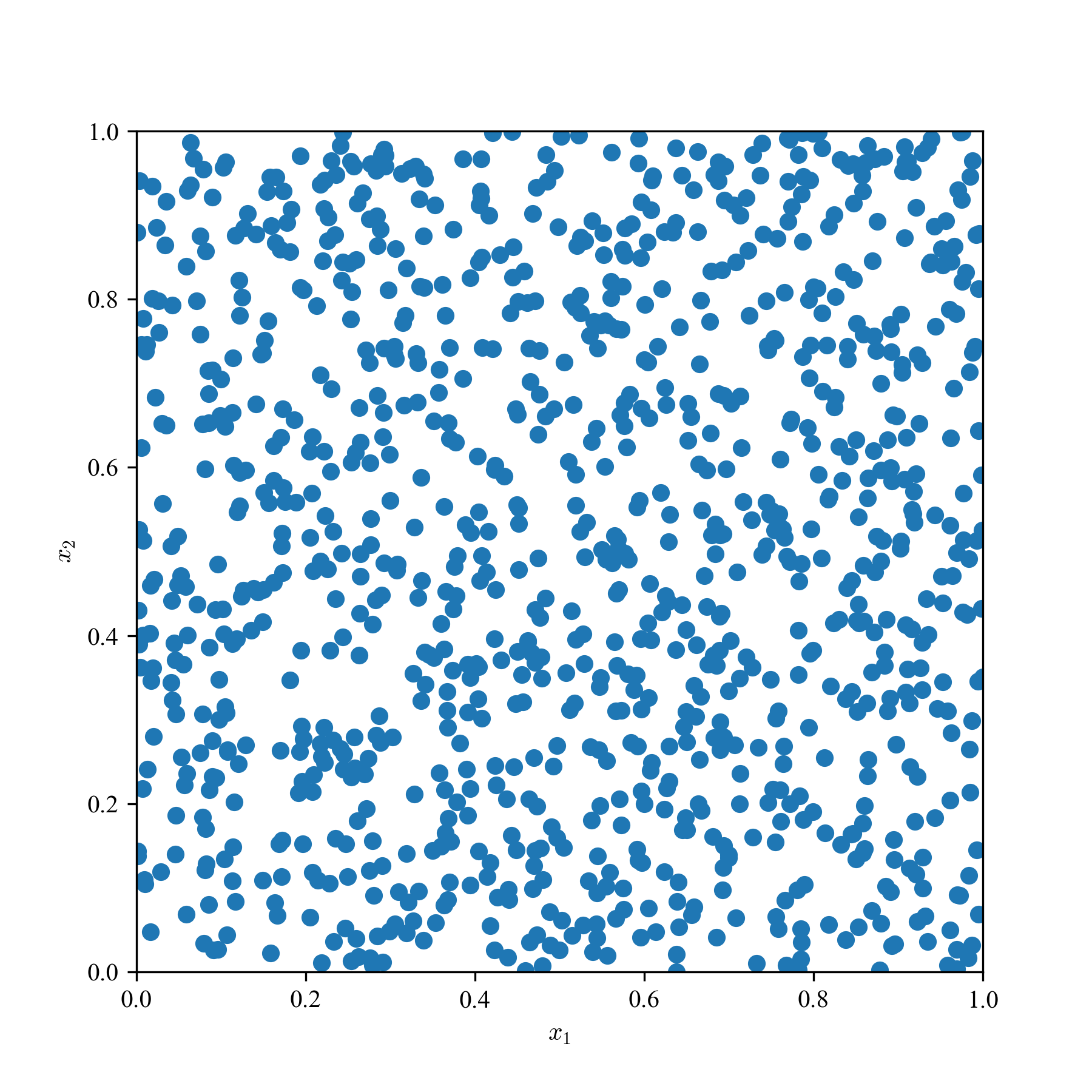 |
 |
 |
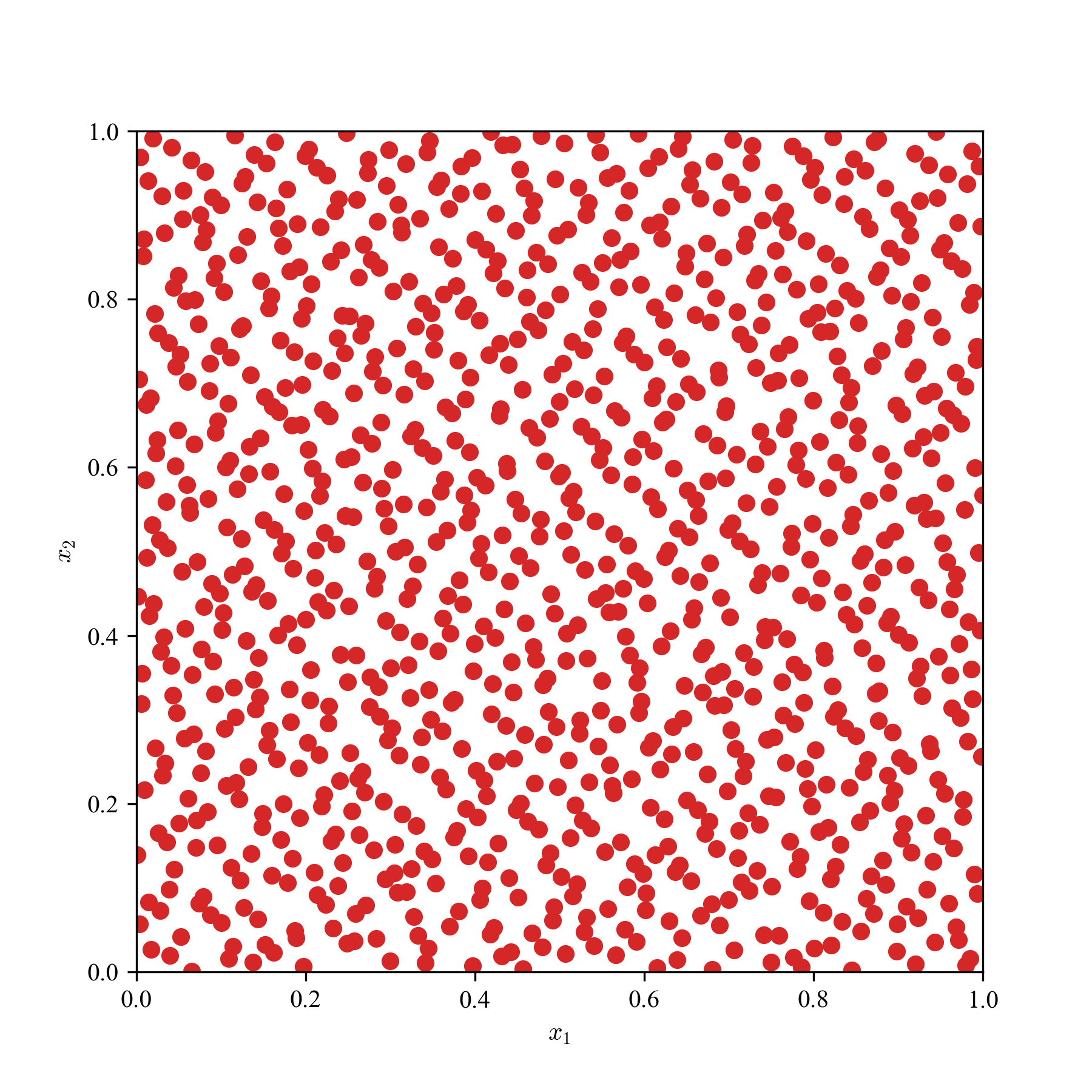 |
Sobol'列とHalton列は,乱数の癖に,超一様っぽさがあり,準乱数らしさが見て取れる.
円周率の近似
最も代表的な実験は,円周率$\pi$の近似であろう.
2次元($d = 2$)では,$[0, 1]^2$に一様乱数を散撒き,単位円(の$1/4$の領域)に入る点の個数で以て$\pi$を近似する.これには,半径$r$の円の面積$S$が$S = \pi r^2$で求まることを利用している.
また,3次元($d = 3$)では,$[0, 1]^3$に一様乱数を散撒き,単位球(の$1/8$の領域)に入る点の個数で以て$\pi$を近似する.これには,半径$r$の球の体積$V$が$V = \frac{4}{3} \pi r^3$で求まることを利用している.
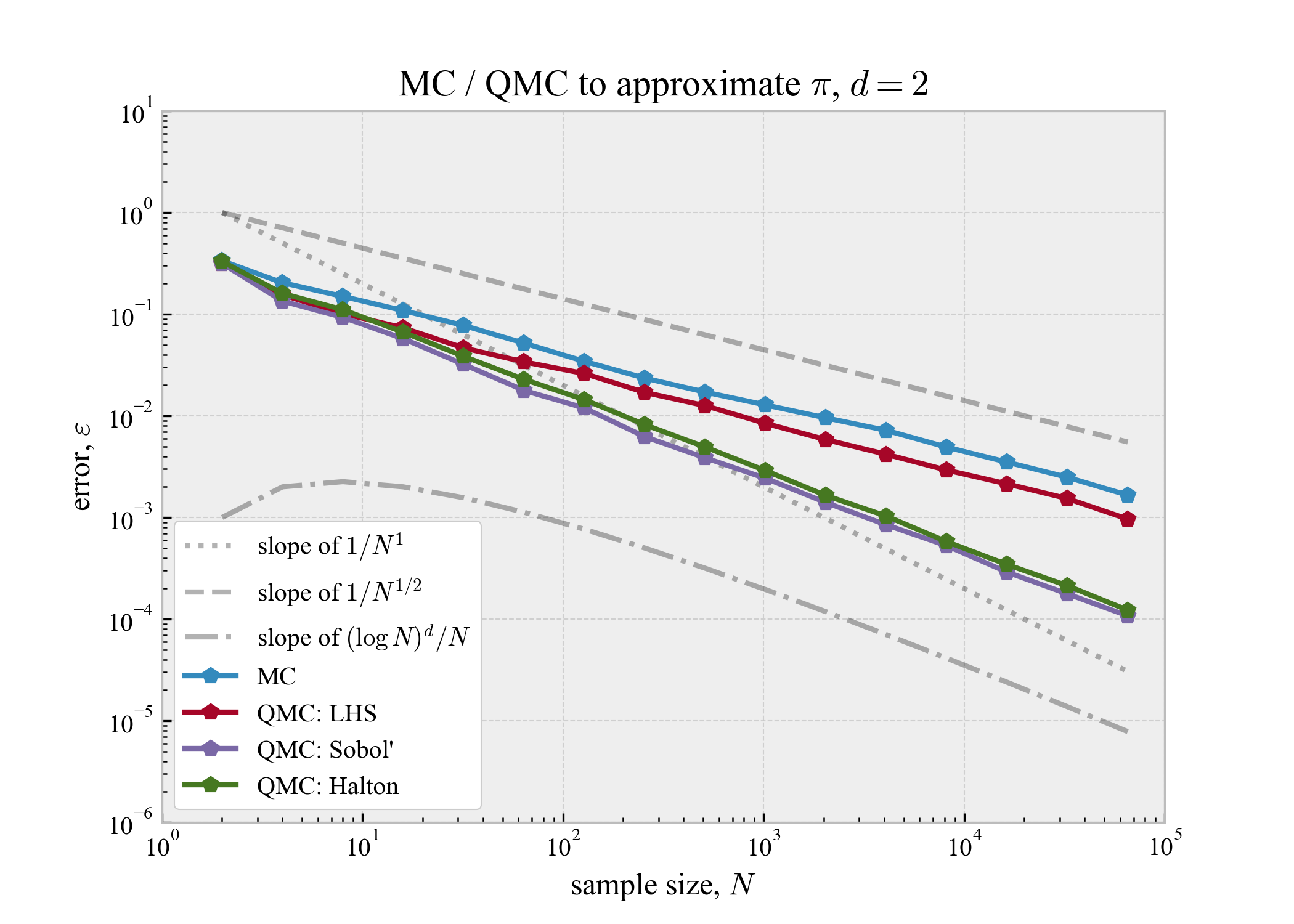
標本サイズ$N$と近似誤差$\varepsilon$の関係は以下のようになった.標本サイズは2の冪で増やしたが,プロットは底10の対数が解釈し易いと思ったので,そうしている.
| $d=2$ | $d=3$ |
|---|---|
 |
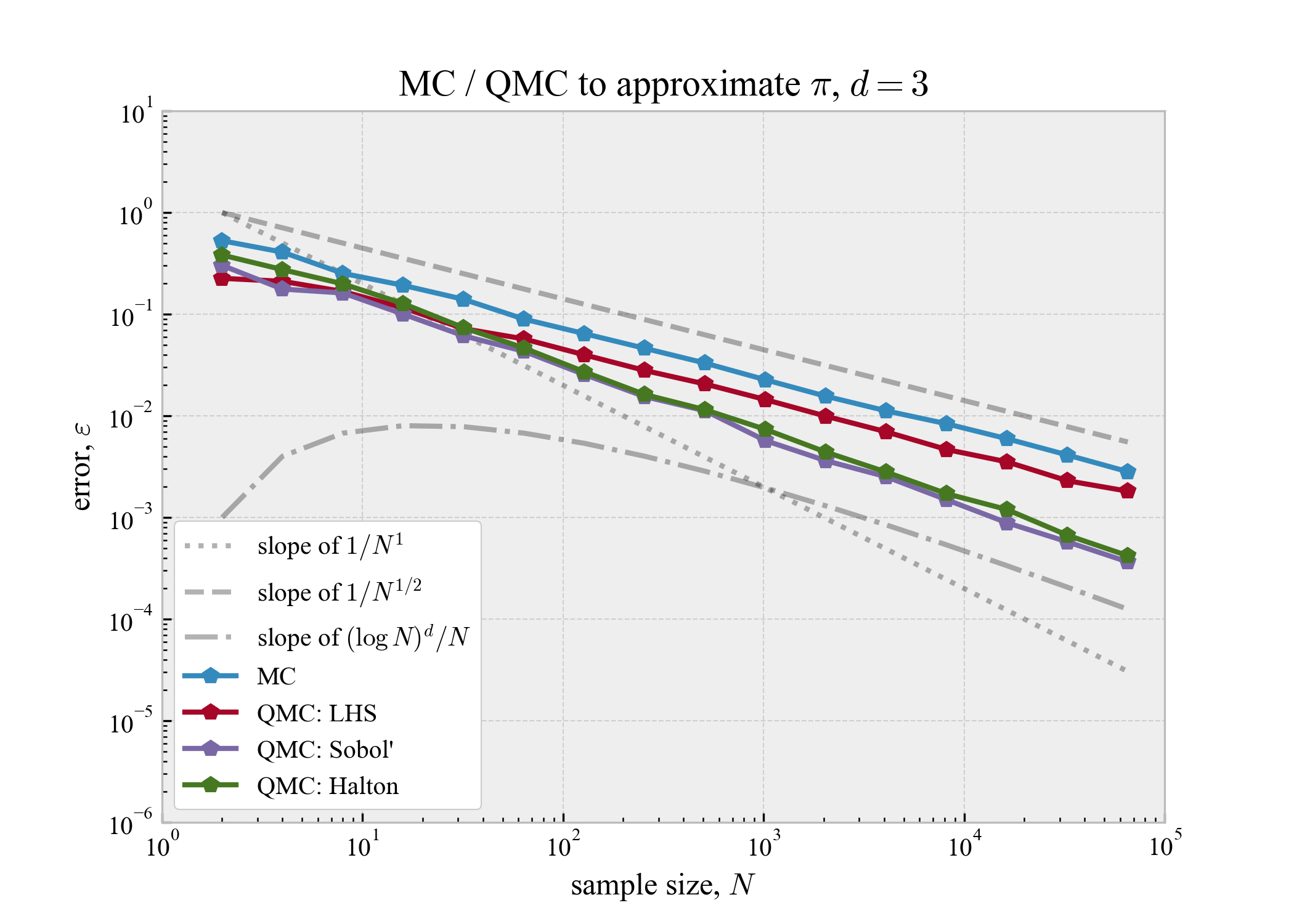 |
$d = 2$の結果を見ると,MCは凡そ$1 / \sqrt{N}$程度の速度で誤差が収束しているように見える.LHSはMCと同等の速度しか出ていない.Sobol'列,および,Halton列は$1 / N$には届かないもののMCより速く,$N$が十分大きいときに$(\log N)^d / N$程度で収束している.$d = 3$の結果は$d = 2$の結果と良く似ている.Sobol'列とHalton列は,$d$の増加に伴い収束速度が若干悪化しているが,まだMCより速いと言って良いだろうか.
積分の近似
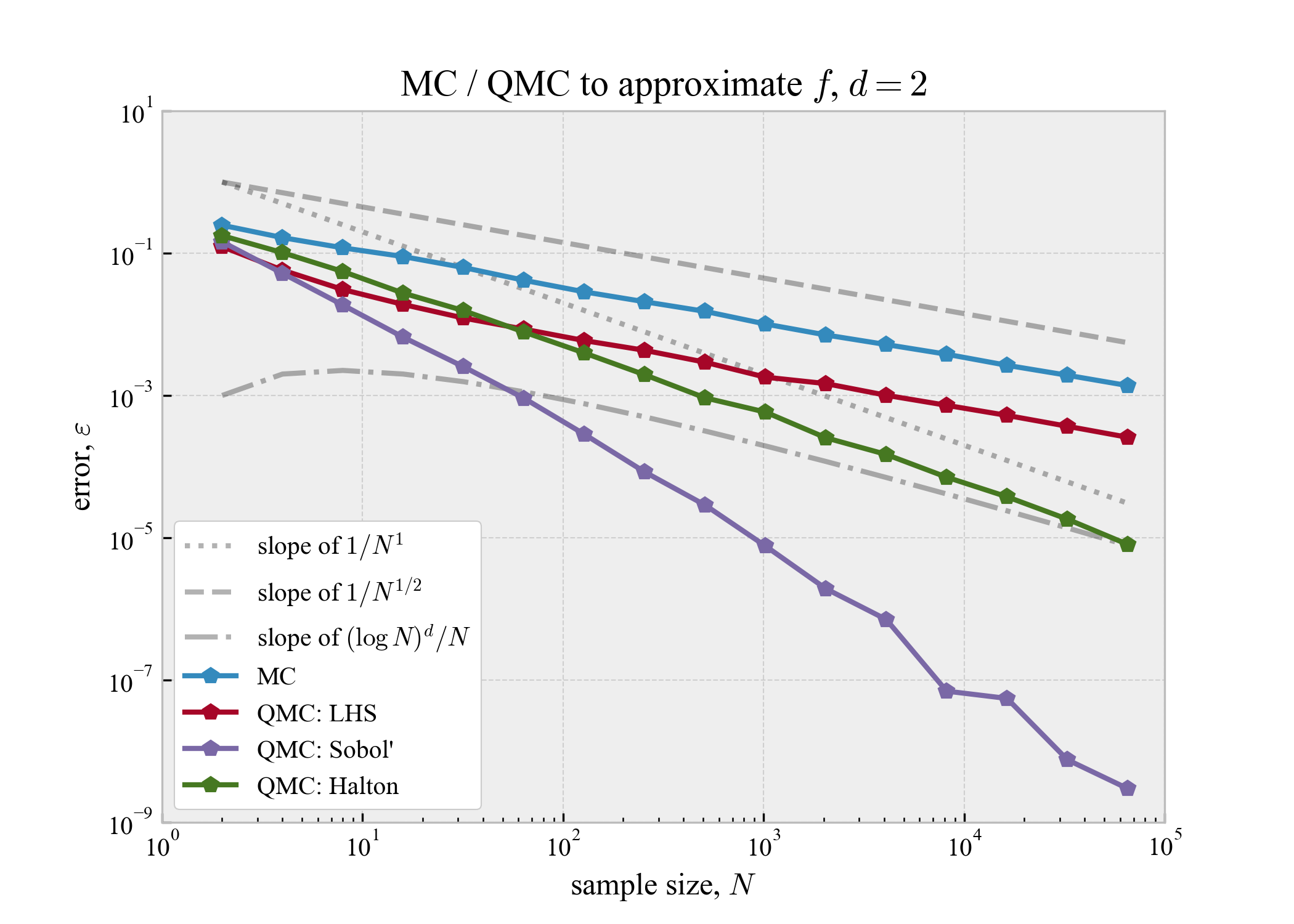
適当な関数の積分を近似してみる.鈴木&合田2020に倣い,$f = \exp(x_1 + x_2 + \cdots + x_d)$の$[ 0, 1 ]^d$での積分を近似することとする.
まずは,$d = 2, 3$で実験してみる.
| $d=2$ | $d=3$ |
|---|---|
 |
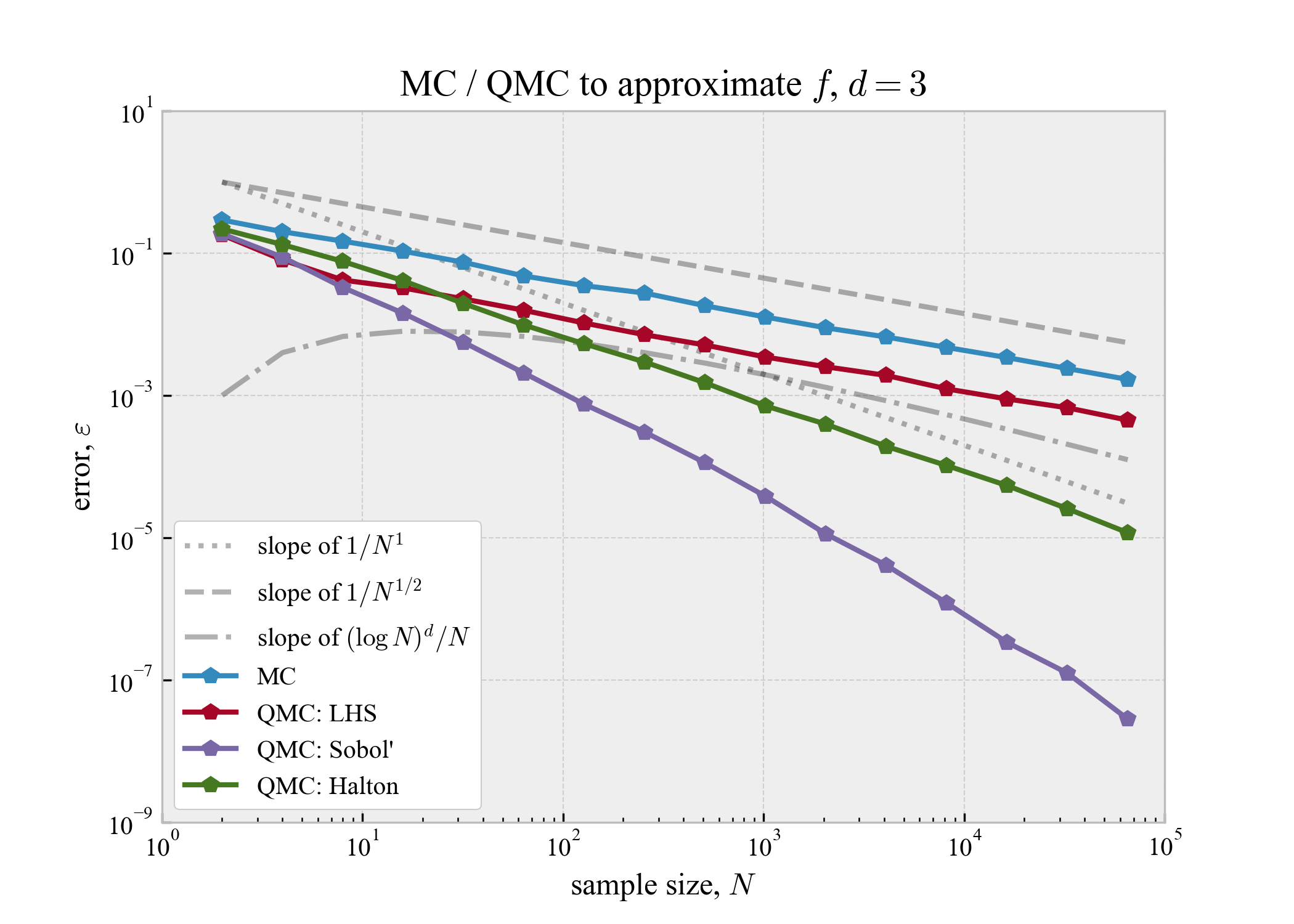 |
MC,LHSはどちらも$1 / \sqrt{N}$程度の収束速度を持っているように見える.Halton列は$1 / N$程度の速度が出ている.また,Sobol'列は$1 / N$以上の速度が出ているような気がする.
続いて,$d = 10, 20$で実験してみる(縦軸の変化に注意).
| $d=10$ | $d=20$ |
|---|---|
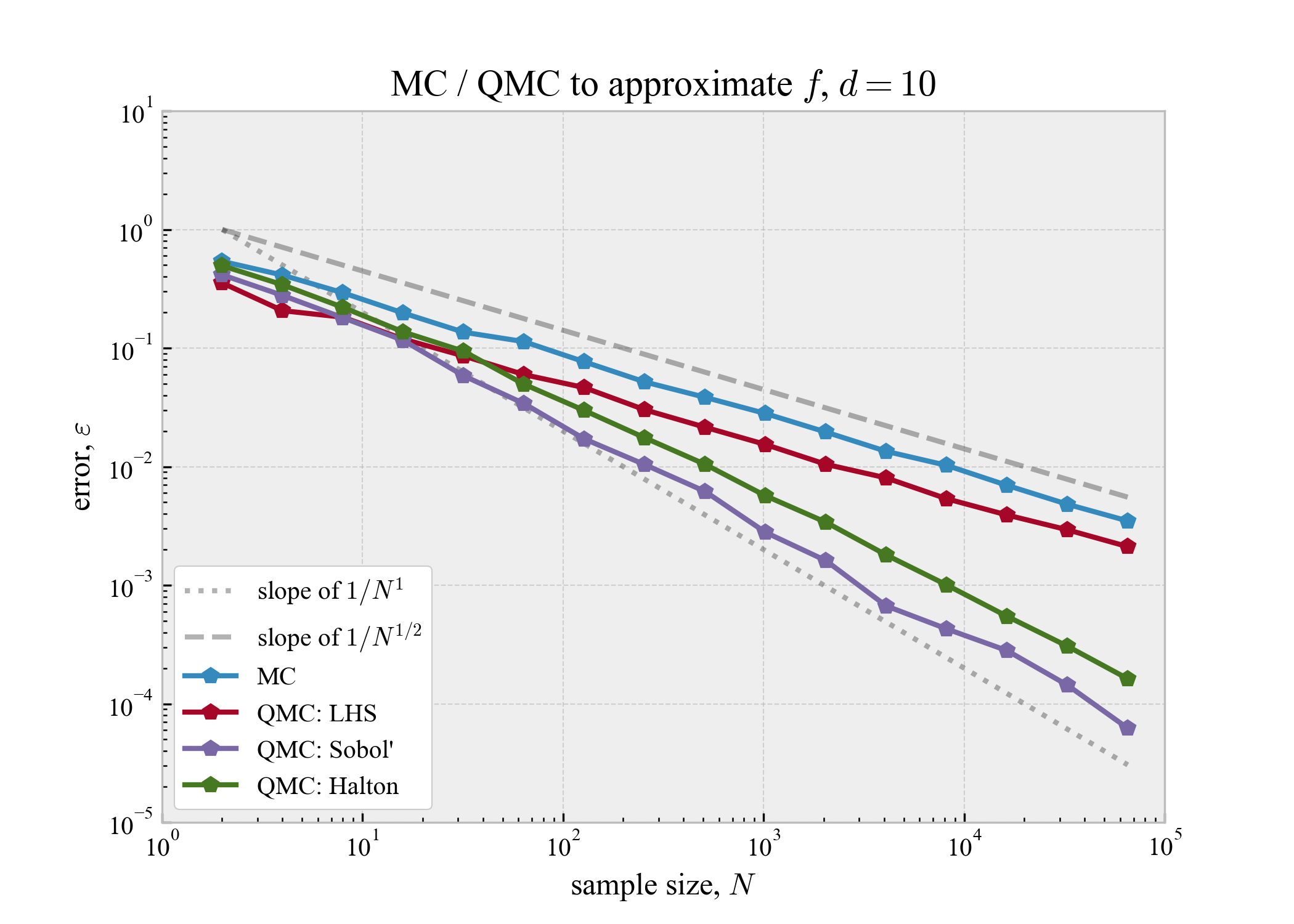 |
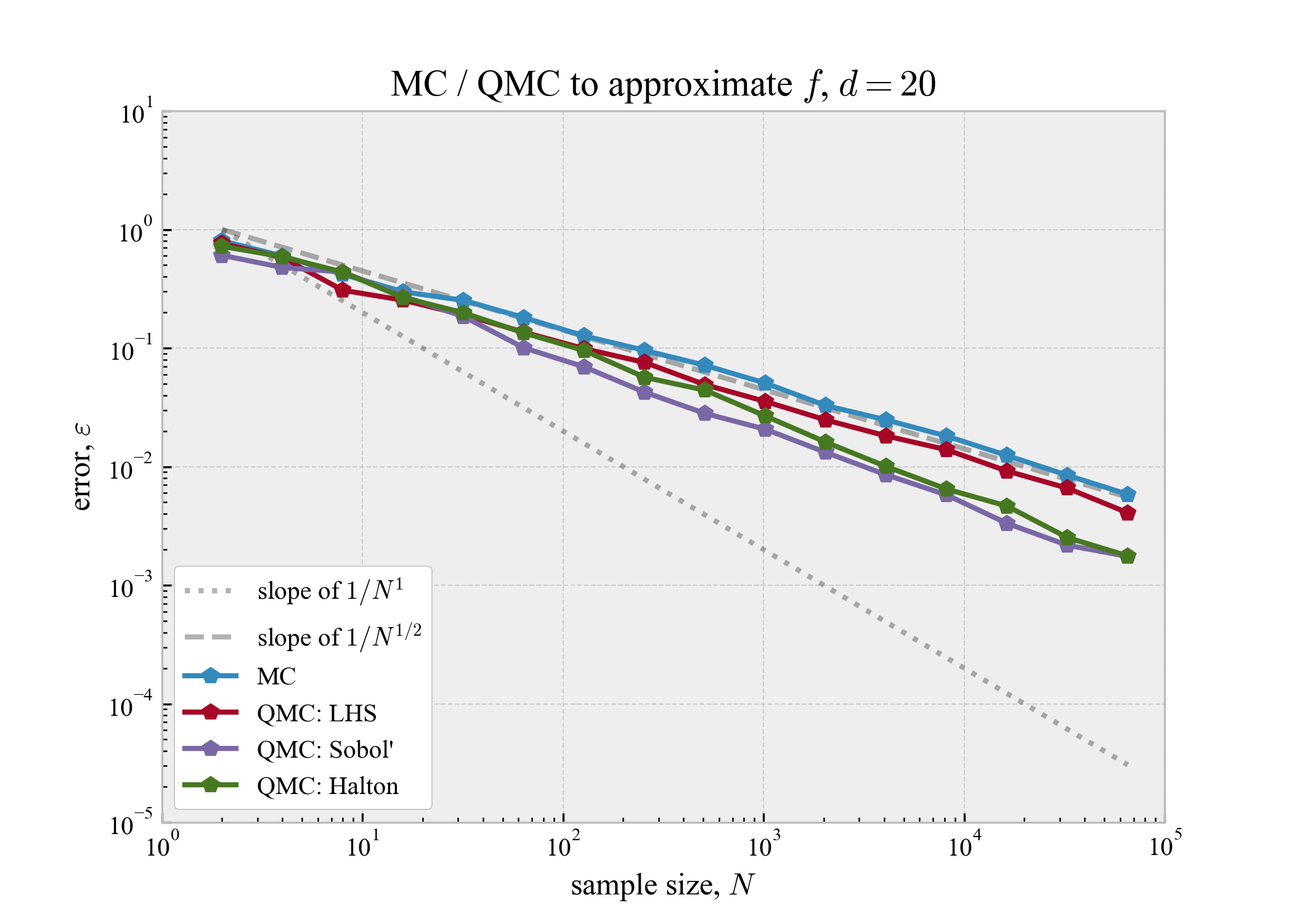 |
次元が低いときと比較すれば収束性は悪くなっているが,それでもSobol'列やHalton列がMCより良い性能を発揮していることが分かる.また,やはりLHSはMCと同等の収束性のようだ.
$d = 2, 3$の実験結果が,鈴木&合田2020の結果とは傾向が異なるのが気になるが,$d = 10, 20$での結果は凡そ合致していると言って良いだろう.取り敢えず,Sobol'列が良い収束性を示すという主張は通りそうだ.
終わりに
幾つかの実験から,MC / QMCの収束速度を観察した.鈴木&合田2020の報告とは若干傾向の異なる実験結果を得たが,鈴木&合田2020の言う通り,「まずSobol'列によるQMCを試す」べきという主張は通りそうな結果であった.
LHSは意外にもMCと変わらないということが分かった.もう少し良いと思っていたので,知らないことを知れて良かった.また原因を勉強していきたい.
MCは等重み求積法であると解釈できるから,求積法との繋がりを考えてみようと思っていたが,既に議論されていた.