概要
JuliaからWolfram Engine (or Mathematica)を呼び出して種々の計算を行う例を紹介します。例えば以下のような用途を想定しています。
- マニアックな特殊関数を使いたい
- 解析的に実行はできるが、表式がものすごく複雑になる積分をJuliaで実装したい
サンプルコードはGistで公開しています。
準備
Juliaは導入済みであるとします。
- Wolfram Engineをこちらのサイトからダウンロードしてインストールします。
- Juliaを立ち上げ、
MathLink.jlパッケージを導入します。
(注意)MathLink.jlのビルドに成功しても、手動でパスの設定をしなくてはならない場合がある模様です。私の場合、以下で説明するwevalの初回実行時に"choose a MathLink program to launch"というウィンドウが立ち上がり、そこでMathKernel.exeを選択することで使用できました。
検証環境は以下の通りです。
- OS: Windows 10
- Wolfram Engine 13.0
- Julia 1.5.3
- MathLink v0.3.2
使用例
W""もしくはW``というマクロを定義し、それをweval関数に渡すと、渡した内容がWolfram Engineで実行されます。
式の評価
まずは公式ページのサンプルコードを動かしてみます。$\sin x$ を記号的に定義し、その後 $x=1$ を代入するコードです。
julia> using MathLink
julia> sinx = W"Sin"(W"x")
W"Sin"(W"x")
julia> weval(sinx, x=1)
W"Sin"(1)
julia> weval(sinx, x=1.0)
0.8414709848078965
この例のようにx=1と整数を代入した場合は、記号的な式が維持されます。数値を得たいときはx=1.0にように実数を渡せばOKです。
この他W``を使う方法もあります。この場合、バッククォートの中にはWolfram Engineに実行させたいコードをそのまま書きます。
julia> sinx = W`Sin[x]`
W"Sin"(W"x")
julia> weval(sinx, x=1)
W"Sin"(1)
julia> weval(sinx, x=1.0)
0.8414709848078965
ちなみにギリシャ文字も使えます。
julia> fα = weval(W`α^2`)
W"Power"(W"α", 2)
julia> weval(fα, α=2)
4
複素数
計算結果が複素数 $a + ib$ の場合、wevalの戻り値はW"Complex(a, b)"のようになります。これをJuliaの複素数型に自動で変換する機能は現段階ではないように見えます。自前でやるには以下のようにすれば良いと思います。
julia> z = weval(W`2.0 - 1.0I`)
W"Complex"(2.0, -1.0)
julia> z.args
2-element Array{Float64,1}:
2.0
-1.0
julia> z.args[1] + 1.0im * z.args[2]
2.0 - 1.0im
zをtypeofで調べるとMathLink.WExpr型になっていることが分かり、調べてみるとこの型はargsという値を持つことが分かります。argsの中身は2成分配列になっており、第一成分に実部、第二成分に虚部が格納されています。これらを手で取り出してやればJuliaの複素数に翻訳できます。
特殊関数
$\sin x$ などと同様の書式で書けばOKです。
julia> weval(W"BesselK"(1/4, 1))
0.4307397744485861
julia> weval(W"Hypergeometric2F1"(2, 3, 4, 5))
W"Times"(W"Rational"(3, 500), W"Plus"(15, W"Times"(W"Complex"(0, 8), W"Pi"), W"Times"(8, W"Log"(4))))
julia> weval(W"Hypergeometric2F1"(2., 3., 4., 5.))
W"Complex"(0.1565421293337546, 0.15079644737231002)
積分
不定積分 $\int \sin x dx$ を計算し、結果に$x=1$を代入するコードは次のように書けます。
julia> fx = weval(W"Integrate"(sinx, (W"x")))
W"Times"(-1, W"Cos"(W"x"))
julia> weval(fx; x=1.0)
-0.5403023058681398
定積分 $\int_0^1 \sin x dx$ のサンプルコードです。数値を得たい場合は積分範囲を実数にするか、NIntegrateを使います。
julia> weval(W"Integrate"(sinx, (W"x", 0, 1)))
W"Plus"(1, W"Times"(-1, W"Cos"(1)))
julia> weval(W"Integrate"(sinx, (W"x", 0., 1.)))
0.4596976941318603
julia> weval(W"NIntegrate"(sinx, (W"x", 0, 1)))
0.4596976941318603
広義積分 $\int_{-\infty}^{\infty} \exp(-x^2/2)$ のサンプルコードです。無限大はW"Infinity"とすれば良いのですが、実は$-\infty$の方が曲者です。ここではバッククォートマクロで書きました。
julia> gauss = W`Exp[-x^2/2]`
W"Exp"(W"Times"(W"Times"(-1, W"Power"(W"x", 2)), W"Power"(2, -1)))
julia> res = weval(W"Integrate"(gauss, (W"x", W`-Infinity`, W`Infinity`)))
W"Power"(W"Times"(2, W"Pi"), W"Rational"(1, 2))
julia> res == weval(W`Sqrt[2 Pi]`)
true
最後に応用例です。積分で定義される関数に対し、それをWolfram Engineで計算し、結果を描画します。例として次の関数を考えます。
$$ Z(\lambda) = \int_{-\infty}^{\infty} \exp(-x^2/2 - \lambda x^4/4) $$
integrand = W`Exp[-x^2/2 - λ x^4/4]`
Zλ = weval(W"Integrate"(integrand, (W"x", W`-Infinity`, W`Infinity`)))
Z(λ) = weval(Zλ, λ=λ)
ちなみにこの積分結果は
$$ Z(\lambda) = \frac{1}{\sqrt{2\lambda}} \exp\Big(\frac{1}{8\lambda}\Big) K_{1/4}\Big(\frac{1}{8\lambda}\Big) $$
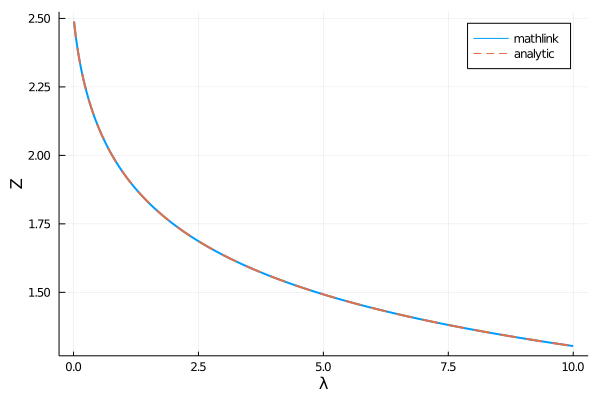
です。両者を描画してみると、
using SpecialFunctions
using Plots
ExactZ(λ) = 1/(sqrt(2λ)) * exp(1/(8λ)) * besselk(1/4, 1/(8λ))
begin
λs = 0.01:0.01:10
plot(λs, Z.(λs), lw=2, label="mathlink")
plot!(λs, ExactZ.(λs), ls=:dash, lw=2, label="analytic")
xlabel!("λ")
ylabel!("Z")
end
となります。