ハイブリッドモンテカルロ法とは
ハイブリッドモンテカルロ (Hybrid Monte Carlo) 法、略してHMC法とは、かなり一般的な確率密度関数 $P$ について、対応する確率変数を生成することができるアルゴリズムです。具体的には、平衡分布が $P$ であるような性質の良いマルコフ連鎖を構成することによってこれを実現します。
以下ではJuliaでHMCを実装し、これを多重積分の数値計算に応用する方法を紹介します。この手法の理論的な正当化などに興味がある方は、末尾の参考文献を御覧ください。
モンテカルロ数値積分
もともとHMC法は、クォーク、グルーオンという素粒子の性質を調べるために開発された手法です。この問題の技術的な内容は、数百万重積分を数値的に計算するというもので、多くの場合モンテカルロ法によって行われます。
$O$ を適当な関数とし、$0 \leq P \leq 1$ であると仮定します。このとき、
I = \int dx_1 dx_2 \dots dx_n O(x_1,x_2,\dots,x_n) P(x_1,x_2,\dots,x_n)
の形をした積分は、
I = \frac{1}{N} \sum_{j=1}^N O(X_1^j,X_2^j,\dots,X_n^j) + \mathcal{O}(1/\sqrt{N})
と近似することができます。ここで、$X_1^j,X_2^j,\dots,X_n^j$ は $P$ に従う確率変数で $X_k^j$ と $X_k^{j'}$ $(j \neq j')$ は独立であるとします。この確率変数を発生させる際にHMCが利用できます。
HMC法のアルゴリズム
以下では、$P$ として
P(x_1,x_2,\dots,x_n) \propto e^{-S(x_1,x_2,\dots,x_n)}
という関数形を仮定します。一般に、$P \propto fe^{-S}$ というタイプの確率密度関数は、$e^{-S+\log f}$ と書き直して $S-\log f$ を新たに $S$ と読み替えることで、上の形に帰着します。
次に、以下のような連立微分方程式
\begin{align}
\frac{dx_i(t)}{dt} &= \frac{\partial H}{\partial p_i(t)} = p_i(t) \\
\frac{dp_i(t)}{dt} &= -\frac{\partial H}{\partial x_i(t)} = -\frac{\partial S}{\partial x_i(t)}
\end{align}
を考えます。ここで $H$ は
H(p_i,x_i) = \frac{1}{2}\sum_{i=1}^n p^2_i + S(x_1,x_2,\dots,x_n)
で与えられるものとします。$H$ をハミルトニアンと呼び、上の微分方程式をハミルトン系とか運動方程式などと呼びます。
この方程式を、適当な $x_i(0)$ とランダムに発生させた $p_i(0)$ を初期条件として $t=0$ から $t=1$ まで解き、得られた $x_i(1)$ をサンプリングするという手順を繰り返すことで、所望のマルコフ連鎖が得られます1。ハミルトン系を用いるという点から、この手法のことをハミルトニアンモンテカルロ (Hamiltonian Monte Carlo) 法と呼ぶ流儀もあります。
ただし、これを計算機上で実現するためには、運動方程式を適切なスキームで離散化して解き、なおかつメトロポリステストと呼ばれる操作を行って、数値誤差の影響を補正する必要があります。このことを念頭においた上で具体的なアルゴリズムを書き下すと、以下のようになります。
ステップ 0)
$x_i(0)$ を適当にセットする。
ステップ 1)
$p_i(0)$ を標準正規分布に従って発生させる。
ステップ 2)
運動方程式を $t=0$ から $t=1$ まで解く。時間刻み幅を $\Delta t = 1/N_t$ とおく。$x_i(l\Delta t) = x_i^{l}$, $p_i(l\Delta t) =p_i^{l}$ と略記する。離散化された運動方程式は以下で与えられる2。
\begin{align}
p_i^{1/2} &= p_i^0 - \frac{1}{2}\frac{\partial S}{\partial x_i^0} \Delta t \\
%
x_i^{k+1} &= x_i^k + p_i^{k+1/2} \Delta t \\
p_i^{k+3/2} &= p_i^{k+1/2} - \frac{\partial S}{\partial x_i^{k+1}} \Delta t \\
%
x_i^{N_t} &= x_i^{N_t-1} + p_i^{N_t-1/2} \Delta t \\
p_i^{N_t} &= p_i^{N_t-1/2} - \frac{1}{2}\frac{\partial S}{\partial x_i^{N_t}} \Delta t \\
\end{align}
ここで、$k = 0,1,\dots,N_t-2$.
ステップ 3)
$r$ を区間 $[0,1]$ の一様分布に従って発生させた確率変数とする。
$r$ が不等式
\begin{align}
r < \mathrm{min}\{ 1, e^{-\Delta H}\}, \quad
\Delta H =
H(p_i^{N_t},x_i^{N_t})-H(p_i^0,x_i^0)
\end{align}
を満たすとき、$x_i^{N_t}$ をサンプリングし、これを新たに $x_i^0$ とする。満たさなかった場合はなにもしない。
**ステップ 1)-3)**を繰り返す。
Juliaで実装
前節で述べたアルゴリズムをコードにすると、以下のような形になります。Nsampleはサンプル数を表します。またseedは乱数のシード値を表します。乱数を使う数値計算では、結果の再現性を確保するために、シード値を明示的に指定するようにします。
using Random, Random.DSFMT, Distributions
function hybrid_montecarlo(S, ∇S, n, Nt, Nsample, seed)
# step 0
rng = MersenneTwister(seed)
x = zeros(n)
conf = zeros(n, Nsample)
isample = 1
while isample < Nsample+1
# step 1
p = rand(rng, Normal(), n)
# step 2
Hini = 0.5*sum(p.*p) + S(x)
p, x_trial = hamilton_dynamics(p, x, Nt, ∇S)
Hfin = 0.5*sum(p.*p) + S(x_trial)
# step 3
ΔH = Hfin - Hini
if rand(rng) < minimum([1.0, exp(-ΔH)])
x = x_trial
conf[:, isample] = x
isample += 1
end
end
return conf
end
ステップ 1のところでは、Distributionsパッケージを使って、rand(rng, Normal(), n) とすることで標準正規分布に従う乱数を発生させています。
ステップ 2のhamilton_dynamicsは運動方程式を解かせる部分で、これは以下のように書けます。∇S(x)はベクトル $(\frac{\partial S}{\partial x_1},\dots,\frac{\partial S}{\partial x_n})$ を返す関数とします。
function hamilton_dynamics(p, x, Nt, ∇S)
Δt = 1.0/Nt
p -= 0.5Δt * ∇S(x)
for k in 1:Nt
x += Δt * p
p -= Δt * ∇S(x)
end
x += Δt * p
p -= 0.5Δt * ∇S(x)
return p, x
end
数値積分への応用
以下では、
\langle O \rangle \equiv \frac{\int \prod_{i=1}^n dx_i O(x_1,\dots,x_n) e^{-S(x_1,\dots,x_n)}}{\int \prod_{i=1}^n dx_i e^{-S(x_1,\dots,x_n)}}
という量をモンテカルロ法によって計算します。
\frac{e^{-S(x_1,\dots,x_n)}}{\int \prod_{i=1}^n dx_i e^{-S(x_1,\dots,x_n)}}
が確率密度関数の役割をします。以下の数値計算の結果はJulia 1.4.0で行いました。
ガウス積分
まずは
S = \frac{1}{2} \sum_{i=1}^n x_i^2, \quad
O = \frac{1}{n} \sum_{i=1}^n x_i^2.
の場合をやってみます。$n$ が大きくても単なるガウス積分ですので、積分は厳密に実行できて $\langle O \rangle = 1$ となります。以下は $n=100$ の計算例です。
S(x) = sum(x.^2/2)
∇S(x) = x
O(x) = sum(x.^2)/length(x)
n = 100
Nt = 100
Nsample = 10000
seed = 1
conf = hybrid_montecarlo(S, ∇S, n, Nt, Nsample, seed)
res = [O(conf[:, i]) for i in 1:Nsample]
@show mean(res), std(res)
実行結果は
(mean(res), std(res)) = (0.998356750101778, 0.1412414995491931)
となりました。統計誤差が案外大きいですが、厳密解とconsistentです。
HMCの注意点としては、運動方程式を解くときの時間刻み幅 $\Delta t$ が大きすぎると、ステップ 3) で配位 $x_i^{N_t}$ が採択される確率が低下するという点が挙げられます。この現象は、$\Delta H$の値が大きくなりすぎる(離散化誤差のためにエネルギー保存則が大きく破れている)ために発生します3 。
例えば Nt = 5 ($\Delta t = 0.2$) とすると、10000回中377回配位の採択がrejectされました。この程度であれば実用上問題になりませんが、あまりにも頻繁にrejectされる場合は検討が必要です。適切な $\Delta t$ の大きさは問題の詳細に依存するので、ある程度try and errorで決めざるを得ない場合があります。
0次元BCS模型
次に、もう少し現実的な例として、以下のようなtoy modelを考えます。
\begin{align}
S &= \frac{1}{2}\sum_{i=1}^n \phi_i^2 - 2\log \left( e^{n\mu + \sqrt{g} \sum_{i=1}^n \phi_i} + 1 \right) \\
%
O &= \frac{1}{e^{-n\mu - \sqrt{g} \sum_{i=1}^n \phi_i} + 1}
\end{align}
ここで、$\mu$ は実数、$g$ は正の定数です。この出どころは、超伝導のBardeen-Cooper-Schrieffer (BCS) 模型において、フェルミオンの質量を無限大に取ったものです。$O$ の期待値は粒子数密度に対応し、その厳密な値は
\langle O \rangle = \frac{e^{2\beta\mu+2\lambda} + e^{2\beta\mu+\lambda/2}}{e^{2\beta\mu+2\lambda} + e^{2\beta\mu+\lambda/2} + 1}
で与えられます。ここで、$\beta=n$, $\lambda = \beta g$ とおきました4。
$S$ とその微分、$O$ をJuliaで書くと、次のようになります。厳密解と比較しやすいように、$βμ, λ$ を引数にとるように定義しておきます。
function bcs_S(φ, βμ, λ)
g = λ / length(φ)
sum(φ.^2/2) - 2log(exp(βμ+sqrt(g)*sum(φ)) + 1.0)
end
function bcs_∇S(φ, βμ, λ)
g = λ / length(φ)
φ .- 2.0*sqrt(g)/(exp(-βμ-sqrt(g)*sum(φ)) + 1.0)
end
function number_density(φ, βμ, λ)
g = λ / length(φ)
1.0/(exp(-βμ-sqrt(g)*sum(φ)) + 1.0)
end
以下は$\lambda$を固定し、複数の $\beta\mu$ について積分を計算するコードのサンプルです。
function sampling()
Nt = 100
n = 10
Nsample = 10000
seed = 1
βμ = -8:8
λ = 1.0
n_mean = zeros(length(βμ))
n_err = zeros(length(βμ))
for i in 1:length(βμ)
S(φ) = bcs_S(φ, βμ[i], λ)
∇S(φ) = bcs_∇S(φ, βμ[i], λ)
conf = hybrid_montecarlo(S, ∇S, n, Nt, Nsample, seed)
res = [number_density(conf[:,j], βμ[i], λ) for j in 1:Nsample]
n_mean[i] = mean(res[:])
n_err[i] = std(res[:])
end
n_mean, n_err
end
次がその結果です。横軸が $\beta\mu$ 縦軸が $\langle O \rangle$, 実線は厳密解を表します。HMCの結果は厳密解をよく再現します。
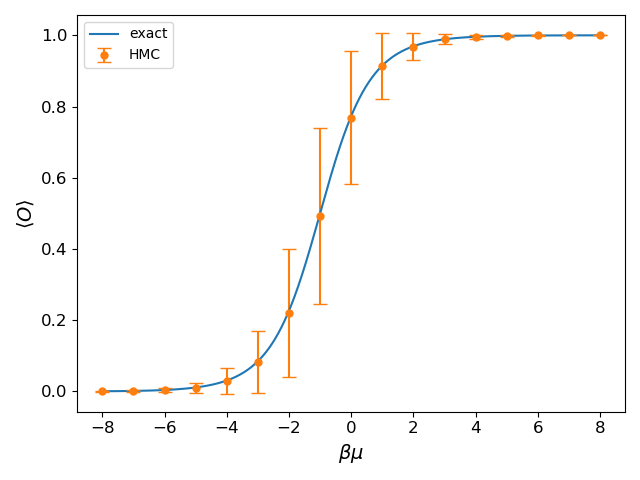
(2021/4/17追記)上の図では、エラーバーをstd(res[:])によってつけていますが、本来はstd(res[:])/sqrt(Nsample)とすべきでした。時間があるときに修正します。
ここで説明しなかったこと
-
より複雑な模型でHMCを行った場合、マルコフ連鎖が目標分布である$e^{-S}$に収束するまでに時間がかかります。この時間を熱平衡化時間と呼びます。(上の例では熱平衡化時間は無視できるほど短くなっています。)熱平衡化時間は、相異なる2つの初期条件のもとにHMCを行い、測定量に初期条件依存性が見えなくなるまでの時間によって見積もれます。
-
上のコードの通りに配位をサンプリングすると、一般には配位間に相関があり、独立な確率変数とはみなせません。このため本当は、$\langle O \rangle$ の値とその誤差をジャックナイフ法やブートストラップ法によって補正する必要があります。
-
確率密度関数が $fe^{-S}$ という関数形の場合、$f$ の零点の構造によっては、$x_i$ が動き回れる領域が2つ以上に分断されてしまい、正しいサンプリングが行えなくなることがあります。このようなときは、レプリカ交換モンテカルロ法などを用いる必要があります。
参考文献
- HMCの原論文: S. Duane, A. Kennedy, B. J. Pendleton, and D. Roweth, Physics Letters B 195, 216 (1987).
- 高エネルギー物理向けの教科書: 青木慎也著, 格子上の場の理論 (シュプリンガー現代理論物理学シリーズ)
- レビュー論文: D. Lee, Progress in Particle and Nuclear Physics 63, 117 (2009).
- 物性物理向けのレビュー論文: J. E. Drut and A. N. Nicholson, Journal of Physics G: Nuclear and Particle Physics 40, 043101
(2013). - 機械学習分野向けの教科書: C. M. Bishop, Pattern Recognition and Machine Learning (Springer)
- Juliaでは、MambaというパッケージからHMCが利用できるようです。ただし筆者は使ったことがないので、今の所これについてはコメントできません。
サンプルコードはGistで公開しています。
-
ハミルトン系の重要な性質として、$H(p_i(t), x_i(t))$ の値(エネルギー)が時間 $t$ によらず一定であるという点、時間反転対称性をもつという点があります。これらの性質のおかげで、マルコフ連鎖が詳細釣り合い条件を満たすことが示され、$P \propto e^{-S}$ が定常分布になることが保証されます。 ↩
-
いわゆる🐸飛び法(Leapfrog integration)と呼ばれるスキームです。これはシンプレクティック数値積分法の一種で、ハミルトン系を数値的に解くのに適しています。 ↩
-
$\Delta H$ のオーダーは $(\Delta t)^2$ となります。 ↩
-
$\beta$ は逆温度、$\mu$ フェルミオンの化学ポテンシャル、$g$ は引力の結合定数を表し、$\beta\mu$, $\lambda$ は無次元量になります。 ↩