はじめに
自身がデータ解析を行う上での注意点を書き残しておく用
- 解析を行う上でのTips
- 解析を行う上での注意点
<前情報>
今回はKaggleのコンペで使用されているデータを用いて説明します.
Kaggle House Prices DataSet
Kaggle House Prices Kernel
を用いてメモしておく.
Memo用に残しおくため, モデル精度などは気にしていないことをご了承ください
<データの中身>
特徴量は全てで81, このうちのSalePricesを目的変数( target )として解析を行います.
SalePrices以外を説明変数とします.
<更新日>
version2 : 2021.5.6
Tips
まずデータに対してこれだけは行っておくほうがいいこと
前処理
まず最初にデータ(DataFrame -> df)を読み込んで EDA (探索的データ解析) を行います.
- .head() : データの先頭の表示 , (5)であれば5行抽出, defalt値は5
- .info() : データの要約 (行数、列数、各列の列名、各列に格納されるデータの型 etc....)
- .describe() : データの基礎統計量 (min, max, 25% etc.....)
- .shape[0], .shape[1] : データの行数および列数の確認
- .columns : データのカラム名の取得
- .isnull().sum() : 各列の欠損地の個数確認
- .dtypes : 各列の型タイプを確認
# import
import pandas as pd
import matplotlib.pyplot as plt ## for drawing graph
## load Data
df = pd.read~~~~(csv , json etc...)
# データの先頭表示
df.head()
# データの要約表示
df.info()
# データの次元数(何行,何列)
print('There are {} rows and {} columns in df'.format(df.shape[0], df.shape[1]))
# データのカラム(列)取得
df.columns
# 各列データの欠損値の個数をカウント
df.isnull().sum()
# 各列データの型タイプ確認
df.dtypes
またデータ数が膨大な処理を行う場合,メモリ使用量を把握しておくほうが良い
print(f'Training Set Memory Usage: {df.memory_usage().sum() / 1024 ** 2:.2f} MB')
df.columnsでカラム名を取得することができますが, 型タイプに合わせたカラム名のリストを保持しておくことで, 後々のことを考えておくと利用できる可能性がある. 下記にそのコードを記載しておく.
includeを型タイプ(float64 etc...)に変更することも可能.
obj_columns = df.select_dtypes(include=['object']).columns
numb_columns = df.select_dtypes(include=['number']).columns
各型タイプごとにデータフレームを分割する場合
obj_df = df[obj_columns]
numb_df = df[numb_columns]
plot例
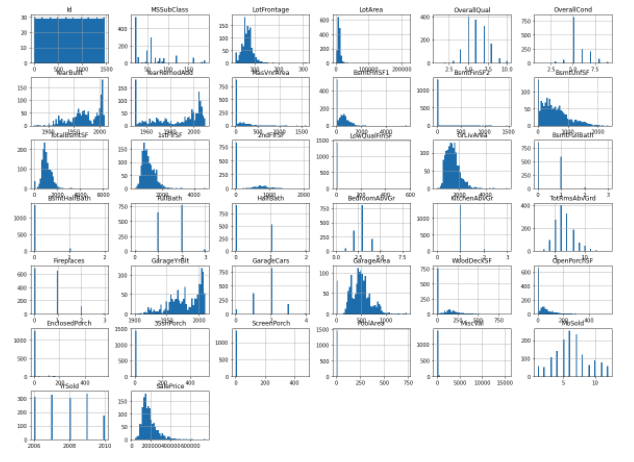
各列(特徴量)のヒストグラム
各列の特徴量をヒストグラム化する. しかしこれは数値データのみ取り扱うことができる. 文字列データに対しては適用できないため, それは後々記述する.
- .hist(bins=**, figsize=(,))
binsは頻度を分析する階級値の細かさの設定, figsizeは図の大きさの設定
他にも多くの引数をしてすることができるので, 下記を参照していただきたい.
official pyplot.hist document
df.hist(bins=50, figsize=(20,15))
plt.show()
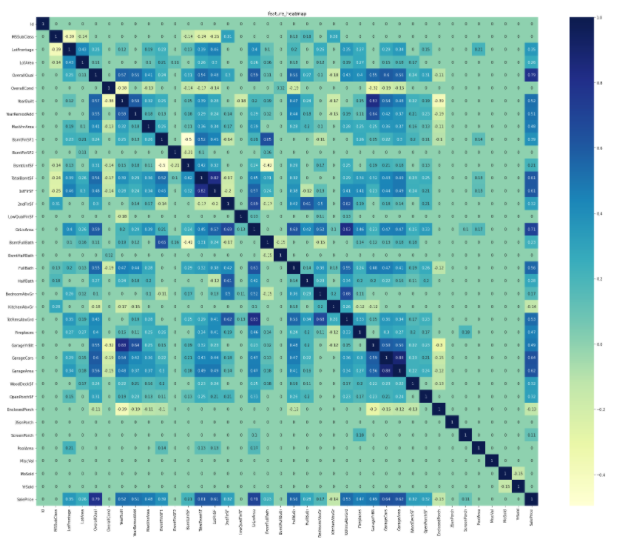
相関行列のヒートマップ
機械学習をする上で, 重要になってくるのが各特徴量の相関行列を求めることです. その相関行列の可視化を行うためのヒートマップで可視化する.
- .heatmap(corr, annot=bool(True or False), cmap='***')
corrは相関行列, annotはセルに値を設定, cmapは図のカラーを指定
他にも多くの引数をしてすることができるので, 下記を参照していただきたい.
official seaborn.heatmap document
import seaborn as sns ## for drawing graph
corr = train_df.corr()
corr[np.abs(corr) < 0.1] = 0 ## corr<0.1 => corr=0
sns.heatmap(corr, annot=True, cmap='YlGnBu')
plt.show()
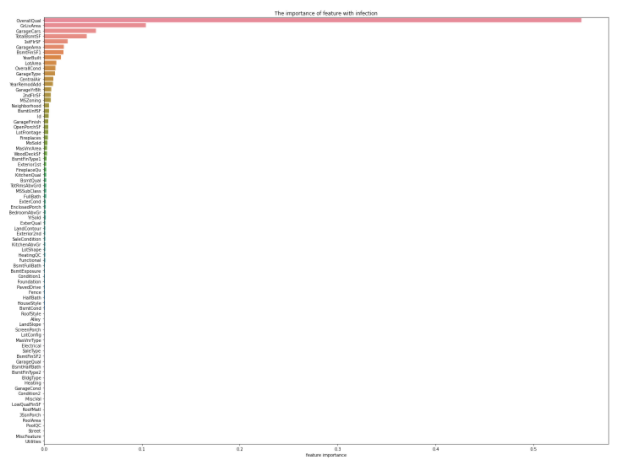
特徴量の重要度の推定
どの特徴量が, targetであるSalePricesにとって重要であるかをランダムフォレスト(RandomForest)を用いて算出する.
RandomForestを行うために, まず説明変数と目的変数に分割する必要がある.
今回はtarget(SalePsices)以外の変数を全て説明変数とする.
- .drop("***", axis=(0 or 1)) : ***には使用しない列を指定 , axis=0である場合は行, 1である場合は列
- RandomForestRegressor(n_estimators=**) : n_estimatorsは学習回数
from sklearn.ensemble import RandomForestRegressor
X_train = df.drop("SalePrices", axis=1)
y_train = df[["SalePrices"]]
rf = RandomForestRegressor(n_estimators=80, max_features='auto')
rf.fit(X_train, y_train)
ranking = np.argsort(-rf.feature_importances_) ##重要度が高い順に描画するため
sns.barplot(x=rf.feature_importances_[ranking], y=X_train.columns.values[ranking], orient='h')
plt.show()
各特徴量の分布(外れ値の確認用など)
回帰分析などを行う際に, 特徴量に外れ値が含まれている場合, モデルの精度に影響しやすいことが言われている. そのため, モデルの精度向上には外れ値処理が必須であると考えられている. そのために各特徴量には, どれくらいの外れ値が含まれているかを可視化して確認することがわかりやすい.
ここでは, 特徴量の重要度上位30位までのplotを行う.
- .iloc[:,:] : 行あるいは列を指定することで値を抽出
- sns.regplot : 2次元のデータと線形回帰モデルの結果を重ねてplot
X_train = X_train.iloc[:,ranking[:30]]
fig = plt.figure(figsize=(12,7))
for i in np.arange(30):
ax = fig.add_subplot(5,6,i+1)
sns.regplot(x=X_train.iloc[:,i], y=y_train)
plt.tight_layout()
plt.show()
注意点
target(目的変数)が正規分布にしたがっているかどうかの確認
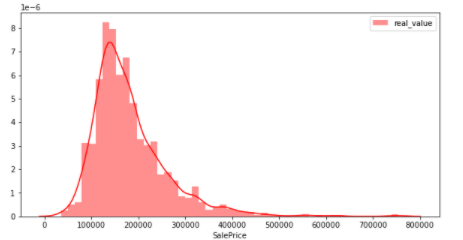
今回のデータではtargetはSalePricesである. 機械学習を行うにあたって,目的変数が正規分布に従っているかどうかはモデルに影響するため重要とされています.そこでSalePricesの分布を見ていきます. この図は,縦軸は割合,横軸はSalePricesを示しています.
sns.distplot(y_train, color="red", label="real_value")
plt.legend()
plt.show()
上図から分布が少し左に偏っていることがわかる. 正規分布(グラフにしたときに数値の大半が中央に集中し、左右対称の釣り鐘型に「分布」するデータ)ではない.
そこで目的変数が正規分布に従うように,よく使われる対数変換および差分変換を下記に示します.
y_train2 = np.log(y_train)
y_train2 = y_train2.replace([np.inf, -np.inf], np.nan)
y_train2 = y_train2.fillna(0)
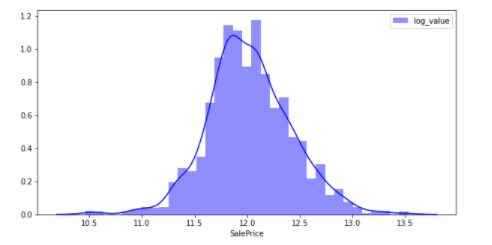
sns.distplot(y_train2, color="blue", label="log_value")
plt.legend()
plt.show()
対数変換を行うことで正規分布に近い図になっている.
y_train3 = y_train.diff(periods = 1)
y_train3 = y_train3.fillna(0)
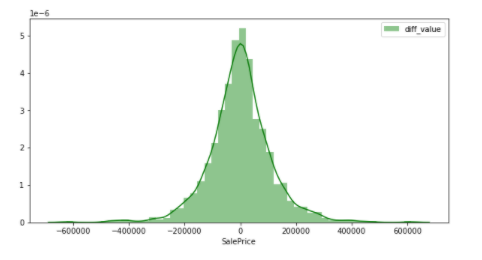
sns.distplot(y_train3, color="green", label="diff_value")
plt.legend()
plt.show()
差分変換を行うことで正規分布と言えるような図になっている.
つまり, モデルの精度に影響を与えにくいような目的変数は差分変換を行ったSalePricesであることが推測できる.
このように, どのデータを取り扱う時でも,値に偏りがないかどうかを確認しておいた方が良い.
実際に正規分布に従っている場合と従っていない場合のモデルの精度の比較を今後記事にしたいと思います.
まとめ
上記がデータ解析を行う上で, まず行うことのまとめである.
今後はデータ解析を行う上で, 先ほど述べていた文字列データの取り扱いや, 時系列データの取り扱いなどを記事にしたいと考えます.