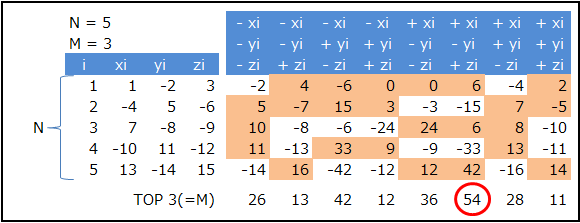始めに
競技プログラミングサイトAtCoder にて、ソート が あると便利な問題 を COBOL で解きました。
先の記事にて、クイックソートを実装しました。
https://qiita.com/ShinjiSHIBATA/items/1ef8cbf4b87969a46015
プログラミング言語 には 多くの場合 ソート が備わっている為 使うと ラク ができます。
「OpenCOBOL」「opensourceCOBOL」にも ソート があるので この記事に書きました。
1. 配列
COBOLでは 変数 や 配列 を「WORKING-STORAGE SECTION」に書きます。
WORKING-STORAGE SECTION.
01 var PIC 9(1).
01 card1.
03 card_num1 PIC 9(3).
03 card_num2 PIC 9(3).
03 card_num3 PIC 9(3).
~ 中略 ~
03 card_num10 PIC 9(3).
ここで「01」や「03」は レベル番号 と 呼ばれます。
最上位「01」は レコード と 呼ばれます。
レベル番号 で データ構造 の 従属関係 を表現します。
「var」は レコード で 符号なし 数字 1 桁 の 変数。
「card1」は レコード で その従属項目として card_num1 ~ card_num10 の
10項目 の 符号なし 数字 3 桁 があります。
同じ属性 の 繰り返し を表現したものが 配列 になります。
01 card1.
03 card_num PIC 9(3) OCCURS 10 TIMES.
要素数 10 の 配列 ができました。
要素 の 7 番目 は card_num(7) で表現されます。
次に 複数項目 の 繰り返し を表現した 配列 も 定義できます。
01 card1.
03 card11 OCCURS 10 TIMES.
05 card_num PIC 9(3).
05 card_color PIC X(10).
要素数 10 の 配列 で 2つ の項目があります
card_num 符号なし 数字 3 桁
card_color 文字 10 個 の 文字列
要素 の 7番目 は card_num ( 7 ) や card_color ( 7 ) で表現されます。
2. ABC 088 B Card Game for Two を解く
【問題概要】
N 枚のカード、i 番目のカードには ai という数が書かれています。
2 人が交互に最大の数のカードを取ります。取った数の合計が点数になります。
すべてのカードを取り終わった時、先手は後手より何点多く取るでしょうか。
【説明】
カード を並び替えて 大きな数 から
先手の取った数の 合計、後手の取った数の 合計 を計算します。
カードを並び替えるクイックソートを実装しました。
実際の問題の Accepted なソースコードは下記になります。
https://beta.atcoder.jp/contests/abc088/submissions/2765069
行数を数えると 167 行。
「OpenCOBOL」「opensourceCOBOL」の ソート を使って もっと ラク をしましょう。
「OpenCOBOL」「opensourceCOBOL」の ソート の概要は下記の通りです。
【構文どおり】
01 card1.
03 card PIC 9(3) OCCURS 100 TIMES DEPENDING ON N.
SORT card ON DESCENDING KEY card.
ソート の部分は 配列の定義の 2 行 を含めて たったの 3 行 です。
「DEPENDING ON N」を説明します。
配列は 最大 100 回 の 繰り返し項目です。要素数 100 です。
実際に配列に値が入っている (先頭からの) 要素の数は 変数 N の値によるという定義です。
ソート するのに 値が入っていない要素まで入れてしまうと結果がおかしくなる為
ソート する場合には 必ず指定します。
「SORT card ON DESCENDING KEY card」を説明します。
最初の「card」は OCCURS を指定した項目 (OCCURS項目) です。
「DESCENDING」は「降順」、「ASCENDING」は「昇順」です。
二番目の「card」は 実際にソートする時の キー項目 (KEY項目) です。
二回「card」が登場するところに違和感を感じるかもしれませんが
配列が複数の項目の場合には 最初 (OCCURS項目) と 二番目 (KEY項目) に指定する項目は
異なることがありますので必要となります。
ここで 昇順 ならば 「ASCENDING」が 省略できそうに思えますが
「DESCENDING」か「ASCENDING」は必ず指定する必要があります。
ここからさらに 省略した書き方 ができるので書きます。
【慣用的に略した書き方】
01 card1.
03 card PIC 9(3) OCCURS 100 DEPENDING N.
SORT card DESCENDING card.
配列定義の「TIMES」「ON」、ソートの「ON」「KEY」を 慣用的に省略することができます。
忘れても思い出せる感じが とても良い と思います。
「OpenCOBOL」「opensourceCOBOL」の ソート を使用した
実際の問題の Accepted なソースコードは下記になります。
https://beta.atcoder.jp/contests/abc088/submissions/2921407
行数 を数えると 69 行。
行数 59 % の削減に成功しました。
それだけ ソースコード の 見通しも良くなり バグ が少なくなります。
3. ABC 042 B Iroha Loves Strings (ABC Edition) を解く
【問題概要】
長さ L の 文字列が N 個あります。
これらの文字列を結合してできる文字列のうち 辞書順最小 を求めて下さい。
【説明】
要素数 N 個、文字 L 個 の 文字列 の 配列 に、文字列を格納して 昇順ソート します。
ソート後の文字列を順に結合することで 解答 となります。
「OpenCOBOL」「opensourceCOBOL」の ソート を使用した
実際の問題の Accepted なソースコードは下記になります。
https://beta.atcoder.jp/contests/abc042/submissions/2918629
4. ABC 018 A 豆まき (改) を解く
【問題概要】
長男、次男、三男が豆まきをしました。
長男、次男、三男の得点が順に与えられます。得点が高いほうが上の順位です。
長男、次男、三男のそれぞれの順位を答えて下さい。
※長男、次男、三男の得点は異なるのが実際の問題ですが
ここでは 同じ得点の場合は、長男よりも次男、次男よりも三男のほうが上の順位とします。
【説明】
以下のような配列を用意します。
要素数 3
num 符号なし 数字 1 桁
score 符号なし 数字 3 桁
rank 符号なし 数字 1 桁
num に 何番目の値か (長男なら 1 次男なら 2 三男なら 3)
score に 得点 を格納して ソート します。
この時のソートキーを以下のようにします。
複数キーソートです。
SORT mame DESCENDING score
DESCENDING num.
第 1 KEY項目 は score で 降順
第 2 KEY項目 は num で 降順
ソート後に 最初から 1 から順に rank に格納します。
次に num で 昇順ソートします。
ソート後に 順に rank を出力することで 解答 となります。
【ソースコード】
PROGRAM-ID. MAME.
DATA DIVISION.
WORKING-STORAGE SECTION.
01 N PIC 9(1).
01 i PIC 9(1).
01 val PIC 9(3).
01 mame1.
03 mame11 OCCURS 3 DEPENDING ON N.
05 num PIC 9(1).
05 score PIC 9(3).
05 rank PIC 9(1).
PROCEDURE DIVISION.
MOVE 3 TO N.
PERFORM VARYING i FROM 1 BY 1 UNTIL N < i
ACCEPT val
MOVE i TO num(i)
MOVE val TO score(i)
END-PERFORM.
SORT mame11 ON DESCENDING KEY score
ON DESCENDING KEY num.
PERFORM VARYING i FROM 1 BY 1 UNTIL N < i
MOVE i TO rank(i)
END-PERFORM.
SORT mame11 ON ASCENDING KEY num.
PERFORM VARYING i FROM 1 BY 1 UNTIL N < i
DISPLAY rank(i)
END-PERFORM.
STOP RUN.
【入力】
100
100
100
【出力結果】
3
2
1
5. ABC 100 D Patisserie ABC を解く
【問題概要】
N 種類 の ケーキ から 重複なしで M 種類 の ケーキ を 選びます。
各種類 の ケーキ には 3つの値 が あります。
「きれいさ xi」「おいしさ yi」「人気 zi」
3つの値 xi yi zi は 0 や マイナス の 可能性もあります。
ケーキ を 選ぶときには
(xi の 合計 の 絶対値)+(yi の 合計 の 絶対値)+(zi の 合計 の 絶対値) が
最大 になるように選びます。
選んだ M 種類 の ケーキの
(xi の 合計 の 絶対値)+(yi の 合計 の 絶対値)+(zi の 合計 の 絶対値) の
最大値 を 求めて下さい。
制約 は 下記の通りです。
N 1 以上 1000 以下。
M 0 以上 N 以下。
xi yi zi それぞれ マイナス10の11乗 以上 プラス10の11乗 以下。
【説明】
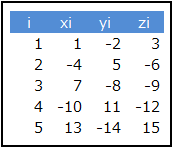
5 種類 の ケーキから 重複なしで 3 種類 の ケーキ を 選ぶ場合を考えます。
「きれいさ xi」「おいしさ yi」「人気 zi」の 3つの値 には 正と負 があります。
合計 の 絶対値 を大きくするように取得する為 3つの値 で
「正の方向 に 最大化する」「負の方向 に 最大化する」のどちらを選ぶか
2の3乗 = 8 通り について計算します。
次に それぞれを 降順ソート して 上から 3 種類 選びます。
選んだ 3種類 を合計したもののうち 最大値 が 解答 となります。
実際の問題の Accepted なソースコードは下記になります。
https://beta.atcoder.jp/contests/abc100/submissions/2964768
6. ABC 105 D Candy Distribution を解く
【問題概要】
左右一列に並んだ N 個の箱があります。
左から i 番目の箱には Ai 個の あめ が入っています。
連続した箱から あめ を取り出して M人 に均等にくばります。
左端を l 右端を r としたとき、以下の関係が成り立ちます。
1 <= l <= r <= N
Al + Al+1 + … + Ar は Mの倍数
組 (l, r) の 総数 を 求めて下さい。
制約 は 下記の通りです。
N 1 以上 10の5乗 以下
M 2 以上 10の9乗 以下
Ai 1 以上 10の9乗 以下
【説明】
13 個 の箱から選び 17人 に均等にくばる以下の場合を考えます。
10 番目の箱 ( i = 10 ) から、13 番目の箱 ( i = 13 ) まで
4 個 の箱の あめ の合計が 187 個 で 17 で 割り切れます。
これは 10 番目の箱 ( i = 10 ) の 直前 の
9 番目の箱 ( i = 9 ) までの あめ の 累積和 を 17 で 割った余り が 0 で
13 番目の箱 ( i = 13 ) までの あめ の 累積和 を 17 で 割った余り が 0 の為
17 で割りきれます。
割った余りが 0 でなくても、左端の 直前 と 右端で 割った余り が 同じ であれば良いです。
例えば 11 番目の箱 から、12 番目の箱 の あめ の 合計 51 は 17 で割り切れます。
この場合 左端の 直前 ( i = 10 ) と 右端 ( i = 12 ) で 割った余り が 4 で同じです。
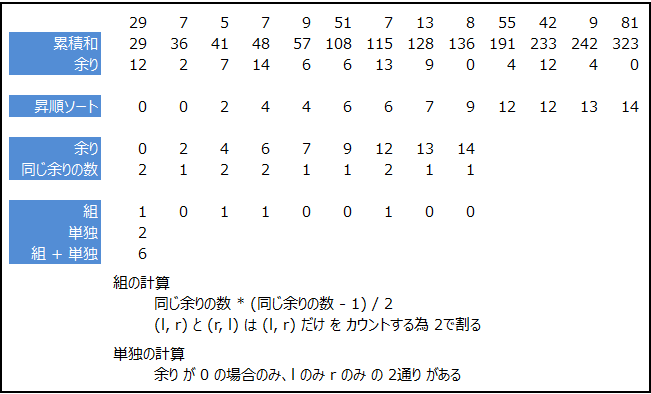
したがって、累積和 と 余り をもとめて 余りごとに 同じ余りの数 をもとめて
左端 と 右端 の 組 の数 を もとめます。
さらに 余り が ゼロ の場合だけ
一番左端から 左端の直前まで と 一番左端から 右端まで の 2 通り を
先にもとめた 数 に たしあわせる ことで解答となります。
余り と 同じ余りの数 は、C++では map などの 連想配列 が 便利 ですが
「OpenCOBOL」「opensourceCOBOL」にはありませんので 一旦 余りをソートしてから
同じ余りの数 を かぞえます。
余り については 「OpenCOBOL」「opensourceCOBOL」に MOD関数 がありますが
大きな数の MOD で 誤った数 が算出される事象を観測しました。
※具体的な値は不明ですが、以下の Wrong Answer と Accepted の ソースコード差分は
MOD をするか 自力で計算 をするか の ごくわずかの違いでした。
【Wrong Answer】
https://beta.atcoder.jp/contests/abc105/submissions/3002200
【Accepted】
https://beta.atcoder.jp/contests/abc105/submissions/3002251
自力で計算することをおすすめします。
X を M で 割った 商 を D に 余りを R に格納する下記の構文を使います。
DIVIDE M INTO X GIVING D REMAINDER R
実際の問題の Accepted なソースコードは下記になります。
https://beta.atcoder.jp/contests/abc105/submissions/3002629
当問題では 入力が 8,191 桁 以上 となる為 ACCEPTコマンド は 使用できません。
記事「AtCoder ABC 入力大き目 を COBOL で解いてみた」の内容をもとに
標準入力 を READ 文 に リダイレクトすることで 回避 しています。
https://qiita.com/ShinjiSHIBATA/items/af3c9a6a8dd26233dc7e
以上です。