朝Shorts眺めてたら流れてきた動画を一般化しようと思い、コードを作ってもらいました。
問題設定
n^nのマス目に、ランダムに点が配置されている。マス目の頂点の間は全て壁で仕切られていて、点は壁を貫通しない限り自由に動くことができる。
毎ステップ、k枚の壁が開き、各点は壁が開くことにより連結した点の集合のうちいずれかを選択する。
この時、時間に対してどれだけの点が集まれるかをプロットしたい。なお、点と点は、移動可能な「同じ空間」内にいたら即座に合流するものとし、一度合流したらその後ずっと共に移動する。
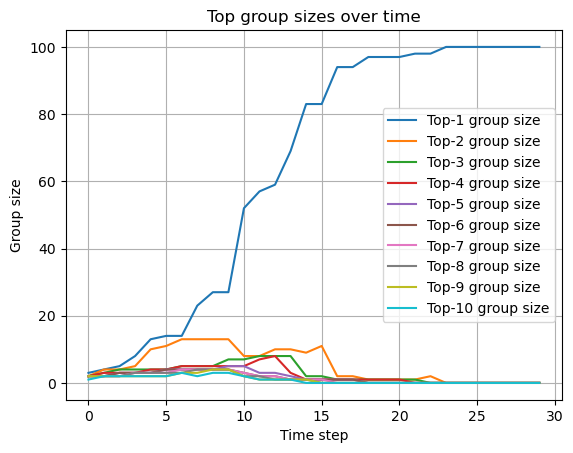
- 二次元グリッドの場合
Union Findってこういうところで使えるんだなと勉強になりました。
import numpy as np
import matplotlib.pyplot as plt
import random
from collections import defaultdict
class DSU:
def __init__(self, n):
self.parent = list(range(n))
self.size = [1]*n
def find(self, x):
while self.parent[x] != x:
self.parent[x] = self.parent[self.parent[x]]
x = self.parent[x]
return x
def union(self, x, y):
xr, yr = self.find(x), self.find(y)
if xr == yr:
return
if self.size[xr] < self.size[yr]:
xr, yr = yr, xr
self.parent[yr] = xr
self.size[xr] += self.size[yr]
def get_all_group_sizes(self):
group_sizes = defaultdict(int)
for i in range(len(self.parent)):
root = self.find(i)
group_sizes[root] += 1
return list(group_sizes.values())
def simulate_with_group_sizes(n=10, k=5, steps=100):
def index(x, y): return x * n + y
walls = []
for i in range(n):
for j in range(n-1):
walls.append(((i, j), (i, j+1)))
for j in range(n-1):
walls.append(((j, i), (j+1, i)))
dsu = DSU(n * n)
history = []
for step in range(steps):
opened = random.sample(walls, k)
for (a, b) in opened:
ax, ay = a
bx, by = b
dsu.union(index(ax, ay), index(bx, by))
history.append(sorted(dsu.get_all_group_sizes(), reverse=True))
return history
richer gets richer 的でおもろい。べきなのかなあ。
いくつかのグループがほぼ同時に集合するのもおもしろいですね.
一番目のところに吸収される(=多様性が失われる)のと、最終的によく集合することのバランスがどこでとれるかを見てみました。
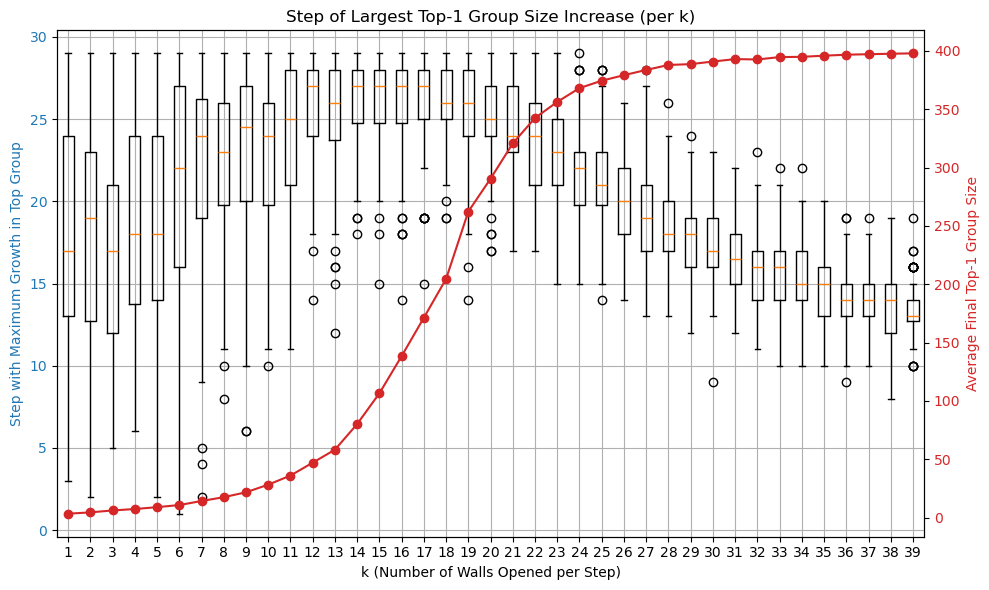
n=20で、kが横軸、各kについて100回の試行平均です。
こうしてみると、kが10%くらいのときに、状態が遷移していること、少し遅れて、より早い段階でtopの集合が早く集合することがわかります。このときだとk=15~23くらいが見ていて面白いのかもしれません。
最後に、モデルを高次元化します。
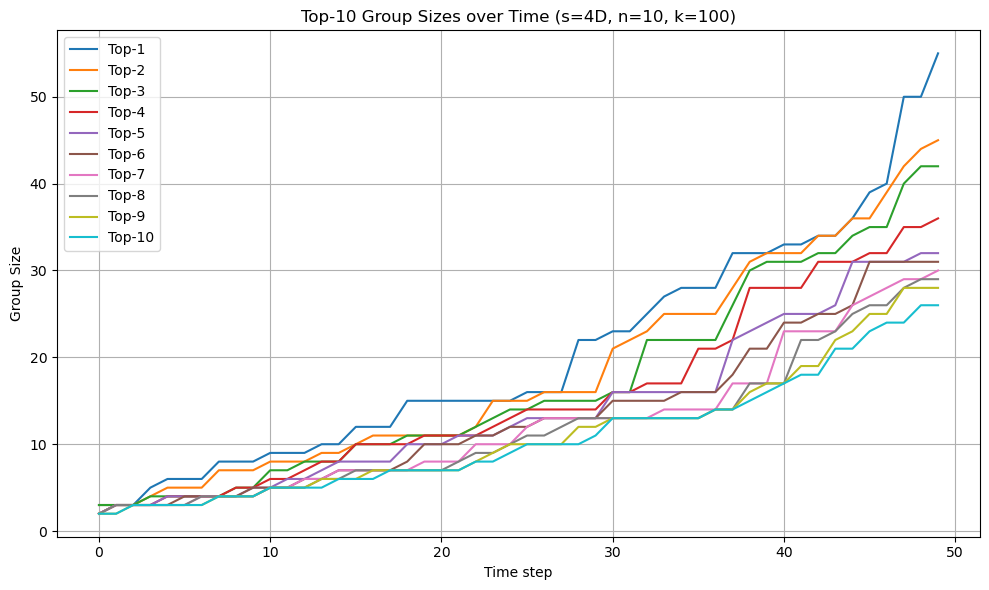
例えば4次元でn=10、つまりノードの10%が毎回解放される設定でも、このように二次元の時とは全く挙動が違います。
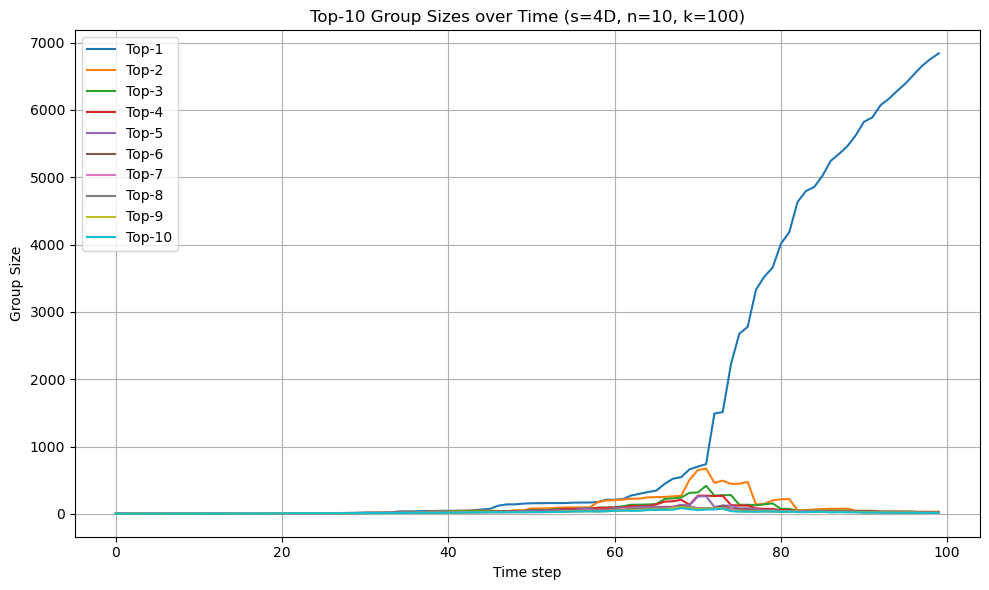
集合時間が遅くなるみたいです。これはこれで面白いですね。
ちょっと予定があるのであまり深掘りはしませんが、最後にネットワーク構造を定量的に変えてみてみようと思います。
n=1000で固定Edge(edge数はノード数の二乗の10%程度)のBAモデル上でこれをしてみましょう。
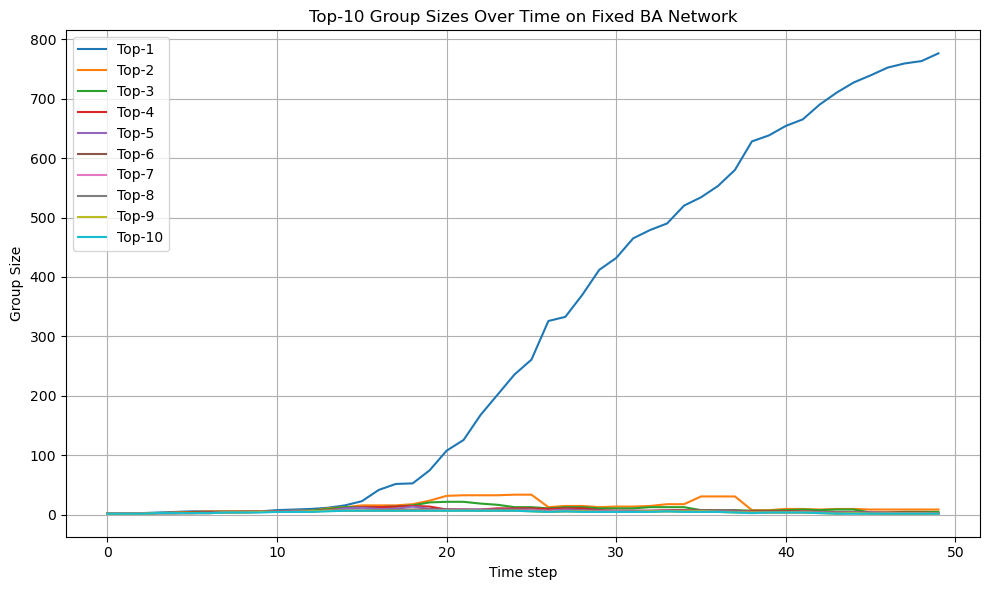
集合の様子が全く異なりました。ネットワーク指数を色々変えてもおもしろいかもしれません。
Shortsを見て思いついたのですが、かなり問題設定として面白いなと思いました。(というか、どこかにこんな問題があった気がする。)多様性とかをうまく定義できたらうれしいですね~