人間という生き物は自分で合成音声読み上げソフトを作りたい生き物です。
これは仕方のないことです。
パスカルも言ってます、人は考える葦だって。
ほらね?(は?)
まあ、とりあえずその下調べみたいなニュアンスでpythonで音を鳴らす実装を試していきます。
Chapter.0 使用言語・モジュール
- 言語:Python3系
- モジュール
- numpy(sinやπをつかうので)
- matplotlib(波形を描画したいなら)
- wave(.wavファイルの入出力に)
- struct(waveで.wavファイルにする際に波形のデータをバイナリ化するのに使います)
- pyaudio(音を鳴らすのに使いますが、Python3.7だとインストールがめんどくさいので最悪使わなくても全然大丈夫)
import numpy as np
import matplotlib.pyplot as pl
import wave
import struct
import pyaudio
Jupyter notebookならもうちょっと楽に音を鳴らせるかもしれない(詳しくは知らない)ですが、まあいいや。
Chapter1. 音を式で表現せねば…。
みなさん、音って何か知ってます?
音は周期的(?)な空気の密度の変化みたいなもんです。
要するに波です。波と言えばsin,cosですね。やった!
結論から言えば、下記のような式の正弦波を今回は使います。
sin(2πnt/s)
note_hz=n
sample_hz=s
sec = 1 #1秒
note_hz = 440 #ラの音の周波数
sample_hz = 44100 #サンプリング周波数
t = np.arange(0, sample_hz * sec) #1秒分の時間の配列を確保
wv = np.sin(2 * np.pi * note_hz * t/sample_hz)
tは1秒間の時間を表現していて、上の場合44100個の要素の1次元配列です。
私たちの住む世界の情報は連続値(アナログ)ですが、残念ながらパソコンでは離散的(デジタル)なデータしか扱えません。
なので、1秒を44100個に分割して表現するのです。
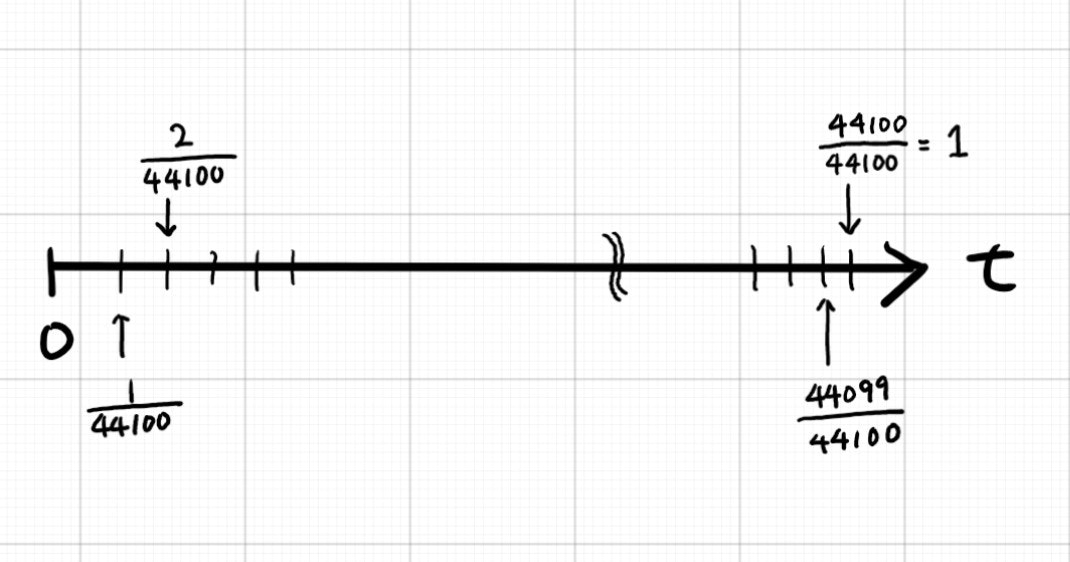
(ちなみに44100hzというサンプリング周波数は、CDのサンプリング周波数の規格で、人の可聴域の約二倍の数字にしてあります。なぜ二倍かというのはナイキスト周波数とググりましょう。)
サインの中身は2πnt/sとなっています。
t/sample_hz=t/s は、0,1,2,...,44100 と増えていく t を s=44100で割ることによって、0,1/44100,2/44100,...,44099/44100,1 と、「徐々(1/44100ずつ)に増える一秒間」を表現しています。
一旦note_hz=n を無視してnp.sin(2 * np.pi * t/sample_hz)=sin(2πt/s) を見てみると、t/s は0→1に増える変数(というよりは時間の関数?)と考えられるので、sinの中身の2πt/sは、0→2πに増えることが分かります。
つまり、sin(2πt/s)は単位円を一秒でちょうど一周する関数(一秒で一回振動する波)になります。
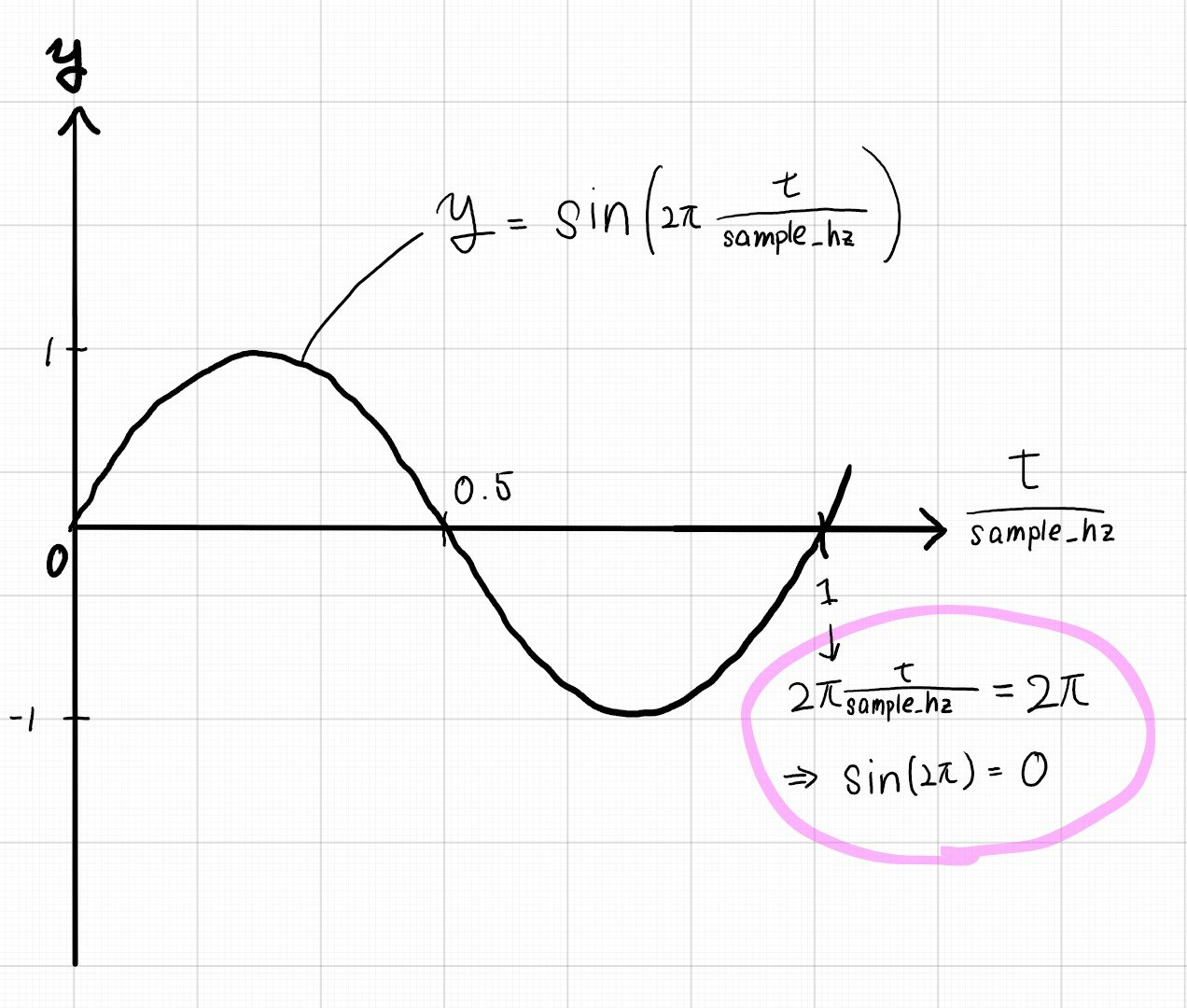
1秒で一回振動するということは、この波の周波数は1〔Hz=1/s〕です。
しかし、周波数1では音には聞こえません。
そこで登場するのが、note_hz=n です。
nを2πt/s にかけるだけで、自由自在に波の周波数を変化させることができます。
例えば、n=440とすると、*sin(2πnt/s)*は一秒間に440回振動する波(音でいえば"ラ")になります。
なんとこれでプログラム上での音の表現は完了してしまいました。
上に貼ったプログラムをもう一度コピペしておきますね。
sec = 1 #1秒
note_hz = 440 #ラの音の周波数
sample_hz = 44100 #サンプリング周波数
t = np.arange(0, sample_hz * sec) #1秒分の時間の配列を確保
wv = np.sin(2 * np.pi * note_hz * t/sample_hz)
Chapter2.プログラムで表現した音を.wavに出力しましょ。そうしましょ。
ここからの流れを説明すると、以下の通りです。
- 作った音を.wavファイルとして出力する。
- 音のデータをstructモジュールでバイナリ化する。
- バイナリ化されたデータを、waveモジュールで.wavファイルとして出力。
- 作った音をプログラム上で鳴らす。(任意)
- 作った.wavファイルをwaveモジュールで開く
- pyaudioモジュールで鳴らす。
- 音の波形をmatplotlib.pyplotモジュールでグラフとして表示する。(任意)
3.に関しては波形が気にならない人はやんなくていいです全然。
2.は、pyaudioというモジュールを使うんですが、Python3.7系だとインストールがめんどくさい(インストールしたい場合は、このページの最後の参考サイトを参照してください)ので、1.で作成した.wavファイルをWindows Media Playerなどで鳴らせばいいです。
では.wavとして出力する方法を説明していきます。
1.バイナリ化
バイナリ化です。
バイナリ化っていうのは、データを二進数にすることですね。
waveモジュールを使う際、バイナリ化しないと.wavファイルへの書き込みができないらしいです。多分。
なのでバイナリ化しましょう!
では先に答えから貼ります。
max_num = 32767.0 / max(wv) #バイナリ化の下準備の下準備
wv16 = [int(x * max_num) for x in wv] #バイナリ化の下準備
bi_wv = struct.pack("h" * len(wv16), *wv16) #バイナリ化
こんな感じです。
(というかこれ、参考にしたサイトのほぼコピペみたいなもんだけど、コピペ禁止的なマナーとかあるのだろうか…?まあいいや。)
wv=W, x=「Wの子要素のそれぞれ」= w として、[int(x * max_num) for x in wv] の中身を見ていきます。
Wのそれぞれの子要素wで、
x * max_num
=x * 32767.0 / max(wv)
= w・32767/max(W)
= 32767・(w/max(W))
と表せます。
要するに、波形データの一つ一つの値wと波形データの最大値max(W)の比をとって、32767をかけています。
32767って何の数字だよ!って思いますよね、わかります。
これは、16bitのデータ(16桁の2進数で表現されたデータ)のとりうる値が、-32768~32767であることからきています。(2の16乗が65536で、その半分の数が32768だから……うっ頭がっっっ)
w/max(W)がとりうる値は-1~1、それに32767をかけることで 32767・(w/max(W)) は -32767~32767 の値をとり、音の波形データを16bitの中にまんべんなく(というよりピッタリ?)収まるようにしています。
そうしてできるのがwv16です。ふぅ…。
そしてバイナリ化のコードbi_wv = struct.pack("h" * len(wv16), *wv16)。
正直僕はこれについて全然わかっていません。コピペです。
とりあえず、structモジュールのstruct.packはバイナリ形式への変換を行ってくれるもので、第一引数の"h"は、2byte(16bit)整数のフォーマットらしい。へぇ。
はい、バイナリ化終了!
2.waveモジュールで.wavファイルを出力
またしても先に答えを貼ります。
file = wave.open('sin_wave.wav', mode='wb') #sin_wave.wavを書き込みモードで開く。(ファイルが存在しなければ新しく作成する。)
param = (1,2,sample_hz,len(bi_wv),'NONE','not compressed') #パラメータ
file.setparams(param) #パラメータの設定
file.writeframes(bi_wv) #データの書き込み
file.close #ファイルを閉じる
こんな感じです。
wave.open()で、ファイルを開きます。
第一引数でファイルの名前を指定し、第二引数のmode=で書き込みモード('wb')か読み込みモード('rb')を設定しましょう。
wave.setparams()で.wavファイルのパラメータを設定します。
パラメータ(param)は左から順に、
- チャンネル数( ステレオ→2、モノラル→1 )
- サンプルサイズ〔byte〕(今回は2byte)
- サンプリング周波数
- フレーム数(今回でいえば
t配列の個数と同じ) - 圧縮形式(
'NONE'だけがサポートされている。それって存在意義あるんか…?) - 圧縮形式を人に判読可能にしたもの(圧縮形式
'NONE'に対して'not compressed'が返される。)
です。
そしたらバイナリ化したデータ(bi_wv)を書き込んで、ファイルを閉じます。
ファイル閉じるの忘れがちなんだよね…。
よし、できた!!
(端末やコマンドプロンプトでファイルを実行してみて、.wavファイルが生成されているか確認しましょう!)
Chapter3.めんどいからプログラム上で音鳴らしたいよな!
なので、まずwaveモジュールでさっき作ったファイルを開きます。
file = wave.open('sin_wave.wav', mode='rb')
これで開けます。
ちゃんと読み込みモードになってますね。
file = wave.open('sin_wave.wav', mode='rb')のfileという部分は変数を表してますので、別の名前でも大丈夫です。fairuとかwave_no_kiwami_otomeとか、なんでも。
まあ一応言っといただけです。
僕が初心者のころfileっていう名前じゃなきゃいけないのかな?って勘違いしてたので。
そしたらpyaudioモジュールで音を鳴らしていきます。
p = pyaudio.PyAudio() #pyaudioのインスタンス化
stream = p.open(
format = p.get_format_from_width(file.getsampwidth()),
channels = wr.getnchannels(),
rate = wr.getframerate(),
output = True
) #音を録音したり再生したりするためのストリームを作る。
file.rewind() #ポインタを先頭に戻す。
chunk = 1024 #よくわかりませんが公式ドキュメントがこうしてました。
data = file.readframes(chunk) #chunk分(1024個分)のフレーム(音の波形のデータ)を読み込む。
while data:
stream.write(data) #ストリームにデータを書き込むことで音を鳴らす。
data = file.readframes(chunk) #新しくchunk分のフレームを読み込む。
stream.close() #ストリームを閉じる。
p.terminate() #PyAudioを閉じる。
上の通り、手順は
1.pyaudioを開く、2.ストリームを開く、3.ストリームにデータを書き込んで音を鳴らす、4.ストリームを閉じる、5.pyaudioを閉じる
という感じです。
Chapter4.波形の表示
いやぁ、記事がこんなに長くなるとは。
僕もう疲れちゃったよ、パトラッシュ。
というわけでコードをバーンと貼っちゃいます。
pl.plot(t,wv)
pl.show()
なんてシンプル!
matplotlib.pyplotはいっぱい記事あるんで特に何も言いません。
終わりに
ここまで読んでくれてありがとうございます!
生涯2つ目のQiita記事にしては頑張ったぜ…。
それにしても人工音声合成ソフトは果たして自分で作れるのだろうか…。
参考サイト・文献
-
[備忘録]pythonのwaveモジュール - Qiita
- めっちゃ参考になりました。
-
pythonで音プログラミング
- Jupyter notebook を使ってるっぽいサイト。あんまり見てないです。
-
wave — Read and write WAV files
- 翻訳が微妙ですが、日本語でも読めます。
-
PyAudio Documentation
- 英語しかないっす。がんばりましょう、英語。
-
Python3.7でPyAudioがインストールできない時の解決法
- PyAudioがインストールできなくて断念しそうだったときに助けていただきました。命の恩人です。
最終的なコード
import numpy as np
import matplotlib.pyplot as pl
import wave
import struct
import pyaudio
# Chapter1
sec = 1 #1秒
note_hz = 440 #ラの音の周波数
sample_hz = 44100 #サンプリング周波数
t = np.arange(0, sample_hz * sec) #1秒分の時間の配列を確保
wv = np.sin(2 * np.pi * note_hz * t/sample_hz)
# Chapter2
max_num = 32767.0 / max(wv) #バイナリ化の下準備の下準備
wv16 = [int(x * max_num) for x in wv] #バイナリ化の下準備
bi_wv = struct.pack("h" * len(wv16), *wv16) #バイナリ化
file = wave.open('sin_wave.wav', mode='wb') #sin_wave.wavを書き込みモードで開く。(ファイルが存在しなければ新しく作成する。)
param = (1,2,sample_hz,len(bi_wv),'NONE','not compressed') #パラメータ
file.setparams(param) #パラメータの設定
file.writeframes(bi_wv) #データの書き込み
file.close #ファイルを閉じる
# Chapter3
file = wave.open('sin_wave.wav', mode='rb')
p = pyaudio.PyAudio()
stream = p.open(
format = p.get_format_from_width(file.getsampwidth()),
channels = file.getnchannels(),
rate = file.getframerate(),
output = True
)
chunk = 1024
file.rewind()
data = file.readframes(chunk)
while data:
stream.write(data)
data = file.readframes(chunk)
stream.close()
p.terminate()
# Chapter4
pl.plot(t,wv)
pl.show()