これは「文字列アルゴリズム Advent Calendar 2016」21日目の記事です。
はじめに
この記事では、文字列中に出現する回文について記述します。
回文とは、右から読んでも左から読んでも同じ、アレです。
定義
文字列 $w$ が回文であるとは、文字列 $w$ の逆文字列 $w^R$ が文字列$w$と一致することである。
以上の定義から、この記事では1文字も回文であると定義します。
回文の例
- I
文字列中の回文
文字列中に出現する回文について考えましょう。
例えば、「しましまのしまうま」という長さ9の文字列中に回文はいくつ出現するでしょうか。
1文字も回文としているので、長さ1の文字列、し、ま、し、ま、の、し、ま、う、ま、は回文です。更に、しまし、ましま、まうま、も回文です。この例には、長さ1の回文が9つ長さ3の回文が3つの計12個の出現があります。
では、長さ$n$の文字列の中に回文は最大でいくつ出現するでしょう。
答えは$\frac{1}{2}n(n+1)$個です。同一の文字のみからなる長さ$n$の文字列の例を想像すれば任意の部分文字列が回文になるので、$\frac{1}{2}n(n+1)$個出現しますね。
回文の列挙
長さ$n$の文字列には最大で$O(n^2)$個の回文が出現すると言いました。では、これらの回文全てを列挙するためにかかる時間はどれくらいでしょう。
1つ1つ調べていくと、最低でも$O(n^2)$時間はかかってしまいます。
1975年、Manacherが、$O(n)$時間で文字列中の回文を列挙するアルゴリズムを提案しました。以下、このアルゴリズムについて記述します。
※RMQや接尾辞配列、接尾辞木等を用いた$O(n)$時間のアルゴリズムも存在しますが、文字列アルゴリズムの観点から、それらを用いないManacherのアルゴリズムのみ紹介します。
極大回文
ここで回文とはどういうものかについて少し考えます。
長さ$x$の回文があるとしましょう。回文の性質より、両端を$t$文字ずつ削った長さ$x-2t$の文字列も全て回文になります。つまり、「たけやぶやけた」という回文があったとき、1文字ずつ削った「けやぶやけ」も2文字ずつ削った「やぶや」も3文字ずつ削った「ぶ」も回文になっているというわけです。
文字列中の回文に関しても同じことが言えるので、各位置を中心とする最長の回文さえ計算できれば、実質全ての回文を計算したことになります。
長さ$n$の文字列は、文字列長$n$と文字と文字の間$n-1$により、中心を$2n-1$個持ちます。よって、この$2n-1$個の中心に対してそれぞれ最長の回文を計算すれば、全て列挙したと言えます。以下、位置$i$を中心とする最長の回文を、位置$i$の極大回文と呼ぶこととします。
Manacherのアルゴリズム
文字列中の全ての極大回文を列挙します。簡単のため、長さが偶数の回文のみを列挙するアルゴリズムを記述しますが、長さが奇数のものについても同様に計算できます。記述を容易にするため、文字列$w$に出現する極大回文の集合を$MPal(w)$とし、$c$を中心とする長さ$2r$の回文を$(c,r)$とします。
アルゴリズムに必要な補題を記します。
補題
任意の$(c,r)\in MPal(w), 0 < d \leq r$に対して、(1)〜(3)のいずれかを満たす。ここで、$(c-d,r_l), (c+d,r_r) \in MPal(w)$。
(1)$r_l < r-d$ ならば $r_r = r_l$
(2)$r_l = r-d$ ならば $r_r \geq r-d$
(3)$r_l > r-d$ ならば $r_r = r-d$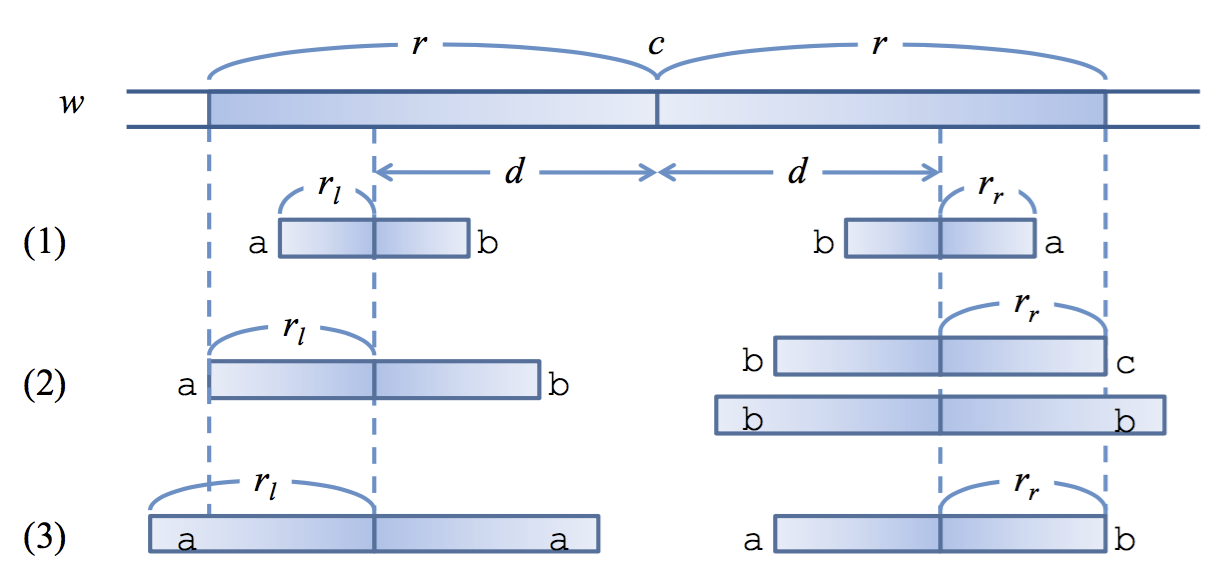
中心$c$を左から右に移動して、計算を行います。
上記の図で$c$を中心とする極大回文を計算したとし、その半径が$r$だったとしましょう。左から右に計算しているので、$c$の左側を中心とする極大回文は計算が終わっています。
補題より、$c$から$c+r$までを中心とする極大回文は、(1)〜(3)のどれかに分類できます。
(1)〜(3)に分類し、$c$の左で計算した結果をコピーし応用することで計算します。
上記の図で説明します。
$c$を中心とする極大回文を求め、長さが$2r$だったとします。
次に、$c+d$を中心とする長さ2以上の極大回文を計算していきます。
$c$の左側は計算が終わっているので、(1)もしくは(3)を満たすとき、$r_r$は$r_l$をコピーするだけで計算できます。(2)の場合、新たな極大回文の中心から左右にのばして極大回文を計算します。$r_r$を計算したら、$c$を$c+d$、$r$を$r_r$に置き換えて同じ計算を繰り返します。
$d$を1から順に大きくして計算を行い、$r$以下の全ての$d$について$c+d$を中心とする長さ2以上の極大回文がなかった場合、$c$を$c+r$に置き換えて同様の計算を行います。
以下、擬似コードです。

これにより、$O(n)$時間で極大回文を列挙できました。
おわりに
なぜ今日、回文についての記事を書いたのかについては、カレンダーを見て頂くと容易に想像がつくかと思います。
この記事は研究室の偉大な先輩方の資料を参考にさせていただきました。
拙い文章ではありますが、少しでも文字列アルゴリズム、回文について知るきっかけとなりましたら幸いです。
参考文献
- Glenn K. Manacher:
A New Linear-Time ``On-Line'' Algorithm for Finding the Smallest Initial Palindrome of a String. J. ACM 22(3): 346-351 (1975)