プリム法とは
最小全域木を構成するためのアルゴリズム
以下のようなアルゴリズムで表されます。
def prim(G(V,E))
任意の始点を選び全域木の部分木(以下T)に加える
while 全域木が構成されていない間
TとV-Tを繋ぐ辺の中でコスト最小の辺を選びTに加える
非常に素直なアルゴリズムですね。。
実装的には
・Tに加えたらTに入ってるかどうかを表すフラグをTrueにする
・TとV-Tを繋ぐ辺全てを見てコスト最小のものを選ぶのは大変なので、Tに新しく頂点が加わったときにその頂点とV-Tを結ぶ辺のうちコストがより小さくなるのであれば最小コストを更新する
とかが考えられますね。
プリム法の正しさの証明
とても素直なアルゴリズムなので本当に最小全域木が得られるのか疑問に思うかもしれませんが、以下に示すように背理法で正しさを証明できます。
仮にプリム法によって得られた全域木が最小コスト和でないと仮定する。
そのとき図のようにプリム法で選んだ辺 eよりもコストの小さい辺 e'を含むような最小全域木が存在する。
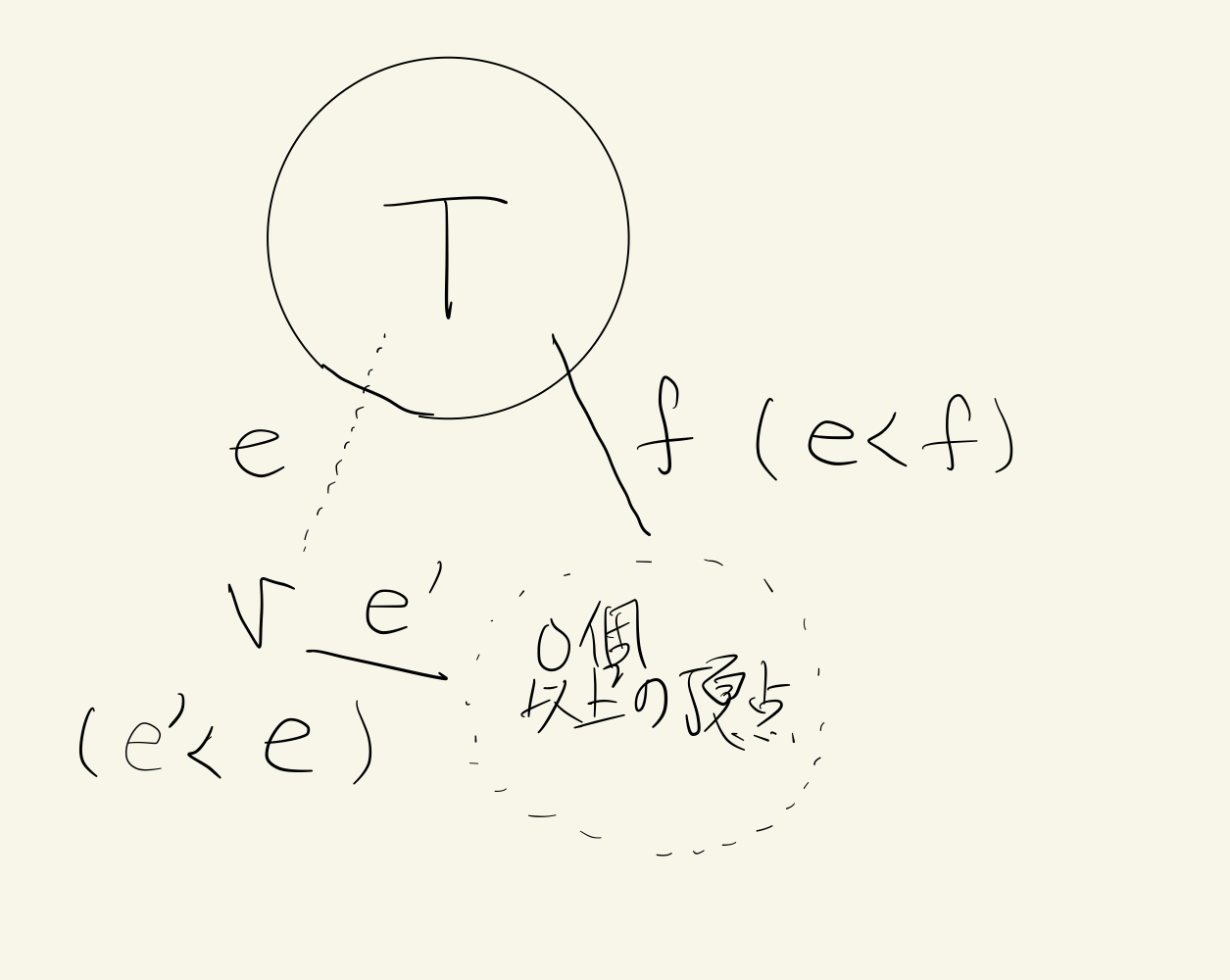
ここでプリム法でfではなくeが選ばれたことからe < fということもわかる。
この図からわかるように明らかにfではなくeを含んだ場合でも全域性は担保されており、コスト和は小さくなる。
このことから図の場合は必ず最小全域木ではないことがわかり、プリム法によって得られた全域木が最小コストでないという仮定が誤りであることがわかる。
このことからプリム法によって全域木の部分木とそれ以外とを繋ぐ辺のうちコスト最小の辺を選ぶことによって必ず最小全域木が得られることが示された。