最大長方形アルゴリズム

問題設定

AOJ-最大長方形
一辺1cmのタイルが$H\times W$並んでいる。（以下テーブルとする）
タイルは汚れているものときれいなものがあり
このうち綺麗なもののみを選んでできる最大の長方形の面積を求める。

素朴な解法

$H\times W$の全てのタイルを始点として、可能な全ての幅の長方形を考え,その中でタイルが汚れているものがあるかどうかを調べる。
始点の総数は$O(H\times W)$
ある始点に対する長方形のパターンは$O(H\times W)$
その長方形内部の調べるべき点の総数は$O(H\times W)$
以上より全体のオーダーは$O((H\times W)^3 )$

改良した解法

長方形の全ての高さについて、その高さの位置を下辺とした長方形を列挙しても十分。
ある高さを下辺とした長方形のうちの最大面積を記録し、全ての高さの最大面積のうち、最大のものを出力すれば良い。
ある高さを下辺とした長方形の最大面積を求めるために
テーブルの各要素について上に向かって何枚綺麗なタイルが続いているかを記録し
ヒストグラムを構成した上で、そのヒストグラムの最大長方形を求める。

ヒストグラムの最大長方形

素朴なアルゴリズムとしては
各要素の組み合わせに対して、それを端点とするような長方形を考え、最大の面積を求める方法が考えられるが
要素数を$n$とすると$O(n^2)$となる。
これを改善し$O(n$)とするために以下のような方法基づき最大面積を求める。
図に示すようなヒストグラムを考える。

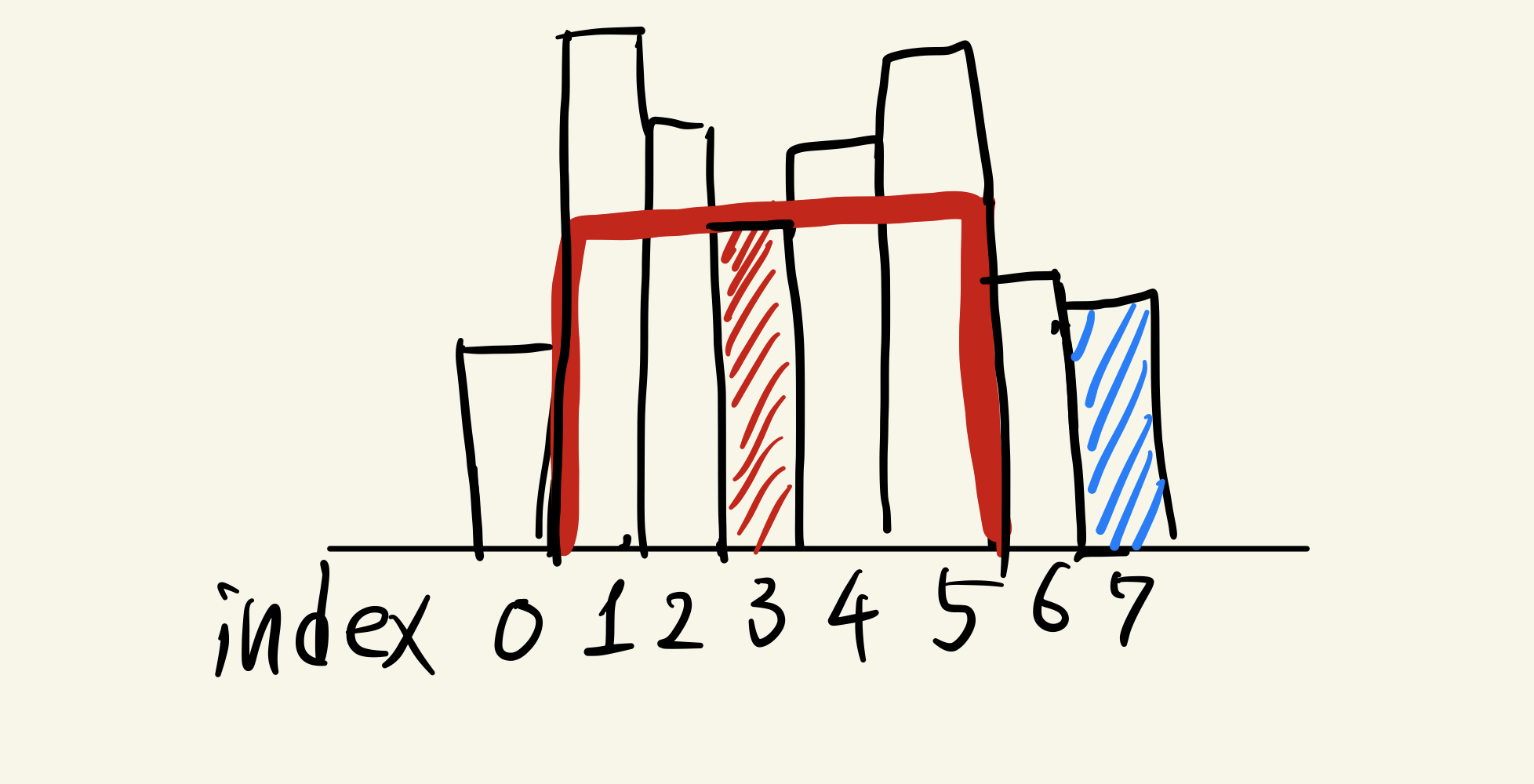
あるindexの要素を高さとするような長方形の面積は以下の式で求まる。

面積 = 自分の高さ $\times (rightIdx - leftIdx + 1)$
ただし
$rightIdx$ = 自分より右側で初めて自分より高さが小さくなる要素のindex - 1
$leftIdx$ = 自分より左側で初めて自分より高さが小さくなる要素のindex + 1
上の図の場合には $rightIdx$ = 5, $leftIdx$ = 1 となる。
この面積をヒストグラムの各要素について求めていき、最大値をとることで目的の面積が求まる。
この面積を求める流れを以下の規則に基づいて行うことで$O(n)$とすることができる。

規則: 左から順に何らかのデータ構造に要素を入れていき、自分の高さが前までの要素より小さければ自分の高さより大きいもの全てを取り出す

この規則は以下の点がポイントになる
①自分より大きいものを全てを取り出すことで、データ構造は必ず昇順になっている
②昇順のデータ構造から自分より大きいものを全て取り出すことで、最後に取り出した要素のindexが$leftIdx$となっている
③自分が取り出されたとき、挿入された要素のindex-1が$rightIdx$になっている
このように上のような規則を定義したことによって各要素の挿入、取り出しという一連の流れで
必ず$leftIdx$および$rightIdx$が求まり、面積が求まることがわかる。
また、データ構造は必ず昇順になり、なおかつ高さが高いものから取り出せば良いのでスタックが適していることがわかる。
さらに上記で述べた「取り出し」操作は不可逆であり、取り出したのちにデータ構造に戻されることはない。
このことからヒストグラム全体で挿入される回数、取り出される回数は$O(n)$であり
ヒストグラム内の全ての長方形の面積が$O(n)$で求まることがわかる。

leftIdxを求めるときの注意点

②昇順のデータ構造から自分より大きいものを全て取り出すことで、最後に取り出した要素のindexが$leftIdx$となっている

と示したが,図で青で示した要素の$leftIdx$は1となるべきだが、index1 ~ 5の要素は青で示した要素を挿入する以前にスタックから取り出されているはずである。
そのため、実装する上では$leftIdx$は最後に取り出した要素の$leftIdx$とするべきである。
なぜなら取り出した要素の$leftIdx$は取り出した要素より値が大きい範囲の下限を示しており、
青の要素は取り出した要素（index6）よりも小さいため、取り出した要素の$leftIdx$ ~ 取り出した要素が青の要素より小さいことは保証される。
そのため、少なくともindex6の$leftIdx$までは青の要素の$leftIdx$になりうる。
それより左側については,もし存在するならばスタックに入っているので、さらに大小比較を行い、青の要素の方が小さければさらに左まで辿っていき、青の要素の方が大きければそこで打ち切れば良い。

実装

最後にC++で実装したコードを示す。

#include <bits/stdc++.h>
using namespace std;
struct Rect
{
  int rightIdx;
  int leftIdx;
  int height;
};
int maxHistogramRect(vector<int> &histogram)
{
  int maxArea = 0;
  int histogramSize = histogram.size();
  stack<Rect> weightStack;
  for (int i = 0; i < histogramSize; i++)
  {
    Rect newRect;
    newRect.height = histogram[i];
    //空なのは最初だけ、それ以降は空でないことが保証できる
    if (weightStack.empty())
    {
      newRect.leftIdx = i;
      weightStack.push(newRect);
      maxArea = 1 * newRect.height;
    }
    //取り出されたものは戻されることはなく、一方通行だからO(n)
    else
    {
      int lastLeftIdx = i;
      while (!weightStack.empty() && weightStack.top().height > histogram[i])
      {
        weightStack.top().rightIdx = i - 1;
        int area = (weightStack.top().rightIdx - weightStack.top().leftIdx + 1) * weightStack.top().height;
        if (maxArea < area)
          maxArea = area;
        lastLeftIdx = weightStack.top().leftIdx;
        weightStack.pop();
      }
      Rect newRect;
      newRect.height = histogram[i];
      newRect.leftIdx = lastLeftIdx;
      weightStack.push(newRect);
    }
  }
  //weightStackに残ったものについての面積を計算する
  while (!weightStack.empty())
  {
    weightStack.top().rightIdx = histogramSize - 1;
    int area = (weightStack.top().rightIdx - weightStack.top().leftIdx + 1) * weightStack.top().height;
    if (maxArea < area)
      maxArea = area;
    weightStack.pop();
  }
  return maxArea;
}
int main()
{
  cin.tie(0);
  ios::sync_with_stdio(false);
  int h, w;
  cin >> h >> w;
  vector<int> table = vector<int>(w, 0);
  int overallMaxArea = 0;
  for (int i = 0; i < h; ++i)
  {
    for (int j = 0; j < w; ++j)
    {
      int available;
      cin >> available;
      if (available == 1)
      {
        table[j] = 0;
      }
      else
      {
        table[j] = table[j] + 1;
      }
    }
    int maxArea = maxHistogramRect(table);
    if (overallMaxArea < maxArea)
      overallMaxArea = maxArea;
  }
  cout << overallMaxArea << endl;
}