はじめに
非線形な連続時間確率過程を数値計算する方法として、
近接再起アルゴリズムというのが提唱された。
https://arxiv.org/abs/1908.00533
詳細な数学のお話は論文を参照してください（気が向いたら書くかも）。
どういうアルゴリズムか
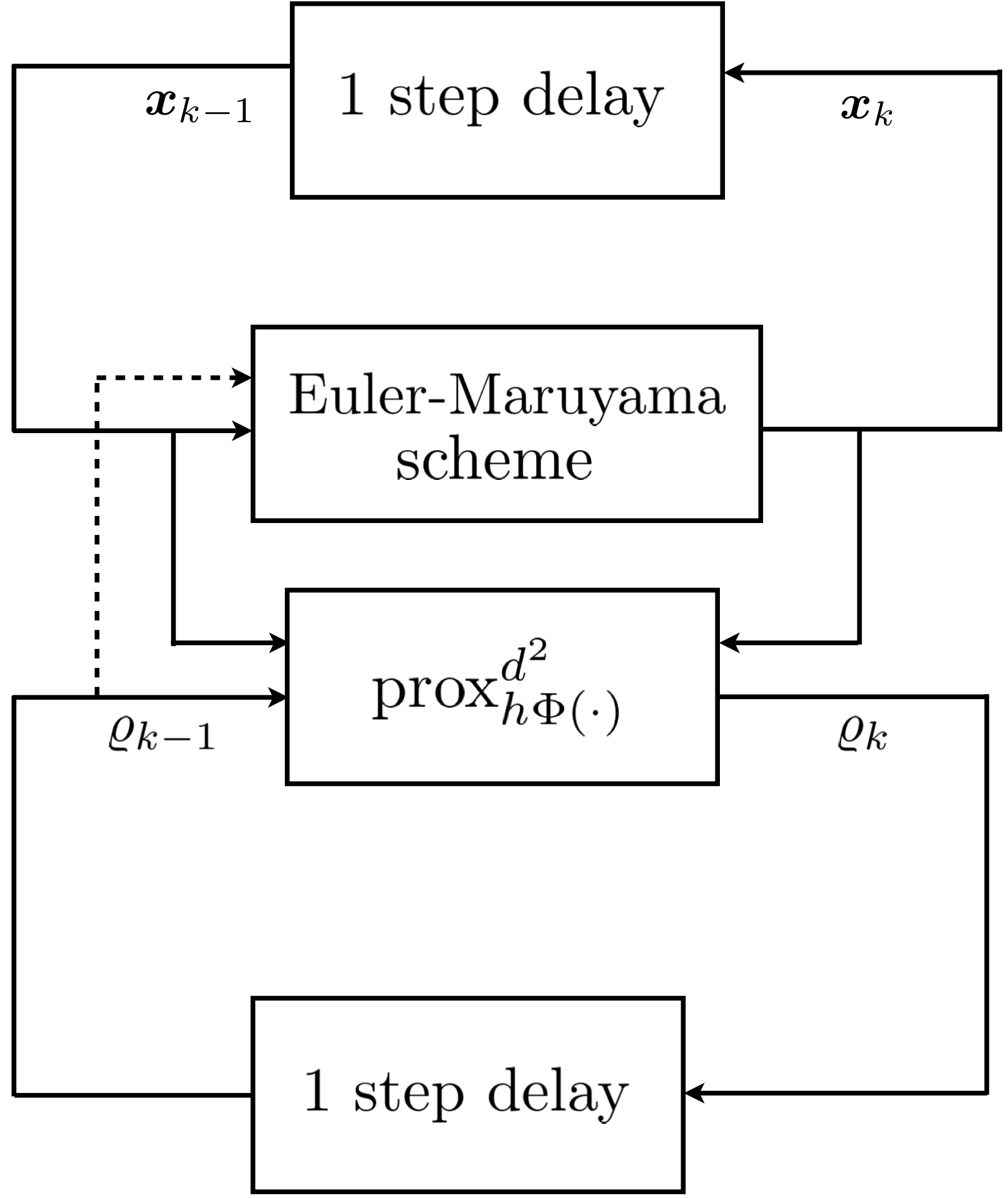
Euler-Maruyamaスキームなどで$N$個の粒子の位置$\displaystyle{\boldsymbol{x}}_k$を計算し、
その分布から$t$における粒子分布$\displaystyle\varrho_{k}(\boldsymbol{x}_k)$を推定する。
（引用：https://arxiv.org/pdf/1908.00533.pdf）
まず$\displaystyle\boldsymbol{x}_{k}$を求める。
$\displaystyle\boldsymbol{x}_k$ と1ステップ前の分布$\varrho_{k-1}$から$\varrho_{k}$を求める。
そして次のステップに進む、というアルゴリズムである。
モデル
伊藤型の確率微分方程式を考える。
\displaystyle d\boldsymbol{x} = - \nabla\psi(\boldsymbol{x})dt + \sqrt{2\beta^{-1}} d\boldsymbol{w}
ここで$\psi: \mathbb{R}^n \mapsto (0,\infty)$は移流ポテンシャル、$\beta$ は拡散係数である。
これをFokker-Planck 方程式にすると次式となる。
\cfrac{\partial\rho}{\partial t}
= \nabla \cdot (\rho \nabla\psi)+ \beta^{-1} \Delta\rho
$\Delta$ はラプラシアンを表す。
また、アルゴリズムに用いるため行列$\displaystyle\boldsymbol{C}_k$を次式で導入する。
\boldsymbol{C}_k (i,j) =
\parallel \boldsymbol{x}^i_k - \boldsymbol{x}^j_{k-1} \parallel_2^2,
\quad
(i,j=1,\dots,N)
$(i,j)$成分が$k$ ステップ目の粒子$i$と$k-1$ステップ目の粒子$j$の距離の2乗となるように決める。
Proximalアルゴリズム
（引用：https://arxiv.org/pdf/1908.00533.pdf）
引数はそれぞれ
- $\boldsymbol{\varrho}_{k-1}$: 前ステップの分布。
- $\boldsymbol{\psi}_k$: $k$ ステップでの各粒子のポテンシャル。
- $\boldsymbol{C}_k$: 先ほど導入した距離の二乗の行列。
- $\beta$: 拡散係数。
- $h$: ステップサイズ。
- $\epsilon$: 正則化定数。
- $N$: 粒子数。
- $\delta$: 許容誤差。
- $L$: 最大繰り返し回数。
Pythonでの実装
import numpy as np
from numpy import random as rand
from numpy.linalg import norm
def proxRecur (sigma, psi, C, delta=0.001, L=100):
Gamma = np.exp (-0.5*C/epsilon)
xi = np.exp (-beta*psi - 1)
z = np.zeros ((N, L))
y = np.zeros ((N, L))
z[:,0] = rand.uniform (size=(N,))
y[:,0] = sigma / (Gamma @ z[:,0])
for l in range (L-1):
z[:,l+1] = np.power (xi / (Gamma.T @ y[:,l]), 1.0/(1+beta*epsilon/h))
y[:,l+1] = sigma / (Gamma @ z[:,l+1])
if norm(z[:,l+1]-z[:,l])<delta and norm(y[:,l+1]-y[:,l])<delta:
return z[:,l+1] * (Gamma.T @ y[:,l+1])
return z[:,L-1] * (Gamma.T @ y[:,L-1])
論文中のアルゴリズムで出てくる引数のうちいくつか（例えば拡散係数$\beta$など）はEuler-Maruyamaスキームなどで確率微分方程式を直接解くときにも用いるため、大域変数として扱っている。
Ornstein-Uhlenbeck 過程
簡単な確率微分方程式の例として、1次元のOrnstein-Uhlenbeck 過程を考える。
初期の粒子の分布は$\mathcal{N}(\mu_0, \sigma_0^2)$とする。
\begin{align}
dx = -a x dt + \sqrt{2\beta^{-1}} dW
\end{align}
これのEuler-Maruyamaスキームと近接再起アルゴリズムの実装は次のようになる。
def eulerMaruyama (initStates, initDistbs):
maxIter = 4000
states = np.zeros ((N, maxIter+1))
distbs = np.zeros ((N, maxIter+1))
order = np.argsort (initStates.reshape((N,)))
states[:,0] = (initStates.reshape ((N,)))[order]
distbs[:,0] = (initDistbs.reshape ((N,)))[order]
for idx in range (maxIter):
dstates = - a * states[:,idx] * h + np.sqrt(2*h/beta) * rand.normal (size=(N,))
tmp = states[:,idx] + dstates
states[:,idx+1] = np.sort (tmp)
psi = a * states[:,idx+1]*states[:,idx+1] / 2.0
C = (states[:,idx+1].reshape((N,1)) - states[:,idx].reshape((1,N))) ** 2
distbs[:,idx+1] = proxRecur (distbs[:,idx], psi, C)
# Integration
dx = np.diff (states[:,idx+1])
Z = (distbs[:-1,idx+1] + distbs[1:,idx+1])/2 @ dx
distbs[:,idx+1] /= Z
return states, distbs
論文中には明示されていないが、近接再起アルゴリズムでは分布が正規化されない。
そのため粒子の座標でソートを行い、proxRecur関数で分布を求めた後に積分を行って正規化をしている。
数値積分は台形則に基づいて行っている。
最後に状態と各粒子の分布の値のペアを返している。
数値計算結果
論文中では
\begin{align}
a=1, \quad
\beta=1, \quad
h = 10^{-3}, \quad
\epsilon = 0.05, \quad
N = 400, \quad
\mu_0 = 5.0, \quad
\sigma_0^2 = 0.04
\end{align}
で数値計算を行っている。
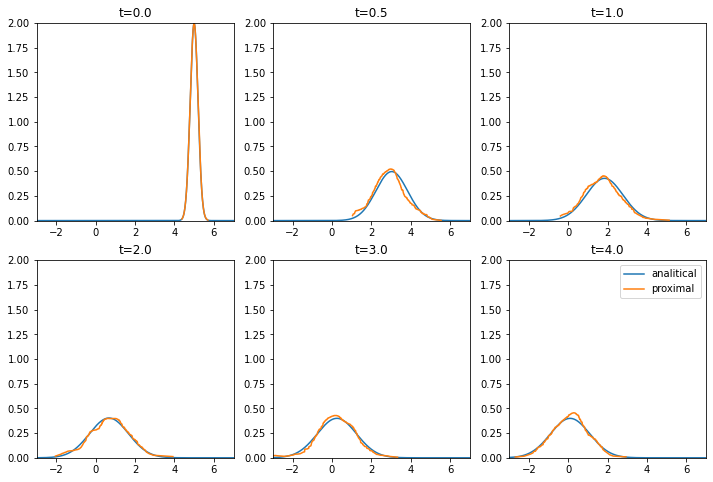
私も同じパラメータで数値計算を行ってみた。
上図は各時刻ごとの解析解（水色線）と近接再起アルゴリズムでの解（橙線）の比較である。
定性的な振る舞いは一致している。
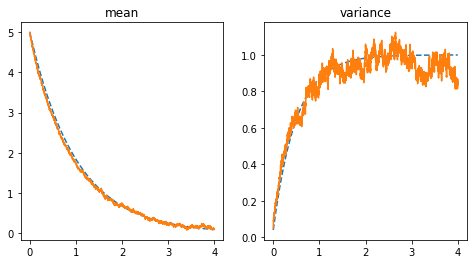
上図は平均（左図）と分散（右図）の時間変化である。
破線が解析解、橙実線が近接再起アルゴリズムでの解となっている。
平均はほぼ一致しており、分散も解析解を中心に揺らいでいるため、良い結果が得られているものと考えられる。
まとめ
非線形な連続時間確率過程を数値計算する方法として近接再起アルゴリズムというのが提唱されたので、これをpythonで実装してみた。
簡単な1次元のOrnstein-Uhlenbeck過程でシミュレーションをしたところ、かなり良い性能が得られた。
参考文献
Kenneth F. Caluya, and Abhishek Halder, ``Gradient Flow Algorithms for Density Propagation in Stochastic Systems'', arXiv:1908.00533