MIDIで12平均律以外の音律を使ってみる

0. まずは

こんにちは。プログラミングの内容はほぼありません、雑記です。

私たちは普段1オクターブを12個に(対数的に)等分した12平均律を使っています。実際、インターネット上に存在する99.9%以上の曲は12平均律でしょう。では、1オクターブを12以外の数で等分してみるとどうなるでしょう？
これらの音楽は Xenharmonic Music などと呼ばれます(平均律以外も含む)。
例えば、5平均律、7平均律、31平均律なんかがメジャーですね。あとは平均律以外で言うとピタゴラス音律、純正律などもよく使われていました(音の数は12個)。
そして、今回はそのゼンなんちゃらで曲を作ってみよう、という話です。

通常の楽器やDAW(作曲ソフト)は12平均律に調律されており、鍵盤も12個しかありません。しかしながら昨今は便利な世の中です、12平均律以外の音を出せるプラグインやVSTは探せばたくさん見つかります。
...ただ私はめんどくさがりなので、MIDIの調律機能を用いて特殊な音律を再現していきます。

1. どうするか

結論から言うと、MIDI Tuning Standard (MTS) というMIDIの機能を使います。
MTSはMIDIの128音それぞれ、もしくはオクターブ12音ごとに音の周波数を決めることができ、これで調律します。

また、MIDIを編集するソフトとして、Domino を使用させていただきます。

MIDIを編集できるDAWなどでも同様のことができると思います。

2. MIDI Tuning Standard

MTSはシステムエクスクルーシブメッセージというメッセージイベントの記述方法の1つです。
エクスクルーシブメッセージは通常メーカーごとに異なりますが、MTSは全ての規格で共通です。ユニバーサルエクスクルーシブという面白い名前になってますね。

メッセージの種類はいろいろあるのですがここではMTSのうち1つだけ解説します。他は上記のpdfに載ってるので気になれば見てみてください。

MTSにはリアルタイムと非リアルタイムのものがあり、

• リアルタイム ... 鳴っている最中の音にも変更を適用する。
• 非リアルタイム ... 鳴っている最中の音には変更を適用しない セットアップ用。

という違いがあります。今回は曲の最初に1度だけ使うので非リアルタイムでOKですが、書き方はほぼ同じです。

また、単音のみ変更、すべての音をそれぞれ変更、オクターブごとに変更の3種類あり、通常はオクターブごとに変更で事足ります。解説するのはこれ。

画像の通り、以下の構文で記述します。

F0 7E <device ID> 08 09 ff gg hh [ss tt]*12 F7

• F0 7E ... ユニバーサルシステムエクスクルーシブ、非リアルタイム
• <device ID> ... 変更するデバイス(7FでOK)
• 08 ... MTS
• 09 ... オクターブごとに変更、2バイトずつ
• ff gg hh ... 変更するチャンネル
• [ss tt]*12 ... 基準音(C, C#, D...)からのズレ
• F7 ... エクスクルーシブメッセージの終わり

基本的に16進数ですがそこまで難しくないので安心してください。

ff gg hh

これらを2進数にすると
00000000 00000000 00000000
で、24個の0のうち、バイト(8個のかたまり)の左端を無視して 変更するチャンネルを右から1にします。
例えば、チャンネル 2, 3, 5, 7, 11, 13 を変更したいとき、
00000000 00101000 01010110 となります。
全て変更する場合は 00000011 01111111 01111111 です。

そして... これを16進数に直せば完成です。

• 00000000 00101000 01010110 → 00 28 56
• 00000011 01111111 01111111 → 03 7F 7F

[ss tt]*12

これは基準音からの音のズレをCから順に12回指定します。
これも2進数にすると
00000000 00000000 となり、例によってバイトの左端は無視します。

• 00000000 00000000 ... -100¢、半音下
• 01000000 00000000 ... 変更なし
• 01111111 01111111 ... +100¢、半音上

のように、基準音から上下2半音を16384個に分割して指定します。
半音の1/8192の精度、0.0122¢単位で調整できるので、到底人間の耳では判別できません。¢単位でしか調整できないプラグインもあるのを考えるとこれは嬉しいですね。

(¢, cent ... 半音の1/100の単位)

12平均律j番目の音 と a平均律i番目の音 の周波数比をズレnに変換すると

n=\log_{\left(\sqrt[12\cdot2^{13}]{2}\right)}\left(\frac{\sqrt[a]{2}^{i}}{\sqrt[12]{2}^{j}}\right)+8192=8192\left(\frac{12i}{a}-j+1\right)

あとはこれを整数に丸めて14ビットの2進数に変換し、7ビットごとに0を入れ16進数に直せば完成です。

• 12平均律2番目の音 と 7平均律1番目の音 の周波数比 = 0.984 = -28.6¢
  5851 ₁₀ → 01011011011011 ₂ → 00101101 01011011 ₂ → 2D 5B ₁₆
• 12平均律7番目の音 と 10平均律6番目の音 の周波数比 = 1.01 = +20.0¢
  9830 ₁₀ → 10011001100110 ₂ → 01001100 01100110 ₂ → 4C 66 ₁₆

また、a平均律i番目の音 に最も近い 12平均律j番目の音 は

j=\log_{\left(\sqrt[12]{2}\right)}\left(\sqrt[a]{2}^{i}\right)=\frac{12i}{a}

を整数に丸めたものです。
平均律で説明しましたが、純正律など、12以下の音律であれば同様に作れます。

音を指定する順番は C, C#, D, ..., B なので、Cが基準となりますが、順番を入れ替えばもちろん他の音を基準にすることも可能です。

3. メッセージの送信

上記の内容をもとに、C基準で7平均律のセットアップを作ると、

message: F0 7E 7F 08 09 03 7F 7F 40 00 40 00 2D 5B 5B 37 40 00 49 12 40 00 36 6E 40 00 24 49 52 25 40 00 F7
keys: C, D, D#, F, G, A, A#

こうなります。
ソフト上でエクスクルーシブイベントを挿入し、messageを入力すれば7平均律のセットアップ完了です。なお、挿入するトラックはどこでもいいですが、リセットイベントの前に挿入するとリセットされてしまいます。

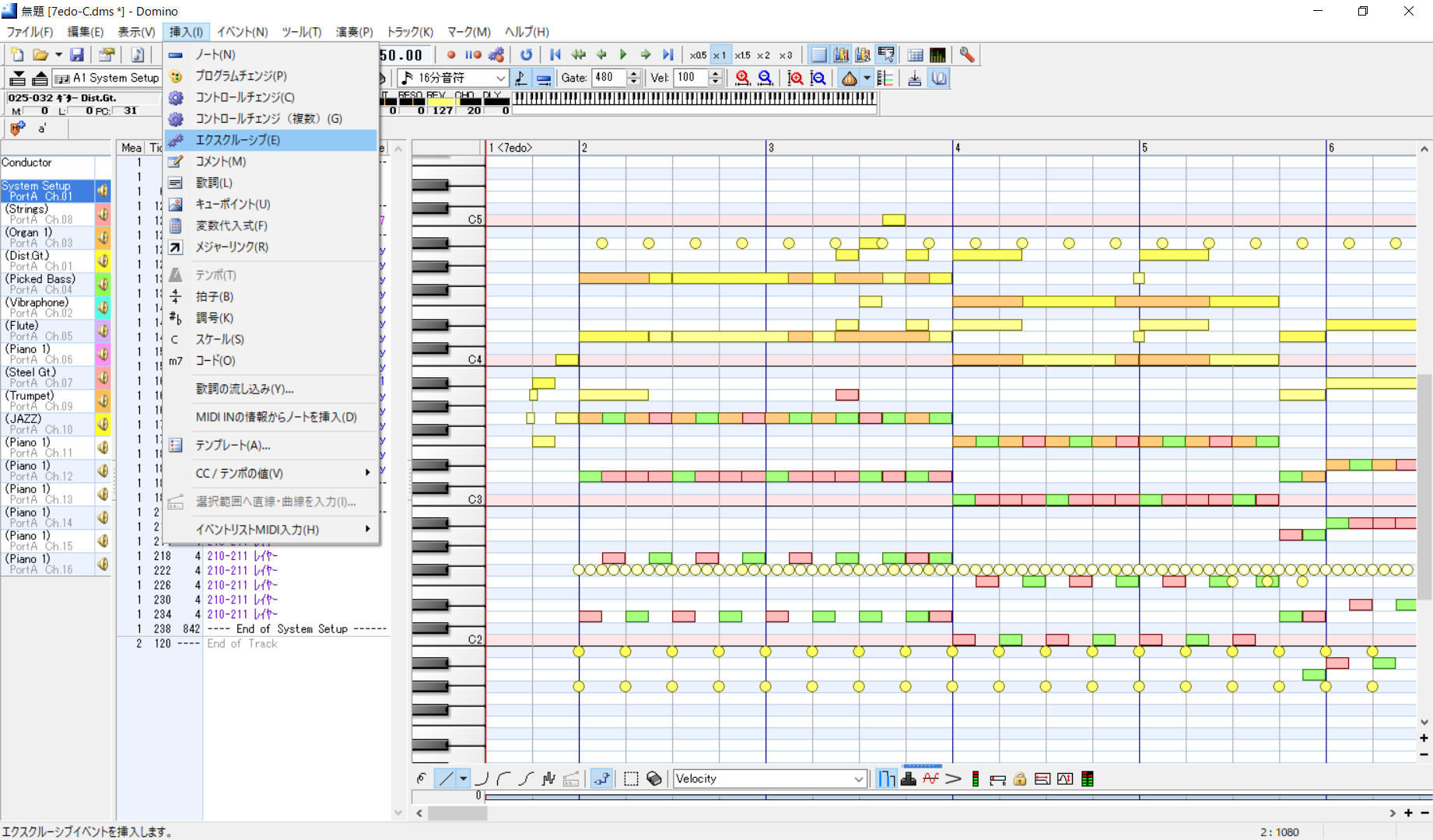
(Dominoでは16進数の前に0x もしくは後にhを付ける必要があります。)

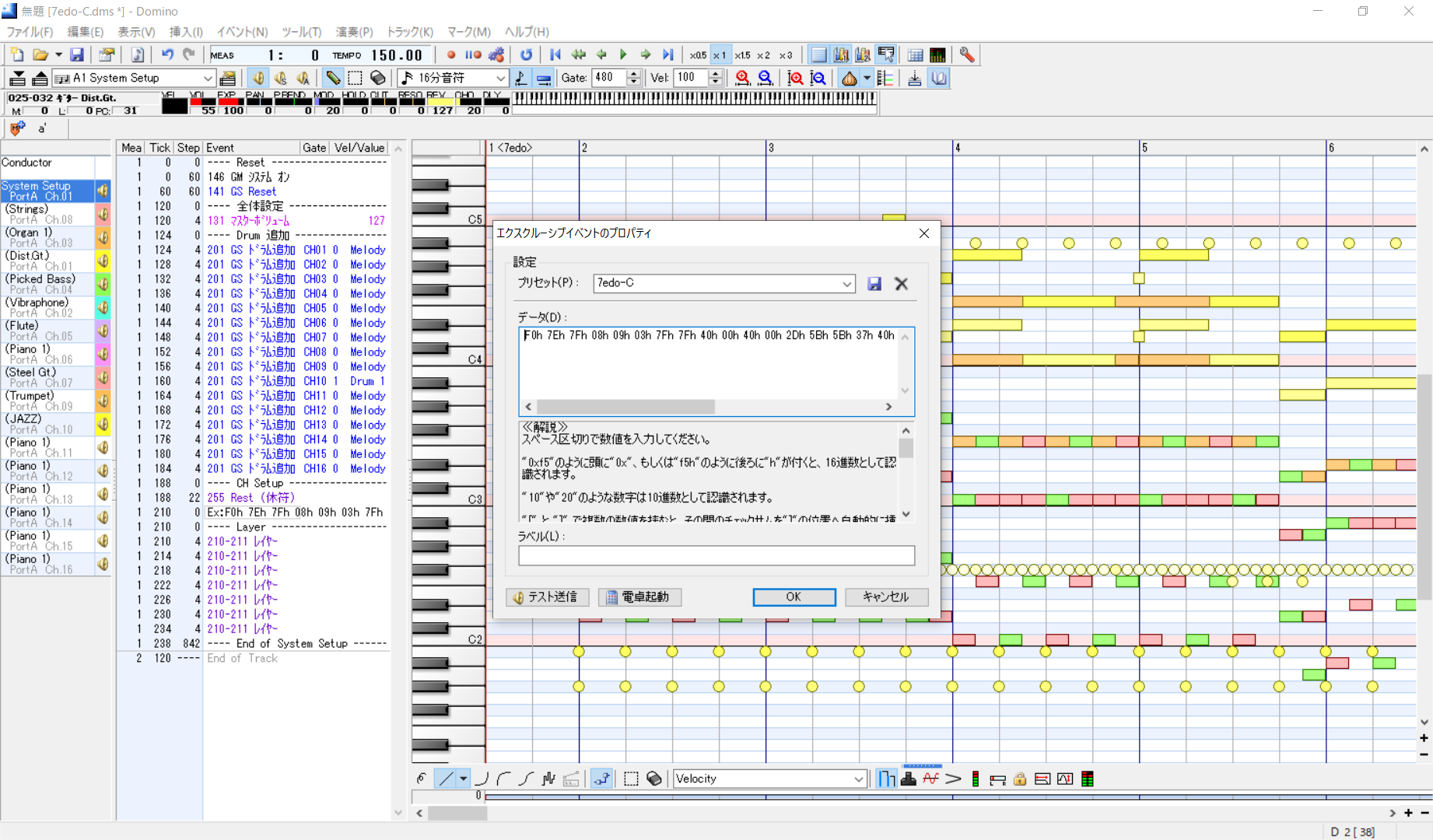
使うキーに背景色をつけるなどしてわかりやすくしてください。
使わなかったキーは元の音のままなのでご注意を。

5. 12より大きい音律

12以下であればオクターブ内の音の音程を変えるだけでいいですが、12より大きくなると足りなくなります。そこでよく使われる手法が、複数トラックを用意する です。

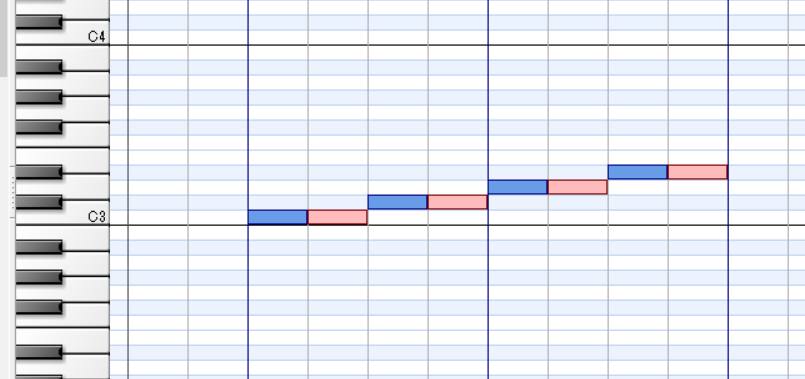
画像は24平均律で、青いノートが通常の12平均律の音、赤いノートがそれより半半音(50¢)高い音で、2つのトラックを使用しています。ピッチの上げ下げは Pitch Bend を使うとよいでしょう、MTSと同じ精度で変えられます。

こればっかりはしょうがないというか、ソフトを根本から新しい仕様で作らないとけないので苦肉の策とも言えますね...。
DAWによってはノートのトラック間移動をショートカットに割り当てられるので、やりやすいものを選ぶといいと思います。本末転倒。

ただ、1つの調内で使われるキーの数は7つ程度ですので、12より大きい音律であっても使うキーのみ選んで12個に収めれば問題なく打ち込めます(私はこの方法でやっています)。転調のたびにエクスクルーシブイベントを挿入すれば転調もOK。

4. プログラム

edo平均律、基準baseNoteでのセットアップ。12以下用。

JavaScript

const edo = 7;
const baseNote = "A";

let keyNames = ["C", "C#", "D", "D#", "E", "F", "F#", "G", "G#", "A", "A#", "B"];
let message = "F0h 7Eh 7Fh 08h 09h 03h 7Fh 7Fh ";
const selectedKeyNames = [];
let bytes = [];

const baseIndex = keyNames.indexOf(baseNote);

function turnArray(array, num) {
  return array.slice(num).concat(array.slice(0, num));
}

keyNames = turnArray(keyNames, baseIndex);

for (let i = 0; i < 12; i ++) {
  bytes.push("40h 00h ");
}

for (let i = 0; i < edo; i ++) {
  const key = 12 * i / edo;
  const index = Math.round(key);
  const rate = Math.round(8192 * (key - index + 1));

  const bin14 = rate.toString(2).padStart(14, "0");
  const bin16 = `0${bin14.slice(0, 7)}0${bin14.slice(7)}`;
  const hex = parseInt(bin16, 2).toString(16).toUpperCase().padStart(4, "0");

  bytes[index] = `${hex.slice(0, 2)}h ${hex.slice(2)}h `;
  selectedKeyNames.push(keyNames[index]);
}

bytes = turnArray(bytes, 12 - baseIndex);
message += `${bytes.join("")}F7h`;

console.log(message);
console.log(selectedKeyNames);

edo平均律の1音をdivision分割したときのPitch Bendの変化量。

JavaScript

const edo = 7;
const division = 2;

const pitch = Math.round(49152 / (edo * division));
console.log(pitch);

純正律、基準baseNoteでのセットアップ。
ratiosを変えればピタゴラス音律、中全音律などにも。

JavaScript

const baseNote = "C";

let keyNames = ["C", "C#", "D", "D#", "E", "F", "F#", "G", "G#", "A", "A#", "B"];
const ratios = [1, 16/15, 9/8, 6/5, 5/4, 4/3, 45/32, 3/2, 8/5, 5/3, 9/5, 15/8];
let message = "F0h 7Eh 7Fh 08h 09h 03h 7Fh 7Fh ";
let bytes = [];

const baseIndex = keyNames.indexOf(baseNote);

function turnArray(array, num) {
  return array.slice(num).concat(array.slice(0, num));
}

keyNames = turnArray(keyNames, baseIndex);

for (let i = 0; i < 12; i ++) {
  const rate = Math.round(8192 * (12 * Math.log2(ratios[i]) - i + 1));
  
  const bin14 = rate.toString(2).padStart(14, "0");
  const bin16 = `0${bin14.slice(0, 7)}0${bin14.slice(7)}`;
  const hex = parseInt(bin16, 2).toString(16).toUpperCase().padStart(4, "0");

  bytes.push(`${hex.slice(0, 2)}h ${hex.slice(2)}h `);
}

bytes = turnArray(bytes, 12 - baseIndex);
message += `${bytes.join("")}F7h`;

console.log(message);

5. おしまい

7平均律の短いメロディを作ってみました。
私の耳が壊れたからかもしれませんが、意外と違和感なく聴けると思います、多分。

もし12平均律以外の音律に興味を持っていただけたら幸いです、とくに12未満の。