高次ボロノイ図とは？
平面状の複数の母点が存在し、ある母点への距離が最も短くなるような領域がボロノイ図です。一方でn次のボロノイ図とは、ある母点への距離が各母点への距離のなかで1~n番目に短くなるような範囲を意味します。言葉だけでは分かりにくいので図を見てください。まず下図のようにボロノイ分割される母点の集合を例に考えます。
中央にある青色で示した点に注目して2,3,4次のボロノイ図を描画すると次のようになります。
高次ボロノイ図の特徴
- n次の範囲の点は注目するある母点（以降、中心点と呼称）との距離がすべての母点との距離の中でn番目以内に短い。
- 1次ボロノイ図は通常のボロノイ図に対応する
- ボロノイ図の各辺は、中心点と各母点を結ぶ線分の垂直二等分線が互いに分割する線分である。
2点から等距離にある点の集合である垂直二等分線が境界線となるは自然に感じますね。下の図で2次の例を示します。黒で示す各母点と青色の中心点の二等分線を描き、それらの交点で分割される線分をうまく結ぶと太線の多角形が求める範囲になります。
- ある二等分線が他の二等分線との交点で分割された２線分がそれぞれm,n次ボロノイ図の辺であるとする。このとき、次数の差|m-n|は1である。
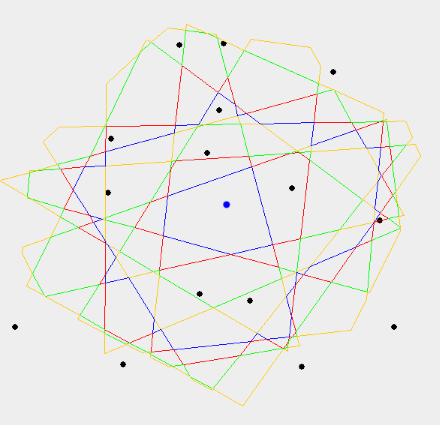
ボロノイ図の次数とは「中心点への距離がどれだけ近いかの指標」と直感的に解釈できます。ですから先にも説明した通り垂直二等分線を跨ぐと次数が変化しますが、突然2以上変化することはありません。次の図は内側から順に1次から8次までを色分けして描画したものです。1本の直線に注目すると各交点での次数の変化（＝色の変化）は1であるのが分かると思います。
さらに交差する２つの二等分線がどの母点と中心点のものか調べれば、次数が±1のどちらへ変化するか符号も判別できます。いま下の図のように中心の点$C$と母点$P$の垂直二等分線を考えます。他の母点$P'$との二等分線$L'$によって2つの線分$L_1$と$L_2$に分割されているとき、分割された線分のうち直線$L'$に対し点$C$と異なる側にある線分の方が他方より次数が1高いと判定されます。この図の場合は点$C$の反対側にある線分$L_1$の方が$L_2$より次数が1高くなります。
これらの特徴を生かして描画アルゴリズムを考えます。
描画アルゴリズム
中心点と母点の垂直二等分線を描き、それらの交点を頂点、交点が分割する線分を辺にもつグラフ構造を考えます。仮にn次のボロノイ図が既知なら各頂点における次数の変化量に従って線分を辿れば(n+1)次も計算できます。こうして1次からn次まで逐次的に求めていきます。
準備
まず中心点と各母点の垂直二等分線を引きます。求める次数や母点の分布状況によってはすべての母点に関して考える必要はありませんが、後続の処理を行うのに十分な数だけ用意されたと仮定します。
そして二等分線の交点と分割された線分から成るグラフ構造を計算し記録しておきます。各頂点には線分×4が接続されおり、一直線上に移動した時の次数変化±1が計算済みとします。下の図は青い中心点と各二等分線を描いたもので、各交点では次数が+1増える方向に赤い矢印を描いて表現しています（見やすさのため必要最小限の二等分線と矢印のみ示します）。
1次ボロノイ図の探索
逐次的に求めるための開始ポイントとして1次のボロノイ図をまず準備します。ドロネー三角分割から求めるのが一般的ですが、ここでは用意したグラフを使って計算してみましょう。簡単です、どこでも適当な辺から始めて頂点に達したら、
- 辿ってきた線分が乗っている二等分線とは別の直線上にある
- 頂点から見て次数が-1減少する方向
を満たす辺を次に辿ります。下図のような例で試してみましょう。適当な場所から始めて交点では矢印方向と反対方向へ進んでいくと、
必ず中心点の方へ近づいていき、ある時から同じ頂点をぐるぐる巡回し出します。その経路上の辺こそが1次ボロノイ図です。
(n+1)次ボロノイ図の探索
いまn次ボロノイ図が既知とします。その多角形の頂点のうち(n-1)次ボロノイ図と共有していないものをひとつ適当に開始点として選びます。選んだ頂点から辺を辿り別の頂点に達したら、
- 辿ってきた線分が乗っている二等分線とは別の直線上にある
- 頂点を経て次数が変化しない方向
を満たす辺を次に選んで辿ります。下図のように青線の1次ボロノイ図が与えられており次の2次ボロノイ図を探す例を示します。1次ボロノイ図の適当な頂点を選んで次数が+1増加する方向へ探索を開始し、交点では次数変化が±0となるように進んでいくと、
最後には開始した頂点に戻ってきますので閉じた多角形が得られます。二つ目の条件「次数が変化しない」は分かりにくいですが、図のように矢印の方向で頂点にやって来たら矢印と反対の方向へ出ていく、逆に矢印反対方向に頂点に入ったら矢印方向に出ていく、という要領です。
実験
具体的なデータで描画してみます。
使用したデータ
日本の鉄道駅のデータを駅データ.jpから利用。9000くらい存在する駅の位置座標を使います。
注意 以降の実験では簡単のため経度・緯度を直交座標平面のXY座標に読み替えています。投影した平面での直線は実際の球面上の直線（測地線）とは対応しません。また経度・緯度でユークリッド距離を計算するというヤバイ実装なので高緯度では東西方向の距離が実際の値より誇張されるのに留意してください。
結果
駅の密集する新宿駅の座標をターゲットに指定して18次まで描画。分かりやすさのため1次から順に青、緑、赤、黄色でそれぞれ描画しています。図を見れば各地点から新宿駅が他の幾つの駅より近いかが一目瞭然です。また近接する多数の駅に圧迫され、各次数の多角形が細かく屈折し幅が狭くなっている様子が分かります。
アルゴリズムの問題点
このままでは幾つか実用上の問題があります。
- どの範囲の母点まで考えて垂直二等分線を引けば済むか？
（母点の数）＝（二等分線の数）の二乗に比例する数の交点を計算しグラフを構築する必要が生じます。最初に全部の二等分線を計算する方針だと母点の増加で計算量がすぐに爆発します。 - ボロノイ図の多角形が閉じない場合がある。
1次の場合と同様に高次でも閉じない場合があり得ます。その時の対応を別に用意する必要があります。