無線通信のシミュレーションを行う際、最悪のケースである、完全な見通し外における通信を前提とする場合が多いと思います。完全な見通し外通信の通信路行列はレイリーフェージング通信路と呼ばれ、「受信信号の振幅値はレイリー分布に」「位相の回転角は一様分布に」したがうような変動が生じます。
すなわち、雑音が存在しない場合,受信信号$y_k$はレイリー分布に従う乱数$r_k$と一様分布に従う乱数$\theta_k$を用いて以下のように表すことができます。
y_k = r_k e^{j\theta_k} x_k
では、レイリーフェージング通信路におけるシミュレーションを実行するためには$r_k$と$\theta_k$という乱数を生成して上のような計算をすればよいのでしょうか。
それでもおそらくできますが、時間を大幅に無駄にしてしまう可能性があります。
なぜかというと,$r_k e^{j\theta_k}$の代わりに平均0、分散1の複素ガウス分布に従う乱数$h_k$を掛けたらいいからです。
とりあえずそのコードを貼ります。
import matplotlib.pyplot as plt
from numpy.random import *
import numpy as np
symbol_length = 256000 # 各送信アンテナから送るシンボルの数
M = 2 # 送信アンテナ数
N = 2 # 受信アンテナ数
TX_bit = randint(0, 2, (M, symbol_length)) # ビット列の生成
# BPSK変調
TX_BPSK = np.zeros(TX_bit.shape)
TX_BPSK[TX_bit == 0] = -1
TX_BPSK[TX_bit == 1] = 1
RX_BPSK = np.zeros([N, symbol_length]) + 1j * np.zeros([N, symbol_length])
for i in range(symbol_length):
# 見通し外の無線通信路(レイリーフェージング通信路)に対応する通信路行列の生成
H = (randn(N, M) + 1j * randn(N, M)) * 1 / np.sqrt(2)
# 送信
temp = np.dot(H, np.reshape((TX_BPSK[:, i]), (M, 1)))
RX_BPSK[:, i] = np.reshape(temp, N)
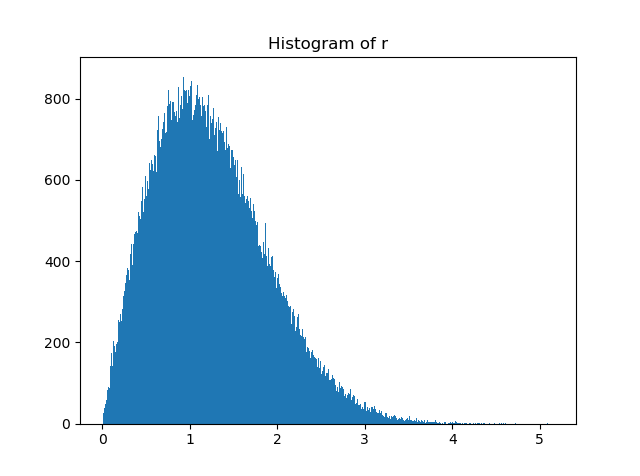
plt.hist(np.abs(RX_BPSK[0, :]), bins=1000)
plt.title('Histogram of r')
plt.show()
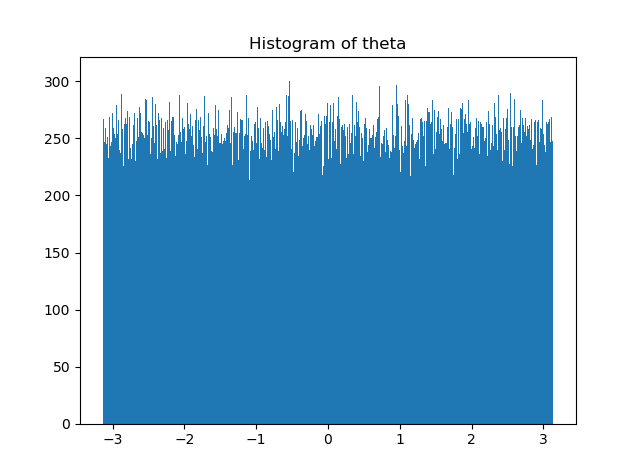
plt.hist((1j * np.log(RX_BPSK[0, :])).real, bins=1000)
plt.title('Histogram of theta')
plt.show()
大事なのは真ん中あたりの
H = (randn(N, M) + 1j * randn(N, M)) * 1 / np.sqrt(2)
です。これが平均0、分散1の複素ガウス分布に従う乱数を生成している部分です。
結果として、
というヒストグラムが出力されます。たしかに振幅値はレイリー分布に、位相の回転角度は一様分布に従っていることがわかるかと思います。
上の例では各時刻$i$において通信路状態がリセットされるシミュレーションをしていますが、実際には十分短い間では通信路状態は変動しないという仮定を置いて、for文を使わずに
H = (randn(N, M) + 1j * randn(N, M)) * 1 / np.sqrt(2)
RX_BPSK = np.dot(H,TX_BPSK)
というような形で受信シンボルを計算することのほうが多いかと思います。
この方法で振幅がレイリー分布に従うようになることの証明
まずは
h_k = r_k e^{j\theta_k} = a_k + jb_k
とおきます。我々の目標は$f_{r_k}(x)$という確率密度関数を求めることなので、$r_k = (a_k^2 + b_k^2)^{\frac{1}{2}}$を利用して,
\begin{align}
f_{r_k}(x) &= f_{ (a_k^2 + b_k^2)^{\frac{1}{2}} }(x) \\
&= \frac{d}{dx} P( (a_k^2 + b_k^2)^{\frac{1}{2}} < x) \\
&= \frac{d}{dx} P( a_k^2 + b_k^2 < x^2) \\
& = 2xf_{a_k^2 + b_k^2}(x^2)
\end{align}
という感じで変形していきます。$a_k$、$b_k$はそれぞれ独立な平均0、分散1/2のガウス分布に従うので、${a_k^2} \sim b_k^2 \sim {{\rm N}\left(0,\frac{1}{2}\right)^2}\sim{\Gamma\left( \frac{1}{2},1\right)}$となります。
さらにガンマ分布の再生性より、$a_k^2 + b_k^2 \sim \Gamma\left( \frac{1}{2}+\frac{1}{2},1\right) = \Gamma\left( 1,1\right) $となることを考えると、
\begin{align}
f_{a_k^2 + b_k^2 }(x) &= f_{ \Gamma\left( 1,1\right) }(x) = e^{-x}
\end{align}
となります。これを$f_{r_k}(x)$の式に代入すると,
\begin{align}
f_{r_k }(x) &= 2xe^{-x^2}
\end{align}
となり、これは$\mathbb{E}[r_k^2]=1$、すなわち電力が保存されるという条件付きのレイリー分布に従う乱数の確率密度関数です。