【python】BPSK変調・AWGN通信路におけるシミュレーションの方法と気を付けるべきこと

pythonで通信系のシミュレーションする人がどれだけいるのかよくわかりませんが、個人的なpythonの練習の意味も含めてBPSK変調・AWGN (Additive White Guassian Noise)通信路での通信シミュレーションの方法について書きたいと思います。

僕が研究を始めて間もないころに戸惑った
・雑音分散とSNR(Signal to Noise Power Ratio)の関係
・判定誤りが発生するときのイメージ
について少し詳しめに書きます。

先にコードの全体を貼り付けておきます。

import numpy as np

# 送信側アンテナ数
M = 2
# 受信側アンテナ数
N = 2
# 送信ビット数
bit_num = 10 ** 3

# Additive Gaussian White Noiseの生成する際のパラメータ設定
SNRdB = 10
SNR = 10 ** (SNRdB / 10)
No = 1 / SNR

# 送信ビット列を生成
TX_bit = np.random.randint(0, 2, (M, bit_num))

# 0 -> -1, 1 -> 1としてBPSK変調
TX_BPSK = np.ones((M, bit_num))
TX_BPSK[TX_bit == 0] = -1

# AWGN雑音の生成
noise = np.random.normal(0, np.sqrt(No / 2), (M, bit_num)) \
        + 1j * np.random.normal(0, np.sqrt(No / 2), (M, bit_num))

# AWGN通信路 = 送信シンボル間干渉が生じないような通信路で送信
RX_BPSK = TX_BPSK + noise

# 以下のprint関数の出力を表示すると、Noとほぼ一致するはず
# print(np.dot(noise[0, :], np.conj(noise[0, :]))/bit_num)

# 受信信号をビットに判定
RX_bit = np.zeros((N, bit_num))
RX_bit[np.real(RX_BPSK) > 0] = 1
RX_bit[np.real(RX_BPSK) < 0] = 0

error_sum = np.sum(np.abs(TX_bit - RX_bit))
BER = error_sum / (M * bit_num)

#解説

##初期パラメータ設定
頭の

# 送信側アンテナ数
M = 2
# 受信側アンテナ数
N = 2
# 送信ビット数
bit_num = 10 ** 3

については、シミュレーションの本質的な内容とは関係のないパラメータたちです。
一応、今後AWGN通信路からレイリーフェージング通信路に拡張することも考えて送受信アンテナ数は別々で設定できるようにしてありますが、このコードに限って言えば、N=Mでないと回らないので注意してください。また、NやM、bit_numの値を大きくすればするほどBER(Bit Error Rate)は理論値に近づきます。

##雑音電力の決め方
むずかしいところは

# Additive Gaussian White Noiseの生成する際のパラメータ設定
SNRdB = 10
SNR = 10 ** (SNRdB / 10)
No = 1 / SNR

から始まります。
通信系のシミュレーション結果を表示する際は、横軸にSNR[dB]、縦軸にBERをとったグラフ、すなわち「どれだけの電力が使われたとき、どれだけ正確な通信ができたかを表すグラフ」が基本となります。SNR[dB]が小さい値であればBERは高く(0.5に近い値)なり、SNR[dB]が大きければBERは小さく、理想的には0になります。

そしてそのようなシミュレーションをするためには、適当な大きさの電力を持つのAWGN雑音を発生させる必要があるわけです。

その「適当な電力」を決めているのが上記のコードで、この部分をあえて数式で書くと、

\begin{align}
{\rm SNR[dB]} &= 10{\rm log}_{10} \frac{1}{N_{\rm 0}} \\
{\rm SNR} &= 10^{\frac{1}{10} \times 10{\rm log}_{10} \frac{1}{N_{\rm 0}}} \\
&= 10^{{\rm log}_{10} \frac{1}{N_{\rm 0}}} \\
&= \frac{1}{N_{\rm 0}} \\
N_{\rm 0} &= \frac{1}{\rm SNR}
\end{align}

という形になります。
ちなみに、1行目の「1」は「送信電力を基準である『1』とする」という意味です。
通信シミュレーションを行うときには、このように送信電力を基準となる「1」に固定した上で、雑音電力を決めます。
私の数式の１行目で「1」としてある部分を$E_{\rm s}$としてある数式も世の中にはたくさんありますが、意味しているところは大体一緒です。とにかく、送信電力と雑音電力を別々に設定するのではなく、送信電力を基準に雑音電力を決めるのが原理原則であると認識しておくといいかなと思います。

##ビット列の生成とBPSK変調
次に、

# 送信ビット列を生成
TX_bit = np.random.randint(0, 2, (M, bit_num))

# 0 -> -1, 1 -> 1としてBPSK変調
TX_BPSK = np.ones((M, bit_num))
TX_BPSK[TX_bit == 0] = -1

という部分ですが、これは特に言うべきことはないと思います。
今回はBPSK変調を施していますが、QPSK変調や64QAM変調などにしたい場合はここを書き換えることになります。

##複素雑音を生成するときに注意しなければならないこと

# AWGN雑音の生成
noise = np.random.normal(0, np.sqrt(No / 2), (M, bit_num)) \
        + 1j * np.random.normal(0, np.sqrt(No / 2), (M, bit_num))

ここもまた混乱しがちな部分です。ポイントは、
①実数成分だけでなく、複素成分も持つ雑音を生成した理由
②np.sqrt(No / 2)が「No」ではなく「No/2」である理由
のふたつかなと思います。

まず①についてですが
参考書によっては、実数領域だけで扱っている本もありますし、それはそれで全くもって正当です。どちらかというとそのパターンのほうが多いと思います。
ただ、今回は複素雑音がかかるという前提を置きました。それは今後シミュレーションを拡張する場合、雑音は複素数で生成しなければならないからです。
そのうち変調達数を増やせるシミュレーションの記事も書くので、詳しくはそれまでお待ちいただければと思います。

次に②についてですが、
これは雑音電力がNoとなるためには、実数成分と複素成分の電力がそれぞれNo/2でなくてはならないからです。
たとえば、雑音$z$が

z = a + jb

というかんじで実数$a$と$b$に分けられるとしましょう。
この$z$の分散=雑音の電力、すなわち$\mathbb{E}[|z|^{2}]$がNoであってほしいわけです。
複素数の絶対値の定義と、$a$も$b$は互いに独立であり平均0である正規分布に従うことに注意すると、

\mathbb{E}[|z|^{2}]= \mathbb{E}[|a|^{2}] + \mathbb{E}[|b|^{2}] \\
(|z|^{2} = (a + jb)(a - jb))

となりますよね。だからこそ、$a$の分散=$\mathbb{E}[|a|^{2}]$、$b$の分散=$\mathbb{E}[|b|^{2}]$はそれぞれNo/2として設定しておかなければならないのです。

# 以下のprint関数の出力を表示すると、Noとほぼ一致するはず
# print(np.dot(noise[0, :], np.conj(noise[0, :]))/bit_num)

の部分をコメントアウトすると理解の一助になるかもしれません。bit_numが十分に大きいとき、noiseの分散 = zの分散はNoに一致するはずです。逆に、仮に

noise = np.random.normal(0, np.sqrt(No), (M, bit_num)) \
        + 1j * np.random.normal(0, np.sqrt(No), (M, bit_num))

というふうに雑音を生成してしていたとしたら、printの結果は2Noに近い値になるはずです。

##受信シンボルの判定

# 受信信号をビットに判定
RX_bit = np.zeros((N, bit_num))
RX_bit[np.real(RX_BPSK) > 0] = 1
RX_bit[np.real(RX_BPSK) < 0] = 0

BPSK変調信号の場合、その複素成分に関しては無視し、実数成分が0以上/以下で判定を行います。

たとえば、以下の図はSNR = 10[dB]でシミュレーションを行った時の受信信号のコンスタレーション(配置)です。

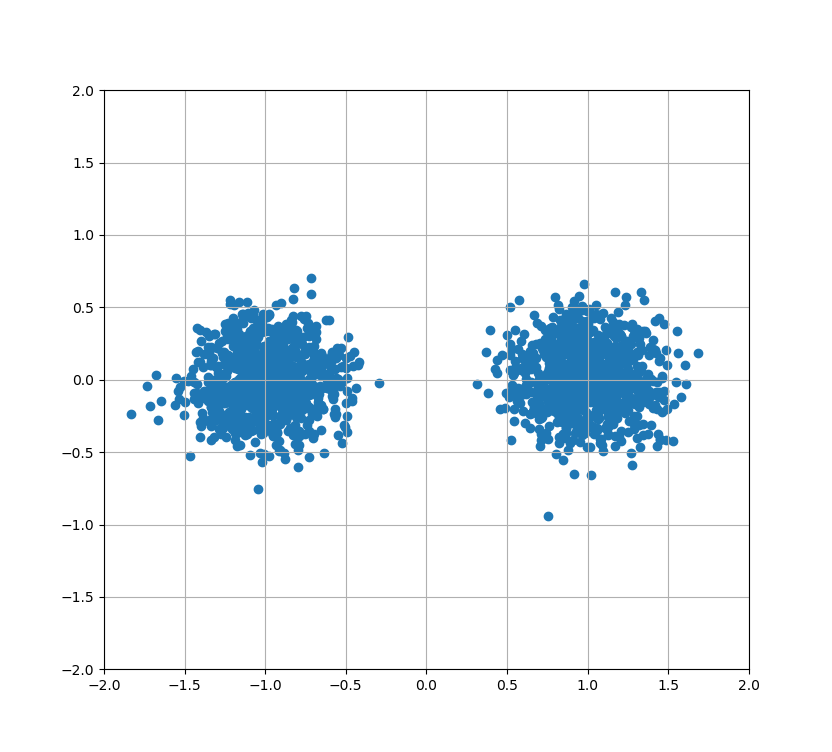
ご覧の通り、真ん中(実数値が0のライン)を割って反対側にいっている点はほとんどありません。
次の図はSNR = 5[dB]のときの図です。

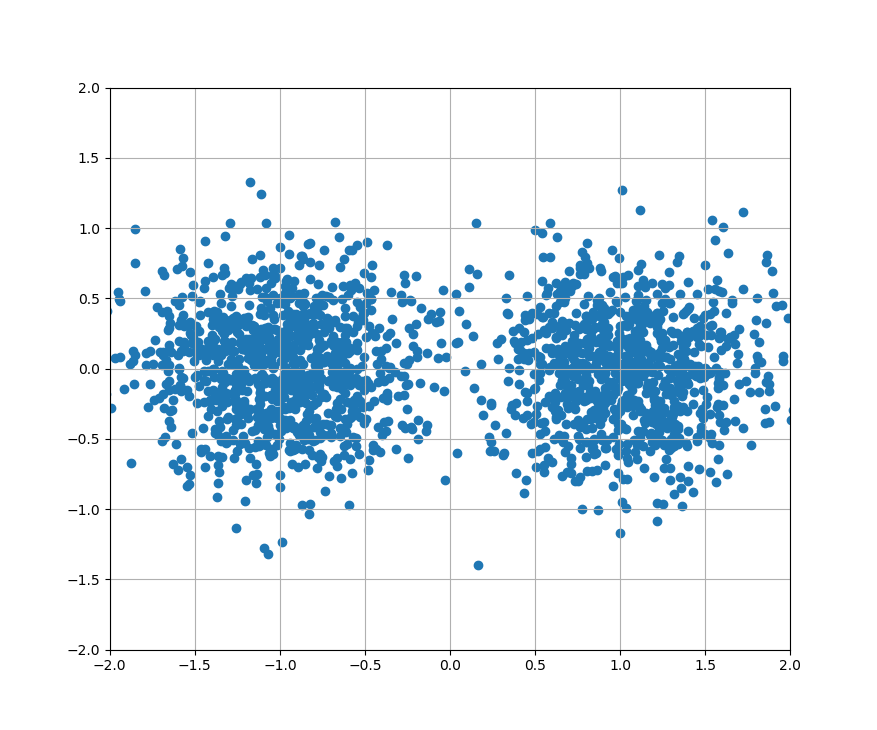
だんだん雲行きがあやしくなってきました。
そして最後に、SNR = 0[dBのときの図です。

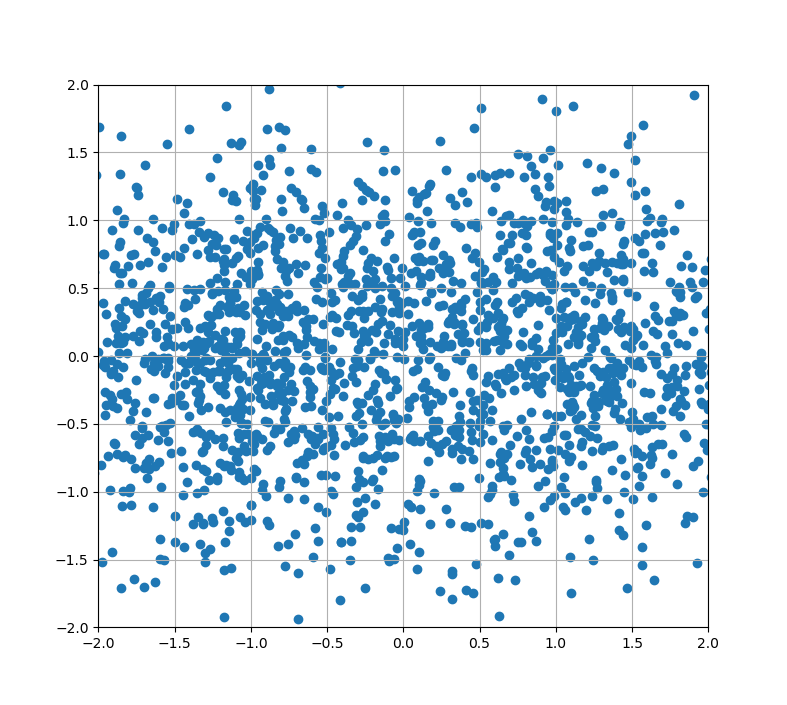
もうお分かりとは思うのですが、これらの図の点のうち、真ん中を割ってしまった点が判定誤りとなります。
SNR = 0[dB]のときなんか、これはもはや通信どころではありません。
多値QAMの場合の判定も基本的には同じです(その場合は複素成分でも判定領域を分割します)。

ちなみに、「雑音分散が$N_0$である」ということは、「送信シンボル点からズレるユークリッド距離が$\sqrt{N_0}$以内である確率が66%である」ということです。
理由については、正規分布と標準偏差の関係について調べてみるとわかるかなと思います。

##BERの計算

error_sum = np.sum(np.abs(TX_bit - RX_bit))
BER = error_sum / (M * bit_num)

最後に、BER = 何bit送信して、そのうちいくつが判定誤りを起こしたかを計算しています。
以外の初学者のうちはnp.absを忘れてしまう気がします。私もいまだに忘れます。

また、テクニックのひとつなのですが、プログラムにバグが無いかチェックするために「最も劣悪な条件で通信した場合、BERが0.5になるかどうか」をみるのは非常に有効です。
たとえば、SNR = -100[dB]にしているにも関わらずBERが0.1とかなのであれば、確実にどこかにバグがあります。

##まとめ
本稿ではBPSK変調・AWGN通信路でシミュレーションをする方法、そのうえで気を付けるべきことについてお話しました。
私は通信の勉強をはじめてすぐのころは「分散の定義」すらわかりませんでした。
今もまだ通信というものを語れる状態にはほど遠いですが、専門用語の定義を逐一確認したり、コード・数式の必然性というものにこだわって理論を追っていくと少しずつ楽しくなるかなと思います。