Go to Qiita Advent Calendar 2024 Top
LoginSignup
1
1

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

@Schumi

論文紹介 - Managing Risk of Bidding in Display Advertising

Last updated at Posted at 2019-04-10
  • 社内の勉強会で使ったやつの焼き直しです。

TL;DR;

  • Managing Risk of Bidding in Display Advertising (WSDM'17) の紹介 論文リンク
  • (CPC課金において) CTR予測を高く見積もって入札したときの赤字リスクの削減を金融工学的アプローチを考慮した二種の入札ロジック(VaR, Risk Management Profit )で考える
  • CTR予測をBayesian Logistic Regeression + ラプラス近似 で 分布推定し, 予測の標準偏差を入札に利用する。
  • 既存入札ロジック (Logistic regression + Linear bidding) 比で , 実験対象のキャンペーン全体で見たときにiPinYou で オフライン検証 Profit + 15.4%, 匿名DSPのオンライン検証で 17.5% Profit 上昇

モチベーション

問題定義 Risk of Bidding (4.1 より)

変数定義

  • $ \hat{y} \sim p_\hat{y}(\hat{y})$ : 予測CTR
  • $v$ : 広告主が定義するuser action (click, conversion の価値) = CPC単価
  • $r = v \cdot \hat{y}$ : utility, impression の価値
  • $z \sim p_z(z)$ : market price(= second price)
  • $b$ : 自DSPの入札価格
  • $R(b)$ : Profit

Truth-telling bidding

  • Truth-telling bidding : 予算制約やオークションのボリュームを考慮しないケース

  • Profit $( v \cdot \hat { y } - z )$ を最大化する場合, (14) ~ (18) より $ \mathbb{E}[r] = v \cdot \mathbb{E}[\hat{y}] $が最適な入札価格

  • キャンペーン予算とオークションボリュームを考慮する場合は 補正係数$\phi$ をかけて, $\phi \cdot \mathbb{E}[r]$ を考える。

Discussion of Risk

  • $v \cdot \hat{y} < z $つまり $R[b] < 0 $となるケースは赤字となる
  • P(R(b)<0) の算出は以下式(19)
P ( R ( b ) < 0 ) = \int _ { 0 } ^ { 1 } p _ { \hat { y } } ( \hat { y } ) P ( b > z > v \cdot \hat { y } ) d \hat { y }= \int _ { 0 } ^ { 1 } p _ { \hat { y } } ( \hat { y } ) \int _ { v \cdot \hat { y } } ^ { b } p _ { z } ( z ) d z d \hat { y } \tag{19}

具体例でシミュレーション

  • 予測CTR分布

    • 式(12) で $\sum _ { i } \mu _ { i } x _ { i } = - 1 , \sum _ { i } q _ { i } ^ { - 1 } x _ { i } = \frac { 1 } { 3 }$ とする
    • このときCTRの期待値は 0.283

  • market price

    • 対数正規分布で, $\mu = 4 , \sigma = 0.5$

  • click value = 300

profit dist.png

  • 先述の truth-telling bidding では 84 での入札が最適だが, 16.7 % の赤字リスクを負う

  • $\hat {y}$ の標準偏差(分散)が大きいと, この赤字リスクは大きくなる -> VaR などの予測の分散を考慮した入札戦略を考える。

提案手法

前提知識

Baysian Logistic Regression

  • 単純に Logistic Regression の ベイズバージョン, 分布推定可能
  • 今回の論文では ラプラス近似を用いて, 閉形式で 予測CTR分布を導出 (12)
  • 式の導出は PRML と同様なので省略
  • 本文献中では オンライン環境でどうベイズ更新したかは書いていなかった :cry:

linear bidding

  • pCTRに予算制御などを考慮した, 係数をかける入札戦略

VaR

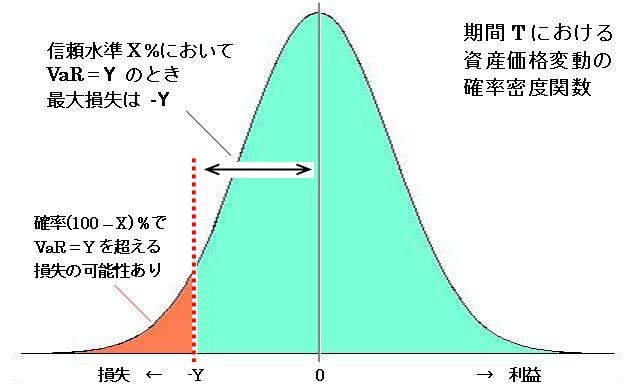
Value at Risk

バリュー・アット・リスクは、ある期間 $T$ における資産価値の損失リスクを推定した値で、統計上の信頼水準 $X %$において推定される最大損失 $Y$のことである
https://ja.wikipedia.org/wiki/バリュー・アット・リスク より
VaR_ja.JPG

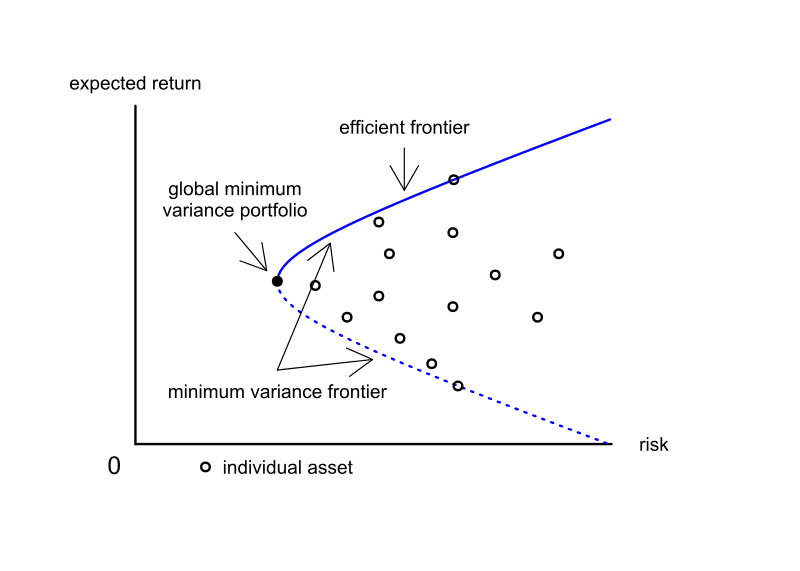
効率的フロンティア

方程式(1)をリスク・リターン平面上で図示したものを最小分散フロンティア(英: minimum variance frontier)と言う。
さらに最小分散フロンティアにおいて大域的最小分散ポートフォリオより上側の部分の曲線を効率的フロンティア(英: efficient frontier)と呼ぶ
https://ja.wikipedia.org/wiki/現代ポートフォリオ理論 より

Minimum_variance_flontier_of_MPT.svg.png

提案手法

lem1. Cantelli's Inequality

$P ( r < \mu - \alpha \sigma ) < \frac { 1 } { 1 + \alpha ^ { 2 } } \tag{20}$

チェビシェフの不等式の仲間, 確率分布のtailの確率のbound
これを使って, 2種類の入札ロジックを考える

Bidding with Value-at-Risk(VaR) utility

VaRの派生として, VaR utility を以下の式で考える

\tilde { r } = \mathbb { E } [ r ] - \alpha \operatorname { Std } [ r ] \tag{21}

このとき, 実utility $r < \tilde { r } $ となる確率は, lem1より $\frac { 1 } { 1 + \alpha ^ { 2 } }$ でboundされる。

このとき, (18)は以下のように変形される。

b _ { \mathrm { VaR } } ( r ) = \tilde { r } = v \cdot ( \mathbb { E } [ \hat { y } ] - \alpha \operatorname { Std } [ \hat { y } ] ) \tag{22}
  • $ \alpha$の各場合について以下のように名付け
    • $\alpha < 0$ : risk seeking リスク追求(強気入札)
    • $\alpha = 0$ : risk neutral リスク中立(通常入札)
    • $\alpha > 0$ : risk averse リスク回避(弱気入札)

式(12)から直接導かず, lem1を経由して, VaR入札戦略を決めた理由は以下

  1. 解析的なCTR予測分布でなくても適用可能
  2. $\alpha$ を定数パラメータとして扱うことで計算が効率的に行える

さらに, campaign budgetを考えるための係数 $\phi$ を考えるので実際の入札額は以下のように決まる。

b _ { \mathrm { VaR } } ( r ) = \phi \cdot v \cdot ( \mathbb { E } [ \hat { y } ] - \alpha \operatorname { Std } [ \hat { y } ] )

Bidding for Risk Management Profit

VaR 以外のアプローチとして直接profit R(b) を最適化する方法とそのリスクの考慮を考える。

profit R(b)は以下の式で表される。

R ( b ) = \left\{ \begin{array} { l l } { 0 } & { b \leq z \quad ( \operatorname { lose } ) } \\ { v \cdot \hat { y } - z } & { b > z }  \quad ( \operatorname { win } )  \end{array} \right.  \tag{23}

※ $\hat{y} , z$ が確率変数であることに留意

R(b)についても, lem1 からrisk のboundを考えるための VaR Profit を以下で定義

$\tilde { R } ( b ) = \mathbb { E } [ R ( b ) ] - \alpha \operatorname { Std } [ R ( b ) ] \tag{24}$

このとき, 入札額 $b_{RMP}$は以下の式から導出される

$b _ { \mathrm { RMP } } ( R ( b ) ) = \underset { b } { \arg \max } \mathbb { E } [ R ( b ) ] - \alpha \operatorname { Std } [ R ( b ) ] \tag{25}$

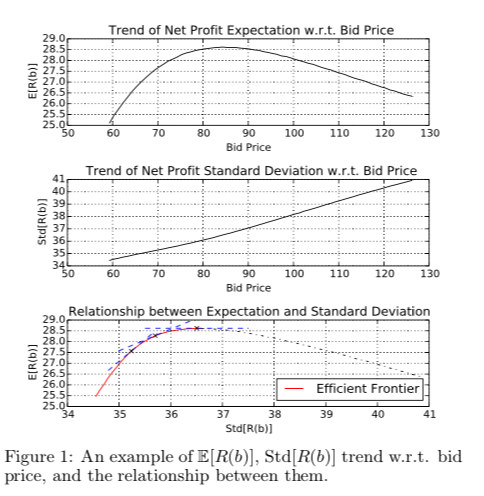
$ \mathbb { E } [ R ( b )$ と $\alpha \operatorname { Std } [ R ( b ) ]$ は非自明な trade offを持つので, bは Efficient Fontierに基づき決定する。

supple fig1.png

詳細は 参考資料 1 を参照

実験

オフライン検証(iPinYou)

データセット

  • 2013年に公開された open dataset, 10日分, 9キャンペーン 19.5M imps, 14.89K clicks の配信ログ
  • 後半3日がテスト用のデータとなっている

実験プロトコル

  • CTR予測モデルは training dataで学習
  • ハイパーパラメータ $\alpha, \phi$ はtest data の前半をsplitしたvalidation dataを用いて調整
    • $\phi$ : 予算制約およびオークションボリューム考慮のための係数
    • $\alpha$ : risk をどの程度考慮するかの係数
  • 残りのテストデータで パフォーマンスをテスト
  • CPC単価はキャンペーン単位でtraining データのCPCの平均を利用
  • テストの入札リクエストが尽きた場合, もしくはキャンペーン予算を使い切ったときにテストは打ち切られる

比較した手法

  • LR + Linear Bidding
  • VaR
  • RMP

Evaluation Measure

  • campaign profit
  • campaign ROI
    • profit/cost
  • CPM
  • win rate
  • CTR
  • eCPC
  • Cost - Penalized profit
    • この論文で著者が定義したmetrics
    • パフォーマンスとコストは通常トレードオフなので, いくつかの$\lambda$ に対して, この値をみてハイパーパラメータ $\alpha, \phi$ をチューニング(5.5で説明)
profit -  \lambda \space cost 
(= total\_click\_value -  (1+\lambda) \space cost)

Profit and Cost analysis

  • ハイパーパラメータ $\alpha, \phi$ チューニングのために様々な条件下でのprofit- cost のトレードオフを分析
  • このとき $\phi = 1$ としてOK
  • $ \alpha$の各場合について profit -cost トレードオフは以下
    • $\alpha < 0$ : risk seeking リスク追求(強気入札)
    • $\alpha = 0$ : risk neutral リスク中立(通常入札)
    • $\alpha > 0$ : risk averse リスク回避(弱気入札)

Non-Budgeted Settings

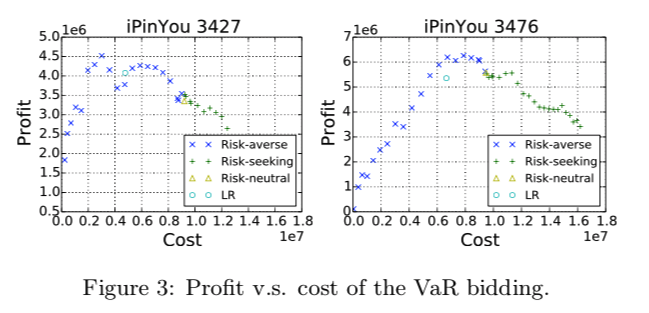
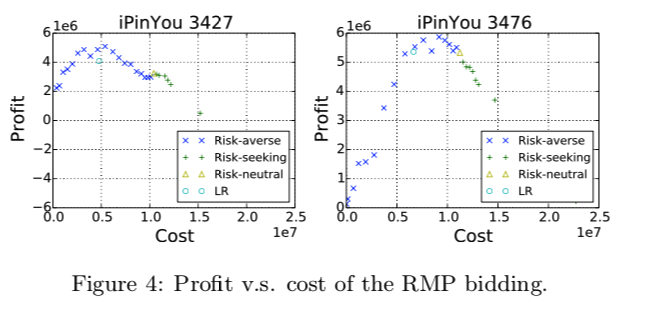
予算制約を考慮しない場合において, $\alpha$ を変化させたときのVaR bidding, RMP bidding のProfit とCost の関係は以下

fig3.png
fig4.png

  • 図のようにほぼ凸な形状になる, かつ peak は Risk-averse
  • 従って 経験的に Risk-averseがこの場合の支配戦略となる

Budgeted Settings

実環境では予算制約がある。
文献[38] と同様に複数パターンの予算制約でのパフォーマンスを評価するために, 予算を 1/2, 1/4, 1/8… として実験を行った。

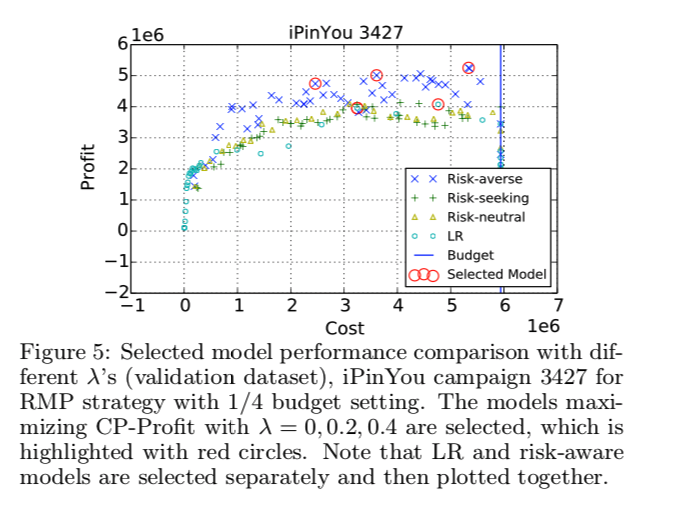
fig5.png

Selected model は CP-profit を用いて $\lambda = 0, 0.2, 0.4$ に対して$\alpha, \phi$ をチューニングしたもの, こちらもProfit でみた場合Risk-averseなモデルが支配的

Distinction with Lower Biddings

Risk-averse bidding とlinear biddingで入札を弱める戦略(Lower Bidding)の差を考える

当然, linear biddingでも全体の入札を弱めると, cost と profitの両方が低下し, ROIは増加する。

図5で示されたように, Risk-averse biddingでは Lowere Bidding と同等のコストで profit と ROI を増加させた。

この意味で Risk-averse なモデルのほうが, Lower bidding より優れている。

Bidding without Budget Constraints

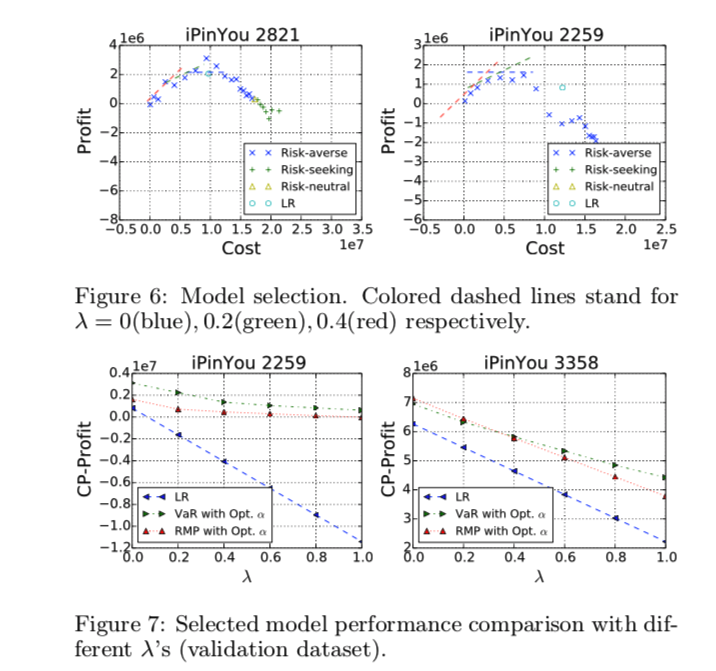
fig6,7.png

図6は $\alpha$ を変えて, Profit-Costの点をplotして それぞれの $\lambda$ に対して, CP-Profit を最大化するように, $\alpha$ を選択する方法

図7は それぞれの $\lambda$ に対して, LR と$\alpha$ をチューニングした VaR, RMPでのCP-Profit の比較

実験結果から以下の結論を得た

  1. VaR, RMPはいずれの場合もLRよりCP-Profitで優位
  2. 純粋なProfit を考える $\lambda =0$ のケースで, VaR, RMPはそれぞれLRに対して Profitを 50.7%, 25.1%改善した。
  3. 図7の $\lambda$ - CR-Profit でLRは直線的だが, VaR とRMP は凸 だったため, $\lambda$ が大きいほうが, ROIは大きくなる

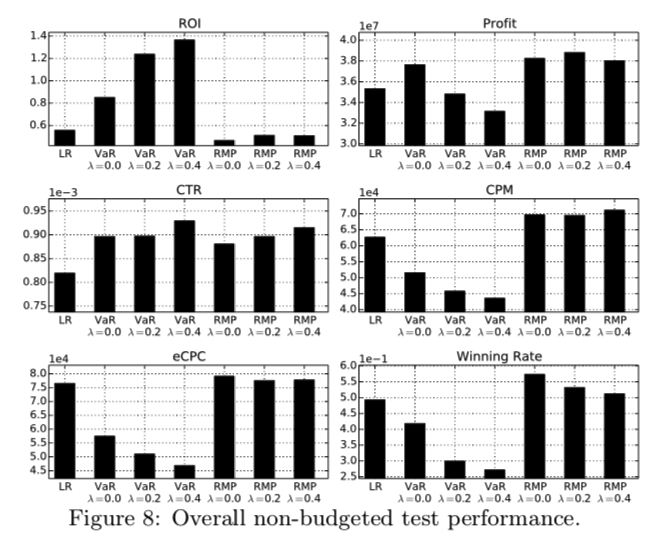
9つのキャンペーン全体での全体のKPIについては以下の通り

fig8.png

実験結果から以下の結論を得た

  1. 提案手法は 全体的にベースラインより 高いProfitを示した
  2. VaR はLRと比較して大幅にROI を改善した。
  3. RMPは$\lambda$ によらず, Profitは安定して10%改善した。これはRMPは直接Profitを最大化する戦略であるため。一方でCPMや eCPCは高騰したため ROIは低い
  4. 提案手法は 全てのケースで CTRを改善したが, これは CTR予測が不確実なものから確実なものに予算が割り振られたためと考えられる。

Bidding with Budget Constraints

それぞれの $\lambda$ に対して, $\alpha$ を図6の方法で選択した。選択したモデルは 図5の赤丸のもの。

$\phi$ はvalidation setでprofitを最大化するように選択した。

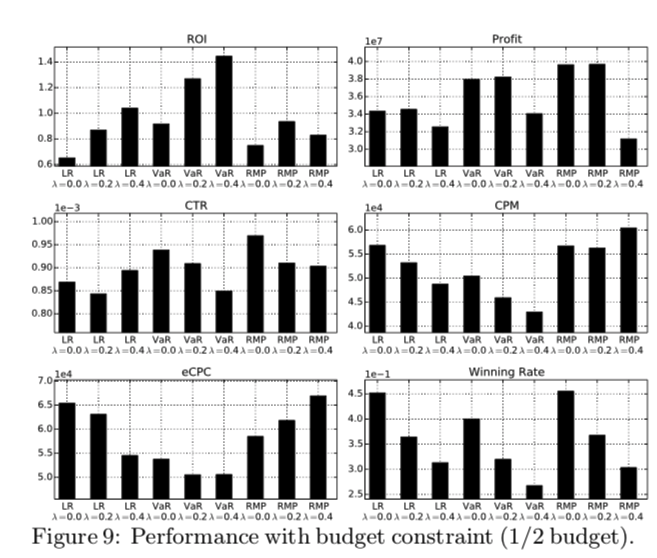
以下に予算 1/2で実験した結果のKPIを示す。

fig9.png

実験結果から以下の結論を得た

  1. $\lambda$ が小さいときは 提案手法の方が Profit が大きい。具体的にはLRでのCTR予測値が低いキャンペーンについて特にProfitを改善した。
  2. $\lambda = 0, 0.2$ で提案手法はともに LRより, ROIとProfit両方において優れた結果を示した。
  3. $\lambda = 0.4$ のVaR を除いて, 提案手法はいずれも CTRを改善した
  4. VaR はCPM, eCPC, WRいずれも低くなった, 一方RMPは CPM, eCPC, WRいずれも高くなった

オンライン検証(匿名DSP)

学習データについて

匿名のDSPにおいて, オンライン環境で提案手法を検証した。request の規模は 50B/day でCPCキャンペーンの有効なリクエストは 200M(4%), テスト用には 10CPCキャンペーンの1.5%のボリューム, つまり約3M/dayのbidを割り当てた。

トレーニング用の2016/01以前のデータは 424M imps, 532K clicks, 47.2K USD の利用が含まれていた。トレーニングデータのeCPCは0.087 USD。学習click dataは2%のnegative down samplingを行ったもの。

テストデータは全キャンペーンの平均CPC 0.54USDを入札時には指定した。

実験設定

2016/01 の7日間で以下の2つの戦略でABテストを行った。

  1. ベースラインのLR戦略, これは AUC 88%のLRモデルと, 運用者が設定した $\phi =0.56$ の線形入札関数となる。
  2. 提案手法のVaR戦略, $\alpha$ >0 は毎日微妙に変化させる(手作業でチューニング?) $\phi$ はLRより大きく設定した。
    (この $\alpha$ と $\phi$ の設定は入札価格を逆向きに調整するので, 結果的に平均入札額はbaselineに近い値)

それぞれに割り当てられたbidのボリュームは19.5M, 合計39M, 発生したimpは 3.3M, click は7.4Kだった。
VaRは $\phi$ の学習を行ったため, 予算は12%多く使用された。

結果の議論

実験結果

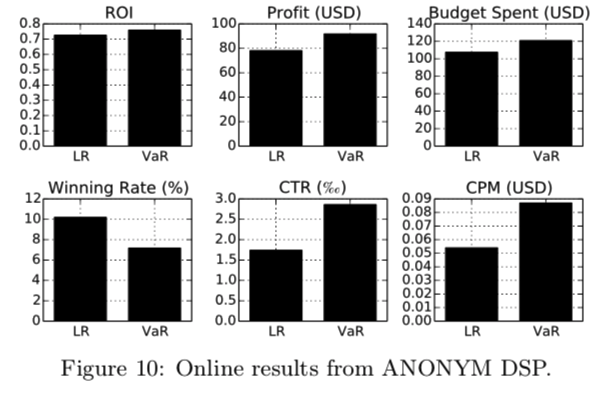
fig10

実験結果から以下の結論を得た

  1. ROIは+5%, この意味で提案手法の優位性は示される
  2. Profitは +17.5% (ただしbaselineより予算は多く投下している), リクエスト数は等しいので, 同一リクエストでROIを改善したい場合は役立つ。広告主は通常ROIに応じて予算を配分するため, 予算獲得には役立つ。
  3. WRは大幅に低下した。これは VaRによる入札額を低下させたrisky caseが入札額を増加させた confident caseより多かったためだと思われる。
  4. CTR は+ 64.4% と大幅に改善したため, 高品質なimpを買い付けられたと思われる。
  5. VaRでCPMは悪化した。これは高CTRの枠を買い付けるために入札額が高くなったことが原因と思われる。

conclusion

CTRの分布推定を行い, 推定値の分散を考慮した2種の入札モデル VaR, RMP でオフライン検証, オンライン検証のそれぞれでROI, Profit, CTRが改善しうることを示した。

future work

  • risk aware bidding の均衡市場分析
  • multi-frameなDynamic Creative はポートフォリオ最適化としてみなせる(?)
  • 広告表示によるuserの関心のupdateをmodelに組み込める(?)

  1. RMP biddingについての補足資料https://www.dropbox.com/s/qpv82dtrvdhk4zb/supplementary.pdf?dl=0 ↩

1
1
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
1
1

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?