概要
スマホのセンサーで云々をするという勉強をする中で、端末座標から世界座標に変換するということをしました. この記事はその備忘録です
スマホが静止している場合、世界座標では常に垂直下向きに 9.8m/s^2(重力加速度) がかかっているはずです.
しかし、スマホが傾いていた場合はスマホ目線(端末座標)では、場合によってはx軸が9.8m/s^2 だったり、y軸,z軸だったり...
そこで重力加速度をもとに端末座標を世界座標に変換しようということです.
複数の手段がありますが、今回は 回転行列 を使います
手順
手順は以下の通りです
- 重力加速度が掛かっている方向から垂直下向きを出す
- 垂直下向きと比較して各軸の傾きを出す
- 加速度を3次元ベクトルとし、傾きをもとに回転させる
- できた!!
今回使うデータ
0~4s: z軸正(画面が上)
6~8s: y軸正(端末を立てる)
10~14s: z軸正(端末を横向きに立てる)
最終的な結果
今回は端末のz軸正(画面が上を向いている状態)を基準とします.
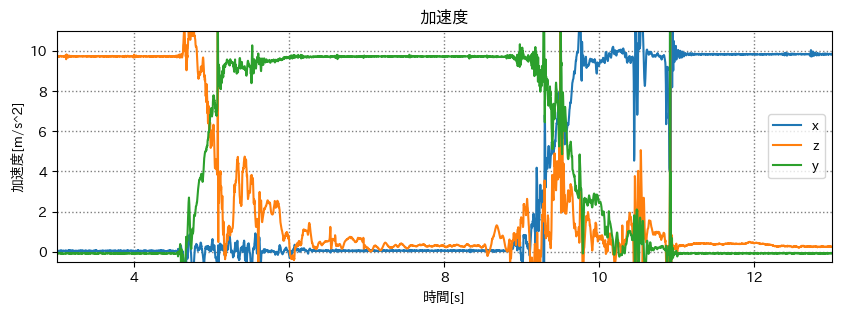
元の加速度
変換後の加速度
変換後は端末の傾きに関係なくz軸に 9.8m/s^2 が掛かっているのがわかります.
1. 重力加速度から垂直下向きを出す
加速度のcsvデータ
"Time (s)","Acc x (m/s^2)","Acc y (m/s^2)","Acc z (m/s^2)"
1.863478000E-2,5.264209956E-2,-9.212367237E-2,9.727422714E0
2.101644600E-2,4.307080805E-2,-8.733802289E-2,9.736993790E0
2.339811300E-2,5.264209956E-2,-7.776673883E-2,9.722636223E0
2.577983200E-2,4.307080805E-2,-8.733802289E-2,9.722636223E0
2.816149800E-2,4.366901144E-2,-9.690931439E-2,9.722636223E0
3.054316500E-2,3.828516230E-2,-8.733802289E-2,9.736993790E0
3.292483200E-2,3.828516230E-2,-8.255238086E-2,9.732208252E0
3.530649800E-2,5.742774159E-2,-7.776673883E-2,9.727422714E0
...
以上のcsvを pandas を用いて読み込みます.
df_acc = pd.read_csv(
"./log/Accelerometer.csv",
header=0,
names=("time", "x", "y", "z")
)
重力を出す
x,y,zの加速度からノルムを出すことで重力を出すことができます.
gravity = math.sqrt(x ** 2 + y ** 2 + z ** 2)
各軸の傾きを出す
各軸/重力 のアークコサインを使用することで 重力方向と各軸の傾き を出すことができます
tilt_angle_x = math.degrees(math.acos(x / gravity))
tilt_angle_y = math.degrees(math.acos(y / gravity))
tilt_angle_z = math.degrees(math.acos(z / gravity))
以上の計算を行うと以下のようなグラフを得ることができます.
端末の傾き
これをもとに加速度を回転させればいい...
というわけではありません!!
端末が基準の状態(z軸正が上向き)における各軸の傾きは
x軸: 90度
y軸: 90度
z軸: 0度
となります. 当然です!
それを反映させたグラフが以下の通りです

この傾きを元にベクトルを回転させます.
傾きをもとに回転させる
2次元ベクトルの回転
はじめに2次元ベクトルを回転させてみます.
θrad 回転する場合
$$
Vec^{\prime} =
\begin{bmatrix}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta \\
\end{bmatrix}
\begin{bmatrix}
x \\
y \\
\end{bmatrix}
$$
このように回転行列をかけてあげれば回転します. 簡単ですね!
では3次元のベクトルを回転させてみます
3次元ベクトルの回転
x軸周り
$$
R_x =
\begin{bmatrix}
1 & 0 & 0 \\
0 & \cos \theta & -\sin \theta \\
0 & \sin \theta & \cos \theta \\
\end{bmatrix}
$$
y軸周り
$$
R_y =
\begin{bmatrix}
\cos \theta & 0 & \sin \theta \\
0 & 1 & 0 \\
-\sin \theta & 0 & \cos \theta \\
\end{bmatrix}
$$
z軸周り
$$
R_z =
\begin{bmatrix}
\cos \theta & -\sin \theta & 0 \\
\sin \theta & \cos \theta & 0 \\
0 & 0 & 1 \
\end{bmatrix}
$$
3次元ベクトルは回転軸が3つあるため回転行列も3つあります.
$$
Vec^{\prime} =
\begin{bmatrix}
x \\
y \\
z \\
\end{bmatrix}
{\times}R_x
{\times}R_y
{\times}R_z
$$
これをpythonで書いてみます
(2,3,4) というベクトルを
x軸周りにx(rad)
y軸周りにy(rad)
z軸周りにz(rad)
回転させています
vec = [2, 3, 4]
r_x = np.array([
[1, 0, 0],
[0, np.cos(x), -np.sin(x)],
[0, np.sin(x), np.cos(x)]
])
r_y = np.array([
[np.cos(y), 0, np.sin(y)],
[0, 1, 0],
[-np.sin(y), 0, np.cos(y)]
])
r_z = np.array([
[np.cos(z), -np.sin(z), 0],
[np.sin(z), np.cos(z), 0],
[0, 0, 1]
])
vec = np.dot(r_x, vec)
vec = np.dot(r_y, vec)
vec = np.dot(r_z, vec)
最終的なコード
df_acc = pd.read_csv(
"Accelerometer.csv",
header=0,
names=("time", "x", "y", "z")
)
tilts = [] # 傾きを格納するリスト
# df を for で回す
for d in df_acc.itertuples(index=False):
time = d.time
x = d.x
y = d.y
z = d.z
gravity = math.sqrt(x ** 2 + y ** 2 + z ** 2)
# 重力方向となす角度を計算
tilt_angle_x = math.acos(x / gravity)
tilt_angle_y = math.acos(y / gravity)
tilt_angle_z = math.acos(z / gravity)
tilts.append((time, tilt_angle_x, tilt_angle_y, tilt_angle_z))
df_tilt = pd.DataFrame(tilts, columns=["time", "roll", "pitch", "yaw"])
rotated_acc = []
r_x = np.array([
[1, 0, 0],
[0, np.cos(pitch), -np.sin(pitch)],
[0, np.sin(pitch), np.cos(pitch)]
])
r_y = np.array([
[np.cos(roll), 0, np.sin(roll)],
[0, 1, 0],
[-np.sin(roll), 0, np.cos(roll)]
])
r_z = np.array([
[np.cos(yaw), -np.sin(yaw), 0],
[np.sin(yaw), np.cos(yaw), 0],
[0, 0, 1]
])
for data in df_tilt.iterrows():
# 元のベクトル
x = data[1]['x']
y = data[1]['y']
z = data[1]['z']
vec = np.array([x, y, z])
vec = np.dot(r_x, vec)
vec = np.dot(r_y, vec)
vec = np.dot(r_z, vec)
# 回転後の値を格納
rotated_acc.append([
data[1]['time'],
vec[0],
vec[1],
vec[2],
])
df_rotated_acc = pd.DataFrame(rotated_acc, columns=['time', 'x', 'y', 'z'])
fig = plt.figure(figsize=figsize)
plt.title("世界座標での加速度")
plt.xlabel("時間[s]")
plt.ylabel("加速度[m/s^2]")
plt.grid(color='k', linestyle='dotted', linewidth=1, alpha=0.5)
plt.plot(df_rotated_acc["time"], df_rotated_acc["x"], label="x")
plt.plot(df_rotated_acc["time"], df_rotated_acc["y"], label="y")
plt.plot(df_rotated_acc["time"], df_rotated_acc["z"], label="z")
plt.show()
おわりに
この場合、スマホの向いている方向はわかりません.
ジャイロセンサーと磁気センサーを用いるとより良くなります.
よりよい書き方があればぜひ教えてください