概要
一般的に曲線の長さを求めるには区分求積法を使うことが多いと思いますが、実際にプログラミングするにあたっては区分数を一般化しにくい、という問題があります。
ところがベジエ曲線は、区分数を定めることなく、精度をパラメータとして直線近似できるという面白い性質を持っています。近似された直線の長さの累積を曲線の長さとしていいのであれば、その方法を紹介したいと思います。内容としては、以下の wiki ページの作図法の考え方に等しいです。
https://ja.wikipedia.org/wiki/ベジェ曲線
前提知識
点と線の距離の公式
点 $A(x_0,y_0)$ と直線 $l:ax+by+c=0$ の距離 $d$ は
d=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}
証明は他サイトにおまかせします。以下「高校数学の美しい物語」のアドレスです。
https://mathtrain.jp/tentotyokusen
プログラム実装
平面上の3つの点$(x_s,y_s),(x_c,y_c),(x_e,y_e)$を考えます。
$(x_s,y_s)$と$(x_e,y_e)$を結ぶ直線と$(x_c,y_c)$の距離を求めるプログラムを書いてみます。
上の公式をそのまま使ってもいいのですが、$(x_c,y_c)$と$(x_e,y_e)$からあらかじめ$(x_s,y_s)$を引いてやると計算が簡単です。
また現実的には、プログラム中で距離は全て2乗したものとして扱っていくと決めると、sqrt みたいな超越関数を使わなくてすむようになります。なので、距離を返す関数ではなく、距離の2乗を返す関数を定義します。
例えば C++ でプログラムすると以下のようになるでしょう。
template < typename F > F
DiffQ( F xS, F yS, F xC, F yC, F xE, F yE ) {
auto wEx = xE - xS;
auto wEy = yE - yS;
auto wCx = xC - xS;
auto wCy = yC - yS;
if ( wEx == 0 && wEy == 0 ) return wCx * wCx + wCy * wCy;
auto w = wEy * wCx - wEx * wCy;
return w * w / ( wEx * wEx + wEy * wEy );
}
2次ベジエ(Quadratic Bézier curve)の場合
始点を $(x_s,y_s)$、制御点を $(x_c,y_c)$、終点を $(x_e,y_e)$ とする2次ベジエは媒介変数を t とする以下の式で表されます。
\left[ \begin{array}{c} x \\ y \end{array} \right]=\left[ \begin{array}{c} \left( 1-t \right)^{2}x_{s}+2\left( 1-t \right)t\cdot x_{c}+t^{2}x_{e} \\ \left( 1-t \right)^{2}y_{s}+2\left( 1-t \right)t\cdot y_{c}+t^{2}y_{e} \end{array} \right],\; t=0…1
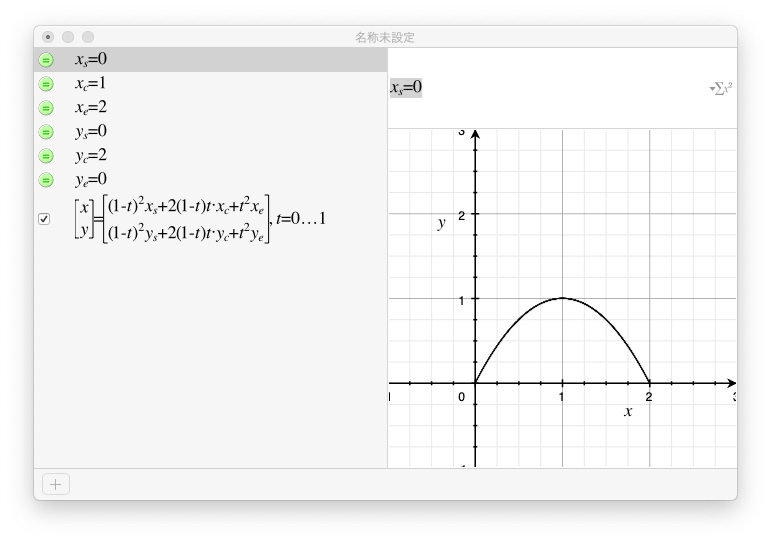
始点を$(0,0)$,制御点を$(1,2)$,終点を$(2,0)$としてGrapher で確認してみます。
曲線が描けていることを確認できました。
ところでここで t が 0.5 の時、
x=\frac{x_s+2x_c+x_e}{4} = 1;
y=\frac{y_s+2y_c+y_e}{4} = 1;
となります。この点は $(x_s,y_s)$ と $(x_e,y_e)$ を結ぶ直線から最も離れた点になります。つまりこの曲線を $(x_s,y_s)$ と $(x_e,y_e)$ を結ぶ直線で近似したら、誤差は1となります。
ベジエ曲線の分割
t = 0.5 の時の点でベジエを2分割することができます。
新しい2つのベジエは以下のようになります。
1つめ
始点:(x_s,y_s)
制御点:(\frac{x_s+x_c}{2},\frac{y_s+y_c}{2})
終点: (\frac{x_s+2x_c+x_e}{4},\frac{y_s+2y_c+y_e}{4})
2つめ
始点:(\frac{x_s+2x_c+x_e}{4},\frac{y_s+2y_c+y_e}{4})
制御点:(\frac{x_c+x_e}{2},\frac{y_c+y_e}{2})
終点: (x_e,y_e)
最初のベジエの $t=0.25$ の点と分割した一つ目の $t = 0.5$ は等しく以下の点になることから分割できることが確認できます。
(\frac{9x_s+6x_c+x_e}{16},\frac{9y_s+6y_c+y_e}{16})
2分割できるのですから、近似した長さは、誤差が小さければ始点と終点の距離、そうでなければ2分割したベジエの距離を足したもの、と再帰的に求めることができます。
プログラム実装
これまでの式をみると、x、yに全て同じ式になってます。なので、パラメータを少なくするために、Coord という型を導入して必要なオペレータを定義します。
template < typename F > struct
Coord {
F x;
F y;
Coord( F x = 0, F y = 0 ) : x( x ), y( y ) {}
F L2NormQ() const { return x * x + y * y; }
};
template < typename F > Coord< F > operator
-( const Coord< F >& l, const Coord< F >& r ) { return Coord< F >( l.x - r.x, l.y - r.y ); }
template < typename F > Coord< F > operator
+( const Coord< F >& l, const Coord< F >& r ) { return Coord< F >( l.x + r.x, l.y + r.y ); }
template < typename F > Coord< F > operator
*( F l, const Coord< F >& r ) { return Coord< F >( l * r.x, l * r.y ); }
template < typename F > Coord< F > operator
/( const Coord< F >& l, F r ) { return Coord< F >( l.x / r, l.y / r ); }
本体です。
template < typename F > F
Bezier2DLength( const Coord< F >& c, const Coord< F >& e ) {
auto wC = ( 2.0 * c + e ) / 4.0;
auto wD = e.L2NormQ();
if ( wD != 0 ) {
auto wN = e.x * wC.y - e.y * wC.x;
if ( wN * wN / wD < 0.5 * 0.5 ) return sqrt( wD );
}
return Bezier2DLength( c / 2.0, wC ) + Bezier2DLength( ( c + e ) / 2.0 - wC, e - wC );
}
template < typename F > F
Bezier2DLength( F xS, F yS, F xC, F yC, F xE, F yE ) {
return Bezier2DLength( Coord< F >( xC - xS, yC - yS ), Coord< F >( xE - xS, yE - yS ) );
}
実行してみます。
cout << Bezier2DLength< double >( 0, 100, 100, 100, 100, 0 ) * 2 << endl;
の結果は
324.372
1/4円弧をちょっと膨らましたような曲線の長さを2倍した値なので、妥当なところっぽいです。3次ではちゃんとやります。
3次ベジエ(Cubic Bézier curve)の場合
考え方は2次と同じです。
始点を $(x_s,y_s)$、制御点1を $(x_1,y_1)$、制御点2を $(x_2,y_2)$、終点を $(x_e,y_e)$ とする3次ベジエは媒介変数を t とする以下の式で表されます。
\left[ \begin{array}{c} x \\ y \end{array} \right]=\left[ \begin{array}{c} \left( 1-t \right)^{3}x_{s}+3\left( 1-t \right)^{2}t\cdot x_{1}+3\left( 1-t \right)t^{2}\cdot x_{2}+t^{3}x_{e} \\ \left( 1-t \right)^{3}y_{s}+3\left( 1-t \right)^{2}t\cdot y_{1}+3\left( 1-t \right)t^{2}\cdot y_{2}+t^{3}y_{e} \end{array} \right],\; t=0…1
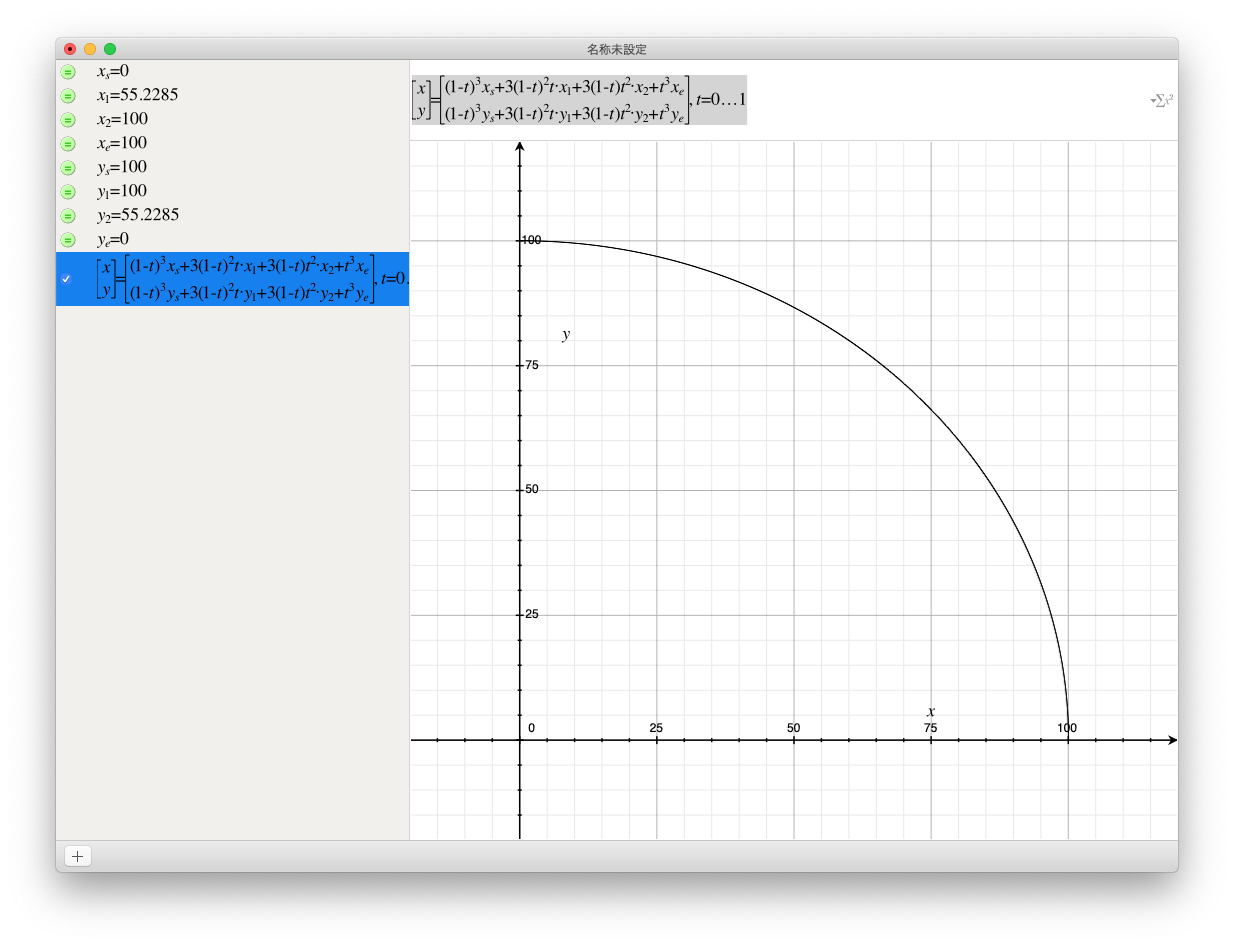
始点を$(0,100)$,制御点1を$(55.2285,100)$,制御点2を$(100,55.2285)$,終点を$(100,0)$としてGrapher で確認してみます。
ただ、3次ベジエは2つの制御点が直線の反対側にあるときは t = 0.5 の点で誤差を求めることができないためその考慮・・無条件に分割する・・が必要です。
ベジエ曲線の分割
2次と同様、t = 0.5 の時の点でベジエを2分割することができます。
新しい2つのベジエは以下のようになります。
1つめ
始点:(x_s,y_s)
制御点1:(\frac{x_s+x_1}{2},\frac{y_s+y_1}{2})
制御点2:(\frac{x_s+2x_1+x_2}{4},\frac{y_s+2y_1+y_2}{4})
終点: (\frac{x_s+3x_1+3x_2+x_e}{8},\frac{y_s+3y_1+3y_2+y_e}{8})
2つめ
始点:(\frac{x_s+3x_1+3x_2+x_e}{8},\frac{y_s+3y_1+3y_2+y_e}{8})
制御点1:(\frac{x_1+2x_2+x_e}{4},\frac{y_1+2y_2+y_e}{4})
制御点2:(\frac{x_2+x_e}{2},\frac{y_2+y_e}{2})
終点: (x_e,y_e)
プログラム実装
これもアイディアは2次と同じですが、2つの制御点が直線の反対側にある場合の処理が入っています。
template < typename F > F
Bezier3DLength( const Coord< F >& c1, const Coord< F >& c2, const Coord< F >& e ) {
auto wC = ( 3.0 * c1 + 3.0 * c2 + e ) / 8.0;
auto wD = e.L2NormQ();
if ( wD != 0 ) {
auto wN1 = e.x * c1.y - e.y * c1.x;
auto wN2 = e.x * c2.y - e.y * c2.x;
if ( wN1 * wN2 >= 0 ) {
auto wN = e.x * wC.y - e.y * wC.x;
if ( wN * wN / wD < 0.5 * 0.5 ) return sqrt( wD );
}
}
return
Bezier3DLength( c1 / 2.0, ( c1 + c1 + c2 ) / 4.0, wC )
+ Bezier3DLength( ( c1 + c2 + c2 + e ) / 4.0 - wC, ( c2 + e ) / 2.0 - wC, e - wC )
;
}
template < typename F > F
Bezier3DLength( F xS, F yS, F xC1, F yC1, F xC2, F yC2, F xE, F yE ) {
return Bezier3DLength( Coord< F >( xC1 - xS, yC1 - yS ), Coord< F >( xC2 - xS, yC2 - yS ), Coord< F >( xE - xS, yE - yS ) );
}
実行してみます。
auto K = ( -24 + sqrt( 24 * 24 + 64 * 9 ) ) / 18;
cout << K * 100 << endl;
cout << Bezier3DLength< double >( 0, 100, K * 100, 100, 100, K * 100, 100, 0 ) * 2 << endl;
の結果は
55.2285
313.801
3次ベジエは1/4円弧をほぼ目ではわからないくらい近似しますので、2倍した値が313.801はいいとこじゃないでしょうか。
ところで、55.2285 という数値が出てきていますが、これは3次ベジエの t=0.5 と原点の距離が100になるように求めたものです。計算式は以下の式の 100 倍です。
( -24 + sqrt( 24 * 24 + 64 * 9 ) ) / 18
なぜコンピュータグラフィックの世界でベジエ曲線がよく使われるのか、わかる気がします。