いろいろやり方はありますが、この記事では一次式の連立方程式を使って考えます。
点と直線の場合
o と p を通る直線に q からおろした垂線の距離の2乗を求めます。
o を p と q からあらかじめ引いておいてやると、計算が楽です。
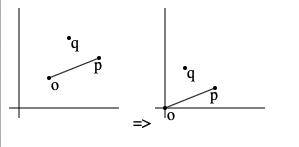
以下のように求められます。
const
_Dist2 = ( px, py, qx, qy ) => {
const num = px * qy - py * qx
return num * num / ( px * px + py * py )
}
const
Dist2 = ( ox, oy, px, py, qx, qy ) => _Dist2( px - ox, py - oy, qx - ox, qy - oy )
注)o と p が同じ場合 0 / 0 になるので NaN を返します。
参考:点と直線の距離公式の3通りの証明@高校数学の美しい物語
点と線分の場合
交点(X,Y)を求めてそれが線分の内に入っているかどうかチェックします。
X,Y は以下のように求められます。
const den = px * px + py * py
const _ = ( py * qy + px * qx ) / den
const X = px * _
const Y = py * _
これの説明は文末につけておきます。
これの X が 0 から px, Y が 0 から py の中に入っていればよさそうです。
ただ、符号の判断が面倒になるので、計算の最初に p が第一象限にあるように鏡像を作ってから考えます。
const
_SegDist2 = ( px, py, qx, qy ) => {
const den = px * px + py * py
if ( den == 0 ) return NaN
if ( px < 0 ) {
px = -px
qx = -qx
}
if ( py < 0 ) {
py = -py
qy = -qy
}
const _ = ( py * qy + px * qx ) / den
const X = px * _
if ( X < 0 || px < X ) return NaN
const Y = py * _
if ( Y < 0 || py < Y ) return NaN
const num = px * qy - py * qx
return num * num / den
}
const
SegDist2 = ( ox, oy, px, py, qx, qy ) => _SegDist2( px - ox, py - oy, qx - ox, qy - oy )
q から op に降ろせる点がない場合 NaN を返しているので、Number.isNaN() で判定してください。
交点の求め方
プログラムっぽく書いてみました。
直線
py
Y = -- X
px
に直行する直線は
px
Y = - -- X + c
py
これが、qx, qy を通るから
px
qy = - -- qx + c
py
すなわち
px px
Y = - -- X + qy + -- qx
py py
なので交点は
py px px
-- X = - -- X + qy + -- qx
px py py
px * ( px * qx + py * qy )
X = --------------------------
px * px + py * py
py * ( px * qx + py * qy )
Y = --------------------------
px * px + py * py