コッホ曲線を Wikipedia で引くとコンピューターによる生成の部分でアフィン変換を使用する方法が紹介されています。ちょっと大変ですね。
HTML の Canvas エレメントを使うと、API がアフィン変換をやってくれちゃうので自分でアフィン変換しなくてもコッホ曲線を描くことができます。Canvas API を使えちゃうプログラミング電卓 SliP でコッホ曲線を描いちゃいましょう!
SliP については以下をご覧ください。
コッホ曲線
詳しい説明は Wikipedia に譲るとして、ここでは次のように考えます。
L のコッホ曲線を描くには:
L が3以下なら長さ L の直線を描く
そうでなければ
L/3のコッホ曲線を描いて60度左に曲がる
L/3の長さのコッホ曲線を描いて120度右に曲がる
L/3の長さのコッホ曲線を描いて60度左に曲がる
L/3の長さのコッホ曲線を描く
プログラミング
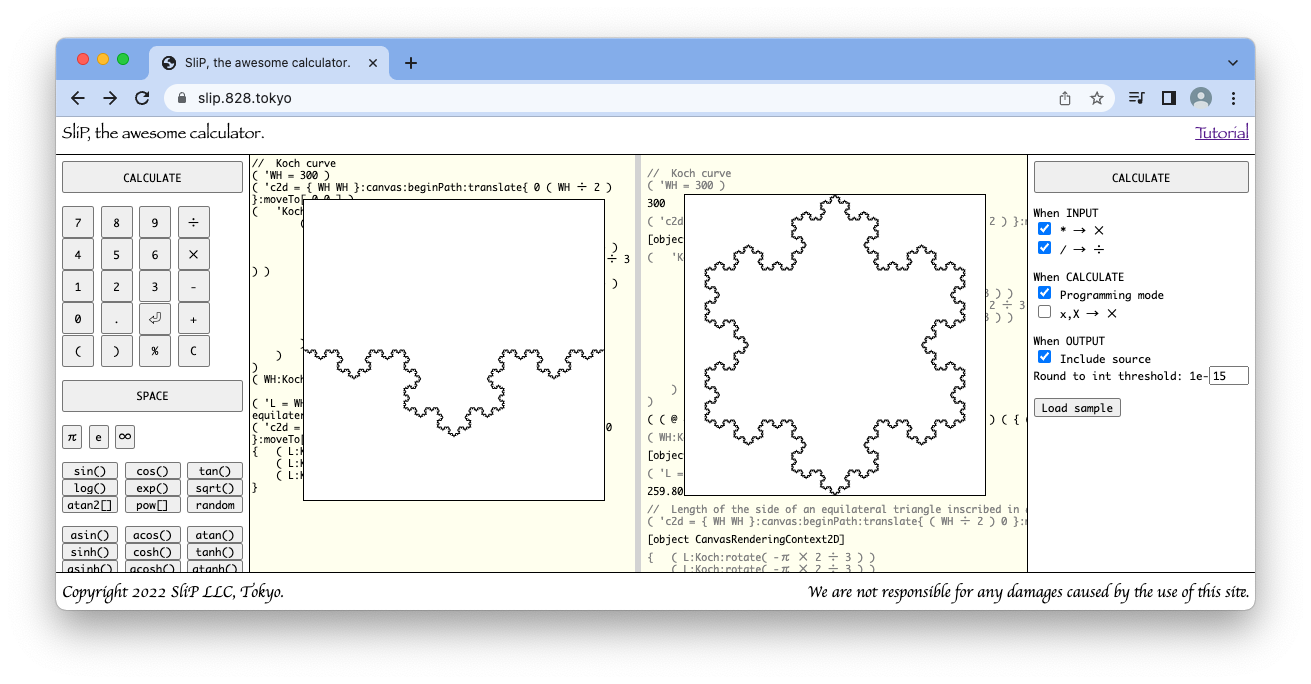
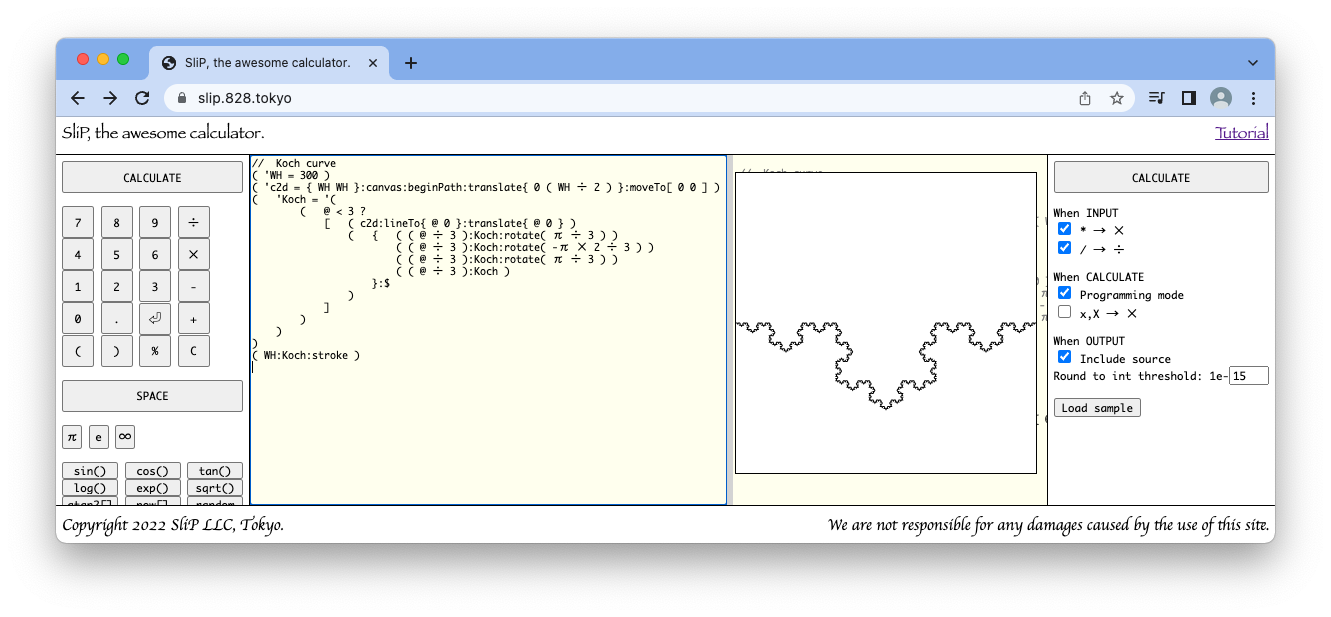
早速プログラミングしてみましょう。上のアドレスのSliPに以下のプログラムを入力してCALCULATEボタンを押してみましょう。この時必ず右のオプションエリアの Programming チェックボックスにチェックを入れておいてください。
( 'WH = 300 )
( 'c2d = { WH WH }:canvas:beginPath:translate{ 0 ( WH ÷ 2 ) }:moveTo[ 0 0 ] )
( 'Koch = '(
( @ < 3 ?
[ ( c2d:lineTo{ @ 0 }:translate{ @ 0 } )
( { ( ( @ ÷ 3 ):Koch:rotate( π ÷ 3 ) )
( ( @ ÷ 3 ):Koch:rotate( -π × 2 ÷ 3 ) )
( ( @ ÷ 3 ):Koch:rotate( π ÷ 3 ) )
( ( @ ÷ 3 ):Koch )
}:$
)
]
)
)
)
( WH:Koch:stroke )
canvasは SliP 上にフローティングの canvas 要素を生成してそのコンテキストを返します。
返されたコンテキストはc2dという名前にアサインされます。
このcanvasを含めこの2行目にある全ての命令は生成されたコンテキストを返します。
beginPathでパスを作る準備をします。
translateで canvas の左端の上下中央に原点を移動して
moveToで原点からパスの始点を置きます。
3行目はKochという関数を定義しています。
@は SliP では引数という意味を持ちます。
?は左辺がNilでなければ(@が3未満)、右辺の最初の式を評価します。
右辺の最初の式はc2dにアサインされたコンテキストに@の長さの線を描画して、原点をその終点に移します。
左辺がNilであれば(@が3以上)右辺の2番目の式を評価します。2番目の式は上の考え方の以下の部分です。
L/3のコッホ曲線を描いて60度左に曲がる
L/3の長さのコッホ曲線を描いて120度右に曲がる
L/3の長さのコッホ曲線を描いて60度左に曲がる
L/3の長さのコッホ曲線を描く
{ 文1 文2 文3 文4 }は評価されると文1 文2 文3 文4の順で評価されそれぞれの値[ 値1 値2 値3 値4 ]を返します。ここでは[ コンテキスト コンテキスト コンテキスト コンテキスト ]と返ってくるので、:$で最後の一つだけ取り出します。
( WH:Koch:stroke )はいよいよKochの実行です。WHには300という値が入っています。strokeは実際に線を描きます。
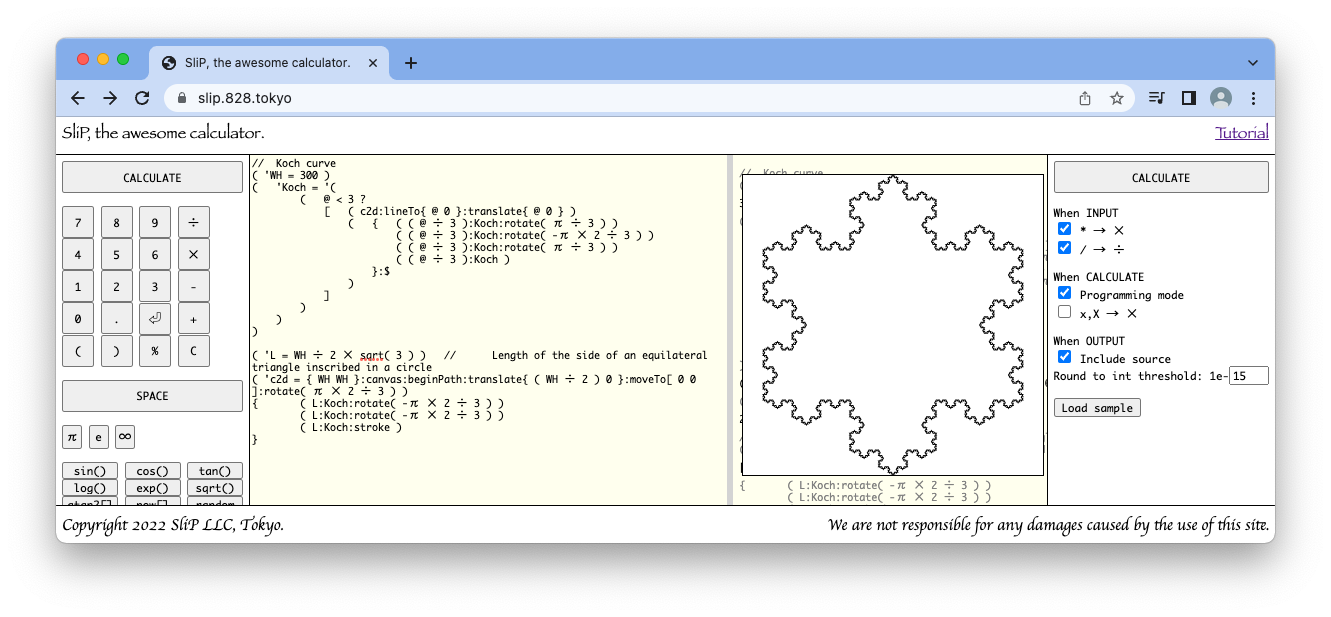
コッホ雪片
同一の長さのコッホ曲線を3つ描くとコッホ雪片という図形になります。
( 'L = WH ÷ 2 × sqrt( 3 ) ) // Length of the side of an equilateral triangle inscribed in a circle
( 'c2d = { WH WH }:canvas:beginPath:translate{ ( WH ÷ 2 ) 0 }:moveTo[ 0 0 ]:rotate( π × 2 ÷ 3 ) )
{ ( L:Koch:rotate( -π × 2 ÷ 3 ) )
( L:Koch:rotate( -π × 2 ÷ 3 ) )
( L:Koch:stroke )
}
canvas を作って、上端の左右中央に原点を移動して始点を移し右に120度曲がり
コッホ曲線を引いて左に120度曲がり、
コッホ曲線を引いて左に120度曲がり、
コッホ曲線を引いて線を描画です。
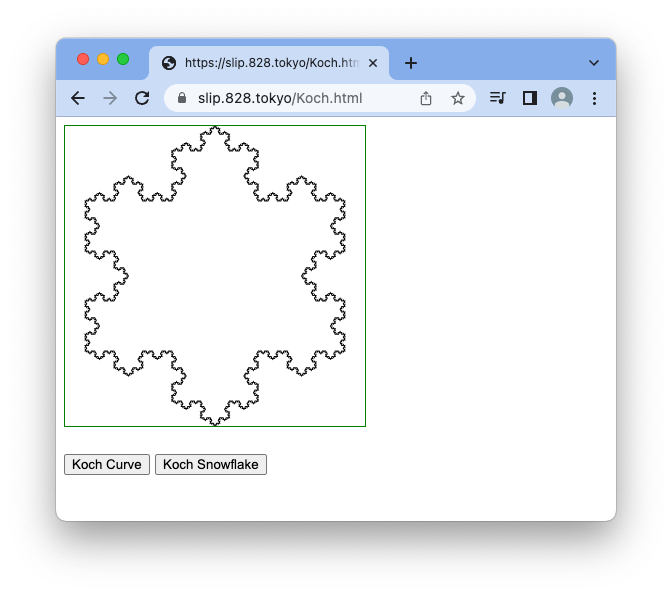
JavaScript で
HTML + JavaScript も用意してみました。
ここにアクセスしていただいてもいいですし、下のソースを拡張子htmlのファイルにしてブラウザに読ませればいけると思います。
<canvas id=CANVAS width=300 height=300 style="border: 1px solid green"></canvas><br>
<br>
<input type=button id=CURVE value="Koch Curve" >
<input type=button id=SNOWFLAKE value="Koch Snowflake" >
<script type=module>
const
c2d = CANVAS.getContext( '2d' )
const
Koch = _ => _ < 3
? ( c2d.lineTo( _, 0 )
, c2d.translate( _, 0 )
)
: ( Koch( _ / 3 )
, c2d.rotate( Math.PI / 3 )
, Koch( _ / 3 )
, c2d.rotate( - Math.PI * 2 / 3 )
, Koch( _ / 3 )
, c2d.rotate( Math.PI / 3 )
, Koch( _ / 3 )
)
CURVE.onclick = ev => (
c2d.clearRect( 0, 0, CANVAS.width, CANVAS.height )
, c2d.save()
, c2d.beginPath()
, c2d.translate( 0, CANVAS.height / 2 )
, c2d.moveTo( 0, 0 )
, Koch( CANVAS.width )
, c2d.stroke()
, c2d.restore()
)
SNOWFLAKE.onclick = ev => {
c2d.clearRect( 0, 0, CANVAS.width, CANVAS.height )
c2d.save()
const _ = CANVAS.width / 2 * Math.sqrt( 3 ) // Length of the side of an equilateral triangle inscribed in a circle
c2d.beginPath()
c2d.translate( CANVAS.width / 2, 0 )
c2d.moveTo( 0, 0 )
c2d.rotate( Math.PI * 2 / 3 )
Koch( _ )
c2d.rotate( -Math.PI * 2 / 3 )
Koch( _ )
c2d.rotate( -Math.PI * 2 / 3 )
Koch( _ )
c2d.stroke()
c2d.restore()
}
</script>
最後に
ここまでお読みいただきありがとうございました!